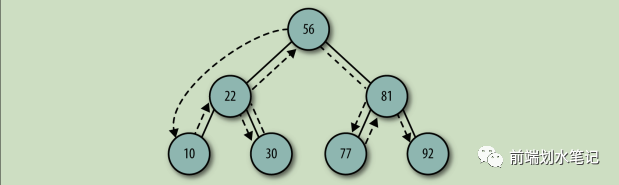
一、简介和应用 二叉树是一种重要的非线性数据结构，每个节点最多有两个子节点，分别称为左子节点和右子节点。它在计算机科学中有广泛的应用，是许多高级数据结构的基础。

‌应用场景‌：

1.数据库索引（如B树、B+树） 2.文件系统目录结构 3.表达式树（用于编译器实现） 4.决策树（机器学习算法） 5.游戏AI中的决策系统 6.哈夫曼编码（数据压缩） 二叉树特别适合需要快速查找、插入和删除操作的场景，它的平均时间复杂度通常是O(log n)。

二、特点 ‌特点‌： 1.层次结构：数据以层次方式组织 2.递归性质：每个子树也是二叉树 3.灵活大小：可以动态增长或缩小 4.多种遍历方式：前序、中序、后序遍历 5.高效搜索：在平衡二叉树中搜索效率高

三、实现步骤解析 1‌.定义节点结构‌：创建包含数据、左指针和右指针的结构体 ‌2.初始化树‌：创建根节点作为树的起点 ‌3.实现基本操作‌： 4‌.实现遍历功能‌： 四、完整代码和注释

#include<iostream>
using namespACe std;

// 定义二叉树节点结构体
struct treenode{
    int data=0;            // 节点存储的数据，默认为0
    treenode* left=nullptr;  // 左子节点指针，默认为空
    treenode* right=nullptr; // 右子节点指针，默认为空

    // 默认构造函数
    treenode() {}

    // 带参数的构造函数，可以指定父节点和位置
    treenode(int d, treenode* h, bool children){
        data = d;
        if (!children)      // 如果是左子节点
            h->left = this;  // 父节点的左指针指向当前节点
        else                // 如果是右子节点
            h->right = this; // 父节点的右指针指向当前节点
    }

    // 只带数据的构造函数
    treenode(int d){
        data = d;
    }
};

// 定义二叉树类
class tree{
public:
    treenode* root; // 根节点指针

    // 构造函数，初始化根节点
    tree(){
        root = new treenode;
    }

    // 在指定父节点的指定位置添加新节点
    void add(treenode* parent, bool children, int data){
        treenode* newnode = new treenode(data, parent, children);
    }

    // 递归添加节点，自动找到合适位置
    void add(treenode* node, int data){
        if (!node->left){    // 如果左子节点为空
            node->left = new treenode(data); // 添加到左子节点
            return;
        }
        if (!node->right){   // 如果右子节点为空
            node->right = new treenode(data); // 添加到右子节点
            return;
        }
        add(node->left, data); // 递归尝试在左子树添加
    }

    // 删除指定父节点的指定子节点
    void remove(treenode* parent, bool children){
        if (!children)       // 如果是左子节点
            parent->left = nullptr;  // 置空左指针
        else                 // 如果是右子节点
            parent->right = nullptr; // 置空右指针
        // 注意：这里应该释放被删除节点的内存
    }

    // 修改指定节点的数据
    void change(treenode* node, int data){
        node->data = data;   // 直接修改数据
    }

    // 递归查找包含指定数据的节点
    treenode* find(int data, treenode* root){
        if (!root)           // 如果当前节点为空
            return nullptr;   // 返回空指针
        if (root->data == data) // 如果找到数据
            return root;      // 返回当前节点
        treenode* ret;
        ret = find(data, root->left);  // 在左子树中查找
        if (ret)             // 如果在左子树中找到
            return ret;      // 返回找到的节点
        ret = find(data, root->right); // 在右子树中查找
        if (ret)             // 如果在右子树中找到
            return ret;      // 返回找到的节点
        return nullptr;      // 没找到返回空指针
    }

    // 前序遍历（根-左-右）
    void printpre(treenode* node){
        if (!node)           // 如果节点为空
            return;          // 返回
        cout << node->data << " "; // 先访问根节点
        printpre(node->left);      // 再遍历左子树
        printpre(node->right);     // 最后遍历右子树
    }

    // 中序遍历（左-根-右）
    void printmid(treenode* node){
        if (!node)           // 如果节点为空
            return;          // 返回
        printmid(node->left);      // 先遍历左子树
        cout << node->data << " "; // 再访问根节点
        printmid(node->right);     // 最后遍历右子树
    }

    // 后序遍历（左-右-根）
    void printpost(treenode* node){
        if (!node)           // 如果节点为空
            return;          // 返回
        printpost(node->left);     // 先遍历左子树
        printpost(node->right);    // 再遍历右子树
        cout << node->data << " "; // 最后访问根节点
    }
};

五、总结 二叉树是计算机科学中最重要的数据结构之一，理解它的原理和实现对于学习更高级的数据结构和算法至关重要。本文通过一个完整的C++实现，展示了二叉树的基本操作和三种遍历方式。对于初学者来说，掌握二叉树将为学习堆、平衡二叉树、图等更复杂的数据结构奠定坚实基础。 转自：二叉树入门指南：从零开始理解树形数据结构