树是一种数据结构,该章节讨论二叉树(二叉树的每个节点的子节点不允许超过两个),二叉树中有又分为完全二叉树和不完全二叉树.....
不在本章节赘述相关概念,感兴趣可以去查阅《数据结构》。
你将会获得:
1.如何使用js实现二叉查找树。
2.学会前、中、后序遍历。
3.了解相关实现原理
阅读时长>5min,可选择直接调试代码
特点
二叉查找树中序遍历后,得到的增序的排列方式。 预览
以下封装的二叉查找树,包含了查找方法
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
}
Node.prototype.show = function() {
return this.data;
}
function BST() {
this.root = null;
}
BST.prototype.insert = function (data) {
var n = new Node(data, null, null);
if (this.root == null) {
this.root = n;
} else {
var current = this.root;
var parent;
while (true) {
parent = current;
if (data < current.data) {
current = current.left;
if (current == null) {
parent.left = n;
break;
}
} else {
current = current.right;
if (current == null) {
parent.right = n;
break;
}
}
}
}
}
BST.prototype.inOrder = function(node) {
// 中序遍历
if (!(node == null)) {
inOrder(node.left);
console.log(node.show() + "");
inOrder(node.right);
}
}
BST.prototype.preOrder = function(node) {
// 先序
if (!(node == null)) {
console.log(node.show() + "");
preOrder(node.left);
preOrder(node.right);
}
}
BST.prototype.postOrder = function(node) {
// 先序
if (!(node == null)) {
postOrder(node.left);
postOrder(node.right);
console.log(node.show() + "");
}
}
// 查找最小值
BST.prototype.getMin = function() {
var current = this.root;
while (current.left !== null) {
current = current.left;
}
return current.data;
}
// 查找最大值
BST.prototype.getMax = function() {
var current = this.root;
while (current.right !== null) {
current = current.right;
}
return current.data;
}
// 查找给定值
BST.prototype.find = function(data) {
var current = this.root;
while (current != null) {
if (current.data == data) {
return current;
} else if (data < current.data) {
current = current.left;
} else if (data > current.data) {
current = current.right;
}
}
return null;
}
BST.prototype.remove = function(data) {
this.root = this.removeNode(this.root, data);
console.log(this.root,1)
}
BST.prototype.removeNode = function(node, data) {
if (node == null) {
return null;
}
if (data == node.data) {
// 没有子节点的节点
if (node.left == null && node.right == null) {
return null;
}
// 没有左子节点的节点
if (node.left == null) {
return node.right;
}
// 没有右子节点的节点
if (node.right == null) {
return node.left;
}
// 查找最小节点
let getSmallest = function(node) {
if (node.left === null && node.right == null) {
return node;
}
if (node.left != null) {
return node.left;
}
if (node.right !== null) {
return getSmallest(node.right);
}
}
// 有两个子节点的节点
var tempNode = getSmallest(node.right);
node.data = tempNode.data;
node.right = this.removeNode(node.right, tempNode.data);
return node;
} else if (data < node.data) {
node.left = this.removeNode(node.left, data);
return node;
} else {
node.right = this.removeNode(node.right, data);
return node;
}
}中序排列
var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);
console.log("Inorder traversal: ");
nums.inOrder(nums.root);
> Inorder traversal:
> 3 16 22 23 37 45 99 // 增序1.实现
二叉查找树是一种特殊的二叉树,_相对较小的值保存在左节点中,较大的值保存在右节点_。这一特性使得查找效率很高,对于数值型和非数值型的数据,比如单词和字符串都是如此。
// 节点
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
this.show = show;
}
Node.prototype.show = function() {
return this.data;
}1.1创建BST类
BST 先要有一个 insert() 方法,用来向树中加入新节点。
首先要创建一个 Node 对象,将数据传入该对象保存。其次检查 BST 是否有根节点,如果没有,那么这是棵新树,该节点就是根节点,这个方法 到此也就完成了;否则,进入下一步。如果待插入节点不是根节点,那么就需要准备遍历 BST,找到插入的适当位置。该过程类 似于遍历链表。用一个变量存储当前节点,一层层地遍历 BST。进入 BST 以后,下一步就要决定将节点放在哪个地方。找到正确的插入点时,会跳出循 环。查找正确插入点的算法如下。
(1) 设根节点为当前节点。 (2) 如果待插入节点保存的数据小于当前节点,则设新的当前节点为原节点的左节点;反 之,执行第 4 步。 (3) 如果当前节点的左节点为 null,就将新的节点插入这个位置,退出循环;反之,继续 执行下一次循环。 (4) 设新的当前节点为原节点的右节点。 (5) 如果当前节点的右节点为 null,就将新的节点插入这个位置,退出循环;反之,继续 执行下一次循环。
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
}
Node.prototype.show = function() {
return this.data;
}
function BST() {
this.root = null;
}
BST.prototype.insert = function (data) {
var n = new Node(data, null, null);
if (this.root == null) {
this.root = n;
} else {
var current = this.root;
var parent;
while (true) {
parent = current;
if (data < current.data) {
current = current.left;
if (current == null) {
parent.left = n;
break;
}
} else {
current = current.right;
if (current == null) {
parent.right = n;
break;
}
}
}
}
}以上是最主要的,二叉查找树的js实现,其他方法简单描述一下
中序:就是先访问左子节点-->根节点-->右子节点
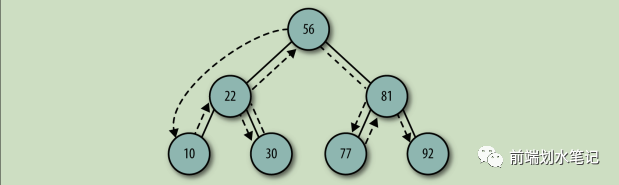
先序: 就是先访问根节点再访问子节点
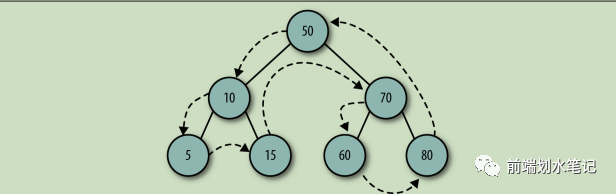
后序:最后访问根节点
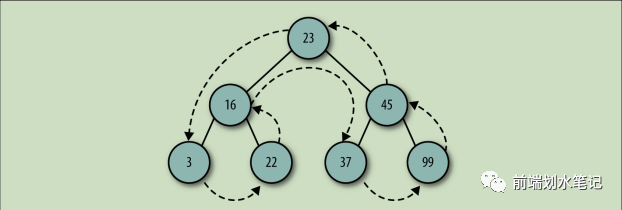
删除二叉树节点:
删除节点主要分为,叶子节点,有左节点,有右节点,有两个子节点;
思路就是:
找到要删除节点,判断是否含有子节点。
如果没有子节点,便将该节点的值置为null。
2.1 有左/右节点,被删节点指向子节点。
2.2 含左右节点:
- (1)查找待删节点的左子树的最大值
- (2)查找待删节点的右子树的最小值
将待删节点的值替换成以上(1)/(2)的值
以下选的是(2)方案
BST.prototype.remove = function(data) {
// 最后改变根节点值
this.root = this.removeNode(this.root, data);
}
// 返回的是node类型
BST.prototype.removeNode = function(node, data) {
if (node == null) {
return null;
}
if (data == node.data) {
// 没有子节点的节点
if (node.left == null && node.right == null) {
return null;
}
// 没有左子节点的节点
if (node.left == null) {
return node.right;
}
// 没有右子节点的节点
if (node.right == null) {
return node.left;
}
// 查找最小节点
let getSmallest = function(node) {
if (node.left === null && node.right == null) {
return node;
}
if (node.left != null) {
return node.left;
}
if (node.right !== null) {
return getSmallest(node.right);
}
}
// 有两个子节点的节点
var tempNode = getSmallest(node.right);
node.data = tempNode.data;
// 处理待删节点的右子树
node.right = this.removeNode(node.right, tempNode.data);
return node;
} else if (data < node.data) {
node.left = this.removeNode(node.left, data);
return node;
} else {
node.right = this.removeNode(node.right, data);
return node;
}
}欢迎关注《前端划水笔记》