原文链接：https://note.noxussj.top/?source=helloworld

---

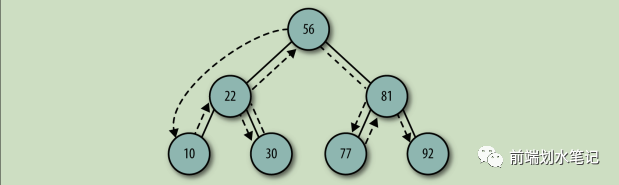
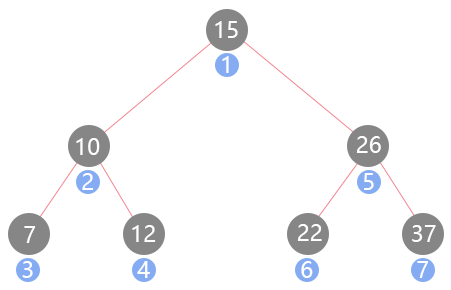
什么是二叉树？

树中每个节点最多只能有两个子节点，在 JavaScript 中一般都是通过 Object 来模拟二叉树。

常用操作

• 前序遍历
• 中序遍历
• 后序遍历

前序遍历

根左右。

口诀：

1. 访问根节点
2. 对根节点的左子树进行前序遍历
3. 对根节点的右子树进行前序遍历

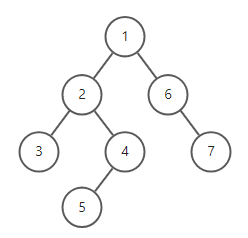
通过递归方式实现

function preorder(root) {
    if (!root) return

    console.log(root.val)
    preorder(root.left)
    preorder(root.right)
}

通过迭代方式实现

function preorder(root) {
    if (!root) return

    const stack = [root]

    while (stack.length) {
        const n = stack.pop()

        console.log(n)
        if (n.right) stack.push(n.right)
        if (n.left) stack.push(n.left)
    }
}

中序遍历

左根右。

口诀：

1. 对根节点的左子树进行中序遍历
2. 访问根节点
3. 对根节点的右子树进行中序遍历

通过递归方式实现

function inorder(root) {
    if (!root) return

    inorder(root.left)
    console.log(root.val)
    inorder(root.right)
}javascript

通过迭代方式实现

function inorder(root) {
    if (!root) return

    const stack = [root]

    while (stack.length) {
        const n = stack.pop()

        console.log(n)
        if (n.right) stack.push(n.right)
        if (n.left) stack.push(n.left)
    }
}

后序遍历

左右根。

口诀：

1. 对根节点的左子树进行后序遍历
2. 对根节点的右子树进行后序遍历
3. 访问根节点

通过递归方式实现

function postorder(root) {
    if (!root) return

    postorder(root.left)
    postorder(root.right)
    console.log(root.val)
}

通过迭代方式实现

function postorder(root) {
    if (!root) return

    const outputStack = []
    const stack = [root]

    while (stack.length) {
        const n = stack.pop()

        outputStack.push(n)
        if (n.left) stack.push(n.left)
        if (n.right) stack.push(n.right)
    }

    while (outputStack.length) {
        const n = outputStack.pop()
        console.log(n.val)
    }
}