一、定义
二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree) 。
二、特性
- 在二叉树的第i层上至多有2^(i-1)个结点(i>0)
- 深度为k的二叉树至多有2^k - 1个结点(k>0)
- 对于任意一棵二叉树,如果其叶结点数为N0,而度数为2的结点总数为N2,则N0=N2+1
- 具有n个结点的完全二叉树的深度必为 log2(n+1)
- 对完全二叉树,若从上至下、从左至右编号,则编号为i 的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2(i=1 时为根,除外)
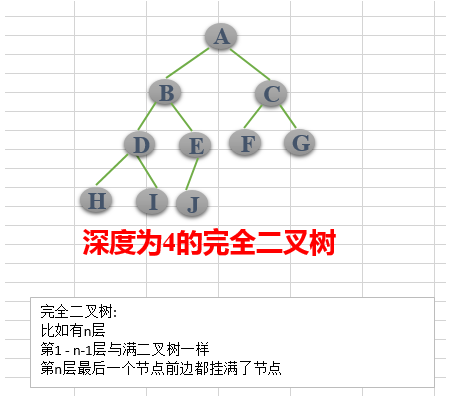
- 完全二叉树
若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。
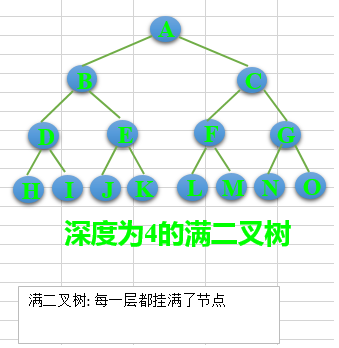
- 满二叉树
除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。
三、遍历
树的遍历是树的一种重要的运算。我们把依次对树中每个结点访问一次且仅访问一次的运算称为_遍历(traversal)_。那么树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先一般用递归,广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。
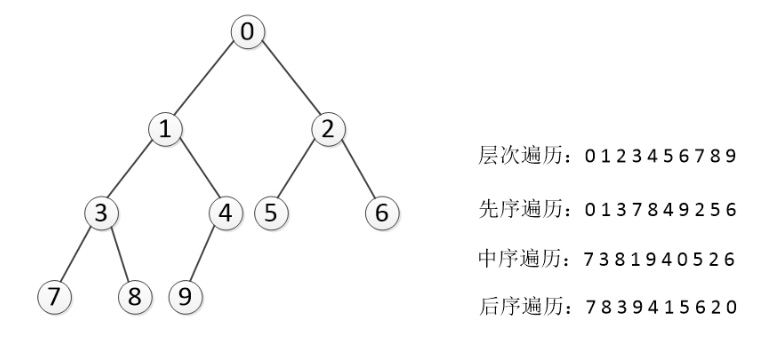
1.深度优先遍历
对于一颗二叉树,_深度优先搜索(Depth First Search)_是沿着树的深度遍历树的节点,尽可能深的搜索树的分支。深度优先遍历有重要的三种方式,这三种方式常被用于访问树的节点,它们之间的不同在于访问每个节点的次序不同。
- 先序遍历(preorder)
先序遍历中,我们先访问根节点,然后递归使用先序遍历访问左子树,再递归使用先序遍历访问右子树。
根节点->左子树->右子树
- 中序遍历(inorder)
中序遍历中,我们递归使用中序遍历访问左子树,然后访问根节点,最后再递归使用中序遍历访问右子树。
左子树->根节点->右子树
- 后序遍历(postorder)
后序遍历中,我们先递归使用后序遍历访问左子树和右子树,最后访问根节点。
左子树->右子树->根节点
2.广度优先遍历(层次遍历)
从树的根开始,从上到下、从左到右遍历整个树的节点。
四、PHP的实现
节点实现:
<?php
/**
* 节点实现
*/
class Node
{
/**
* 节点值
* @var
*/
public $elem;
/**
* 左孩子
* @var
*/
public $lchild;
/**
* 右孩子
* @var
*/
public $rchild;
/**
* Node constructor.
* @param $item
*/
public function __construct($elem = -1,$lchild = null,$rchild = null)
{
$this->elen = $elem;
$this->lchild = $lchild;
$this->rchild = $rchild;
}
}
树的实现:
<?php
/**
* 二叉树基本操作
* 1.add(elem) 添加节点
* 2.breadth() 层次遍历
* 3.preorder(node) 先序遍历
* 4.inorder(node) 中序遍历
* 5.postorder(node) 后序遍历
*/
class Tree
{
/**
* 根节点
* @var null
*/
public $root;
/**
* Tree constructor.
* @param null $root
*/
public function __construct($root = null)
{
$this->root = $root;
}
/**
* 节点添加
* @param $elem
* @return void
*/
public function add($elem)
{
$node = new Node($elem);
//若树是空的,则队根节点赋值
if(is_null($this->root)){
$this->root = $node;
return;
}
$queue = [];
array_push($queue,$this->root);
//对已有节点进行层次遍历
while($queue){
//出队
$cur = array_shift($queue);
//左孩子处理
if(is_null($cur->lchild)){
$cur->lchild = $node;
return;
}else{
array_push($queue,$cur->lchild);
}
//右孩子处理
if(is_null($cur->rchild)){
$cur->rchild = $node;
return;
}else{
array_push($queue,$cur->rchild);
}
}
}
/**
* 层次遍历
* 从根开始,从上到下、从左到右遍历整个树的节点
*/
public function breadth()
{
if(is_null($this->root)){
return;
}
$queue = [$this->root];
while ($queue){
$cur = array_shift($queue);
echo $cur->elem . '<br />';
if(!is_null($cur->lchild)){
array_push($queue,$cur->lchild);
}
if(!is_null($cur->rchild)){
array_push($queue,$cur->rchild);
}
}
}
/**
* 先序遍历
* 根节点->左子树->右子树
* @param Node $node
*/
public function preorder($node)
{
if(is_null($node)){
return;
}
echo $node->elem . '<br />';
$this->preorder($node->lchild);
$this->preorder($node->rchild);
}
/**
* 中序遍历
* 左子树->根节点->右子树
* @param $node
*/
public function inorder($node)
{
if(is_null($node)){
return;
}
$this->inorder($node->lchild);
echo $node->elem . '<br />';
$this->inorder($node->rchild);
}
/**
* 后序遍历
* 左子树->右子树->根节点
* @param $node
*/
public function postorder($node)
{
if(is_null($node)){
return;
}
$this->postorder($node->lchild);
$this->postorder($node->rchild);
echo $node->elem . '<br />';
}
}
$tree = new Tree();
$tree->add(0);
$tree->add(1);
$tree->add(2);
$tree->add(3);
$tree->add(4);
$tree->add(5);
$tree->add(6);
$tree->add(7);
$tree->add(8);
$tree->add(9);
$tree->breadth();
//$tree->preorder($tree->root);
//$tree->inorder($tree->root);
//$tree->postorder($tree->root);













