手把手教你实现二叉树：从代码注释到实战应用

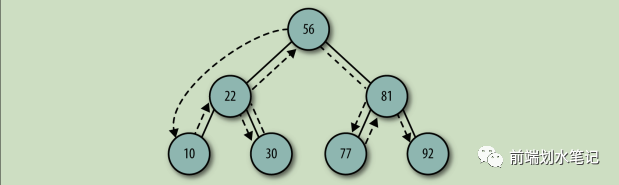
一、简介和应用

二叉树是一种经典的数据结构，它由节点组成，每个节点最多有两个子节点（左子节点和右子节点）。这种结构因其简洁性和高效性被广泛应用于算法设计、数据存储与检索等领域。例如，文件系统目录结构、搜索算法（如二叉搜索树）以及表达式解析树等场景都离不开二叉树。对于编程新手来说，理解二叉树的基本原理和实现方式，是掌握数据结构与算法的重要一步。

二、特点和注意事项

特点：

二叉树通过分层结构组织数据，支持快速插入、查找和删除操作。

遍历方式多样（前序、中序、后序），便于不同场景的数据处理。

递归实现简洁，但需注意递归深度以避免栈溢出。
注意事项：

需确保树的平衡性（如通过平衡树算法），避免因节点分布不均导致性能下降。

删除节点时需处理子节点指针，防止内存泄漏或指针悬空。

理解递归逻辑，避免因递归调用层次过多导致程序崩溃。

三、实现步骤

定义节点结构：使用 treenode 结构体存储数据、左右子节点指针。
构建树类：通过 tree 类封装树的操作，初始化根节点。
添加节点：

add(parent, children, data)：指定父节点及子节点位置（左/右）添加新节点。

add(node, data)：递归查找空子节点位置插入。
删除节点：通过 remove(parent, children) 指定父节点和子节点位置（左/右）删除。
数据修改与查找：

change(node, data)：直接修改节点数据。

find(data, root)：递归遍历查找目标数据节点。
遍历方法：实现前序、中序、后序三种递归遍历方式，输出节点数据。

四、代码与注释

#include <iostream>
using namespace std;

// 定义二叉树节点结构体
struct treenode {
// 节点数据
int data = 0;
// 左右子节点指针
treenode* left = nullptr;
treenode* right = nullptr;

// 默认构造函数
treenode() {}

// 带参数构造函数（用于指定父节点和位置添加子节点）
treenode(int d, treenode* h, bool children) {
data = d; // 设置数据
if (!children) // 如果为左子节点
h->left = this; // 将当前节点挂载到父节点左侧
else // 如果为右子节点
h->right = this; // 挂载到右侧
}

// 仅数据初始化的构造函数
treenode(int d) {
data = d;
}
};

class tree {
public:
treenode* root; // 根节点指针

// 树构造函数，初始化根节点
tree() {
root = new treenode; // 创建根节点
}

// 在指定父节点添加子节点（左/右）
void add(treenode* parent, bool children, int data) {
treenode* newnode = new treenode(data, parent, children);
}

// 递归查找空位置添加节点
void add(treenode* node, int data) {
if (!node->left) { // 若左子节点为空
node->left = new treenode(data); // 添加左节点
return;
}
if (!node->right) { // 若右子节点为空
node->right = new treenode(data); // 添加右节点
return;
}
add(node->left, data); // 递归查找左子树
add(node->right, data); // 递归查找右子树
}

// 删除指定父节点的左/右子节点
void remove(treenode* parent, bool children) {
if (!children) // 删除左子节点
parent->left = nullptr;
else // 删除右子节点
parent->right = nullptr;
}

// 修改节点数据
void change(treenode* node, int data) {
node->data = data;
}

// 递归查找数据节点
treenode* find(int data, treenode* root) {
if (!root) // 若节点为空，终止递归
return nullptr;
if (root->data == data) // 找到目标数据
return root;
treenode* ret;
ret = find(data, root->left); // 递归查找左子树
if (ret) return ret; // 若找到，直接返回
ret = find(data, root->right); // 递归查找右子树
if (ret) return ret;
return nullptr; // 未找到，返回空
}

// 前序遍历（根-左-右）
void printpre(treenode* node) {
if (!node) return;
cout << node->data << " ";
printpre(node->left);
printpre(node->right);
}

// 中序遍历（左-根-右）
void printmid(treenode* node) {
if (!node) return;
printmid(node->left);
cout << node->data << " ";
printmid(node->right);
}

// 后序遍历（左-右-根）
void printpost(treenode* node) {
if (!node) return;
printpost(node->left);
printpost(node->right);
cout << node->data << " ";
}
};