树与二叉树 - HelloWorld开发者社区

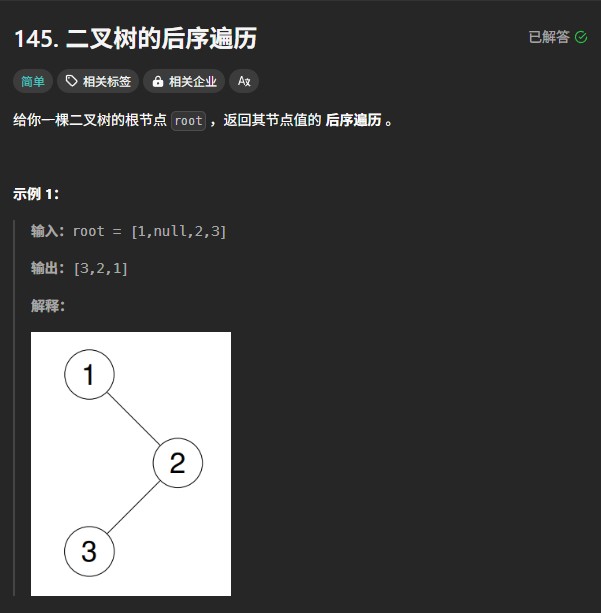
二叉树层次建树

二叉树（Binary Tree）是由有限个结点组成的集合，它或者为空集合，或者仅含一个根结点，或者由一个根结点和两棵互不相交的左、右子树组成。 树为空即根节点为空。 二叉树的基本形态如下图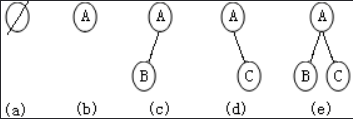：树与二叉树 a：空的二叉树，tree=NULL。 b：只有空节点的二叉树，tree=A。 c：只有左子树的二叉树。 d：只有右子树的二叉树。 e：左右子树都存在。分为完全二叉树和满二叉树。 ::: tip 满二叉树：除叶子节点外，其余节点都是满的。 完全二叉树：除末尾的叶子节点外，其余节点都是满的（其余节点必须连续放满）。完全二叉树节点编号时是连续的。 ::: ::: warning 二叉树编号时从1开始。孩子节点的序号/2=父节点的序号。 :::

二叉树的单一个体如下图所示，结构体是由该单一个体确定的。树与二叉树 typedef struct BiTNode { char data; //数据 struct BiTNode* lchild; //左子树 struct BiTNode* rchild; //右子树 }; 树定义与二叉树定义稍有区别。首先，树不能是空树（更正：树可以为空（0个节点））却可以有空二叉树。其次，一般树的子树的不分次序，而二叉树的子树却分左、右子树，即使在仅有一棵子树的情况下也要指明是左子树还是右子树。最后，一般树中结点的度(子树数目)可以大于2，但二叉树中结点的度均不超过2。

辅助队列是链表实现的，没有头节点，起始时头指针和尾指针都指向第一个节点，此时辅助队列为空，即树为空。 二叉树层次建树代码实现：结构体类型声明放在function.h头文件中。 function.h：

#include <stdio.h>
#include <stdlib.h>

typedef char BiElemType;
//树的队列
typedef struct BiTNode
{
    BiElemType data;
    struct BiTNode* lchild;
    struct BiTNode* rchild;
}BiTNode, * BiTree;

//辅助队列使用，队列是链表实现的
typedef struct tag
{
    BiTree p;  //树的某一结点的地址，需要使用指针
    struct tag* pnext;  //链表中的next指针，用于指向下一个节点
}tag_t, * ptag_t;

main.cpp：

#include "function.h"

int main()
{
    BiTree pnew;  //pnew指向树申请的新节点的指针
    BiTree tree = NULL;  //tree指向树根（第一个节点，即根节点），用来代表树，树根需要初始化为NULL
    char data;  //要输入的元素（abcdefghij）
    ptag_t phead = NULL, ptail = NULL;  //队列头指针和队列尾指针初始化为NULL
    ptag_t list_pnew = NULL, pcur = NULL;  //辅助队列中list_pnew和树中pnew对应，pcur指向当前读进树中的节点的父亲节点
    while (scanf("%c", &data))  //把每一个字符作为树的节点存入树中
    {
        if (data == '\n')
        {
            break;  //读取输入内容时，末尾的\n不放入树
        }
        pnew = (BiTree)calloc(1, sizeof(BiTNode));  //每读入一个数据，都要开辟节点
        //使用malloc开辟节点时，读取的字符存在data中，但是左右孩子需要初始化为NULL，比较麻烦
        //calloc申请空间的大小是两个参数的乘积，calloc申请空间后会先将空间初始化为0
        pnew->data = data;  //将读进来的数据存进申请树的结构体的data中
        list_pnew = (ptag_t)calloc(1, sizeof(tag_t));  //该节点的地址放入辅助队列，给队列节点申请空间
        list_pnew->p = pnew;  //队列结构体中p存放的是树中对应结点pnew的地址
        //判断是否为树的第一个节点
        if (NULL == tree)  //当tree=NULL时，树为空，即此时树中开辟的节点是根节点，辅助队列中申请的是第一个节点
        {
            tree = pnew;  //树为空时，tree指向读入的第一个节点（根节点），其余字符读进来时tree不为空
            phead = ptail = list_pnew;  //起始时辅助队列中队列头和队列尾都指向第一个节点a
            pcur = list_pnew;  //pcur指向读入节点的父亲节点，只有一个根节点a时，pcur指向根节点a
        }
        else {
            //元素b先入队列
            ptail->pnext = list_pnew;  //读入新元素（b）的地址放在队列尾指针的pnext域
            ptail = list_pnew;  //新读入的元素b变为队列新的尾部，
            //节点b放入树中
            if (NULL == pcur->p->lchild)
            {
                pcur->p->lchild = pnew;  //当pcur指向的节点a的左孩子为NULL时，a的左孩子指向新节点b
            }
            else if (NULL == pcur->p->rchild)  //读入第三个元素c时
            {
                pcur->p->rchild = pnew;  //当pcur指向的节点a的左孩子不为NULL右孩子为NULL时，a的又孩子指向新节点c
                pcur = pcur->pnext;  //pcur->p即节点a的左右孩子都已经放了节点后，当前节点放满，pcur指向下一个节点b
            }
        }
    }
    return 0;
}

层次建树代码重写：

#include <stdio.h>
#include <stdlib.h>

typedef char Elemtype;
typedef struct Node
{
    Elemtype data;
    struct Node* lchlid;
    struct Node* rchlid;
}Node, * pNode;
//辅助队列使用（不带头结点的链表实现）
typedef struct tag
{
    pNode c;  //辅助队列中的节点（存放树节点的地址）
    struct tag* next;
}tag, * ptag;

int main()
{
    pNode pnew;  //指向新申请的树的节点
    pNode tree = NULL;  //tree为树根，代表树，树根初始化为null
    char data;  //用来接收输入的数据
    ptag phead = NULL, ptail = NULL;  //队列头尾节点
    ptag pcur = NULL, listpnew = NULL;  //listpnew指向新申请的节点，pcur指向新节点入队时候的父节点
    while (scanf("%c", &data))
    {
        if (data == '\n')
        {
            break;
        }
        pnew = (pNode)calloc(1, sizeof(Node));  //树的节点申请空间
        pnew->data = data;
        listpnew = (ptag)calloc(1, sizeof(tag));  //辅助队列申请申请空间
        listpnew->c = pnew;  //将要放入树中的节点入队
        if (NULL == tree)
        {
            tree = pnew;  //当树为空时，将树申请的节点pnew放入树中，pnew就是树中的第一个节点，树根tree指向第一个节点pnew
            phead = listpnew, ptail = listpnew;  //队列中只有一个节点时，队列的头尾节点都指向该节点
            pcur = listpnew;  //下一个节点放入树中时，父节点是队列中listpnew指向的节点
        }
        else 
        {
            ////先放入树中
            //if (NULL == pcur->c->lchlid)
            //{
            //    pcur->c->lchlid = pnew;
            //}
            //else if (NULL == pcur->c->rchlid)
            //{
            //    pcur->c->rchlid = pnew;
            //    pcur = pcur->next;
            //}
            ////再放入队列中
            //ptail->next = listpnew;
            //ptail = listpnew;

            //先放入队列
            ptail->next = listpnew;
            ptail = listpnew;
            //再放入树中
            if (NULL == pcur->c->lchlid)
            {
                pcur->c->lchlid = pnew;
            }
            else if (NULL == pcur->c->rchlid)
            {
                pcur->c->rchlid = pnew;
                pcur = pcur->next;
            }
        }
    }
    return 0;
}

二叉树前序中序后序遍历

二叉树前序中序后序遍历代码是在二叉树层次建树的基础上增加前序中序后序遍历代码实现的。 前序遍历是先打印自身，再打印左子树，再打印右子树。（这里通过PreOrder实现） ::: tip 前序遍历又叫深度优先遍历。 ::: 中序遍历是先打印左子树，再打印当前节点，再打印右子树。（这里通过InOrder实现） 后序遍历是先打印左子树，再打印右子树，再打印当前节点。（这里通过PostOrder实现） ::: warning 每棵树的打印输出节点都在这棵树的父节点旁，递归操作时每次只看一棵子树。 ::: 前序遍历代码：

void PreOder(BiTree tree)
{
    if (tree != NULL)
    {
        printf("%c", tree->data);  //打印当前节点
        PreOder(tree->lchild);  //打印左子树
        PreOder(tree->rchild);  //打印右子树
    }
}

中序遍历代码：

void InOder(BiTree tree)
{
    if (tree != NULL)
    {
        InOder(tree->lchild);  //打印左子树
        printf("%c", tree->data);  //打印当前节点
        InOder(tree->rchild);  //打印右子树
    }
}

后序遍历代码：

void PostOder(BiTree tree)
{
    if (tree != NULL)
    {
        PostOder(tree->lchild);  //打印左子树
        PostOder(tree->rchild);  //打印右子树
        printf("%c", tree->data);  //打印当前节点
    }
}

二叉树层序遍历

::: tip 层序遍历又称广度优先遍历。 ::: 层序遍历类似于层次建树原理，需要使用辅助队列。层序遍历是在之前代码中前中后序遍历时已经建好的树的基础上再建一个辅助队列完成。 ::: tip 原理：先将元素a入队，然后判断队列是否为空，如果队列不为空，将a出队（并打印），出队后将a销毁，再判断最左孩子是否为空，如不为空则入队（b），再判断右孩子是否为空，如不为空则入队（c），重新进行循环判断是否为空（队列中有b、c），进入循环，打印并出队b… ::: 层序遍历代码：

//层序遍历（广度优先遍历）
void LevelOrder(BiTree tree)
{
    LinkQueue Q;
    InitQueue(Q);
    BiTree p;  //存储出队节点
    EnQueue(Q,tree);  //根节点入队
    while(!IsEmpty(Q))  //队列不为空则进入循环
    {
        DeQueue(Q,p);
        putchar(p->data);
        if(NULL!=p->lchild)  //可以简写成p->lchild
        {
            EnQueue(Q,p->lchild);
        }
        if(NULL!=p->rchild)
        {
            EnQueue(Q,p->rchild);
        }
    }
}

二叉树的前中后序和层序遍历全部代码： function.h：

#include <stdio.h>
#include <stdlib.h>

typedef char BiElemType;
//树的队列
typedef struct BiTNode
{
    BiElemType data;
    struct BiTNode* lchild;
    struct BiTNode* rchild;
}BiTNode, * BiTree;

//建树辅助队列使用，队列是链表实现的
typedef struct tag
{
    BiTree p;  //树的某一结点的地址，需要使用指针
    struct tag* pnext;  //链表中的next指针，用于指向下一个节点
}tag_t, * ptag_t;

//层序遍历辅助队列使用
typedef BiTree Elemtype;
typedef struct LinkNode  //链表
{
    Elemtype data;  //层序遍历中存放的是树的节点指针（BiTree类型）
    struct LinkNode* next;
}LinkNode;
typedef struct  //队列
{
    LinkNode* front, * rear;
}LinkQueue;

//函数调用
void InitQueue(LinkQueue& Q);
bool IsEmpty(LinkQueue Q);
void EnQueue(LinkQueue& Q, Elemtype x);
bool DeQueue(LinkQueue& Q, Elemtype& x);

queue.cpp：

#include "function.h"

//队列初始化，带头节点的链表实现
void InitQueue(LinkQueue& Q)
{
    Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));  //头节点
    Q.front->next = NULL;
}

//判断队列是否为空
bool IsEmpty(LinkQueue Q)
{
    return Q.front == Q.rear;  //判断为真（相等）返回1（true）
}

//入队
void EnQueue(LinkQueue& Q, Elemtype x)
{
    LinkNode* pnew = (LinkNode*)malloc(sizeof(LinkNode));
    pnew->data = x;
    pnew->next = NULL;
    Q.rear->next = pnew;  //原队尾rear的next指向NULL，pnew从队尾插入，rear的next指向新队尾
    Q.rear = pnew;  //rear指向新的队尾
}

//出队
bool DeQueue(LinkQueue& Q, Elemtype& x)
{
    if (Q.front == Q.rear)
    {
        return false;
    }
    //x = Q.front->data;
    LinkNode* p = Q.front->next;
    x = p->data;
    Q.front->next = p->next;
    if (p == Q.rear)  //该节点为链表中最后一个节点
    {
        Q.rear = Q.front;  //rear指向front指向位置
    }
    free(p);
    p = NULL;
    return true;
}

main.cpp：

#include "function.h"

//前序遍历（深度优先遍历）
void PreOrder(BiTree tree)
{
    if (tree != NULL)
    {
        printf("%c", tree->data);  //打印当前节点
        PreOrder(tree->lchild);  //打印左子树
        PreOrder(tree->rchild);  //打印右子树
    }
}

//中序遍历
void InOrder(BiTree tree)
{
    if (tree != NULL)
    {
        InOrder(tree->lchild);  //打印左子树
        printf("%c", tree->data);  //打印当前节点
        InOrder(tree->rchild);  //打印右子树
    }
}

//后序遍历
void PostOrder(BiTree tree)
{
    if (tree != NULL)
    {
        PostOrder(tree->lchild);  //打印左子树
        PostOrder(tree->rchild);  //打印右子树
        printf("%c", tree->data);  //打印当前节点
    }
}

//层序遍历（广度优先遍历）
void LevelOrder(BiTree tree)
{
    LinkQueue Q;
    InitQueue(Q);
    BiTree p;  //存储出队节点
    EnQueue(Q, tree);  //根节点入队
    while (!IsEmpty(Q))  //队列不为空则进入循环
    {
        DeQueue(Q, p);
        putchar(p->data);
        if (NULL != p->lchild)
        {
            EnQueue(Q, p->lchild);
        }
        if (NULL != p->rchild)
        {
            EnQueue(Q, p->rchild);
        }

    }
}

int main()
{
    //层次建树
    BiTree pnew;  //pnew指向树申请的新节点的指针
    BiTree tree = NULL;  //tree指向树根（第一个节点，即根节点），用来代表树，树根需要初始化为NULL
    char data;  //要输入的元素（abcdefghij）
    ptag_t phead = NULL, ptail = NULL;  //队列头指针和队列尾指针初始化为NULL
    ptag_t list_pnew = NULL, pcur = NULL;  //辅助队列中list_pnew和树中pnew对应，pcur指向当前读进树中的节点的父亲节点
    while (scanf("%c", &data))  //把每一个字符作为树的节点存入树中
    {
        if (data == '\n')
        {
            break;  //读取输入内容时，末尾的\n不放入树
        }
        pnew = (BiTree)calloc(1, sizeof(BiTNode));  //每读入一个数据，都要开辟节点
        //使用malloc开辟节点时，读取的字符存在data中，但是左右孩子需要初始化为NULL，比较麻烦
        //calloc申请空间的大小是两个参数的乘积，calloc申请空间后会先将空间初始化为0
        pnew->data = data;  //将读进来的数据存进申请树的结构体的data中
        list_pnew = (ptag_t)calloc(1, sizeof(tag_t));  //该节点的地址放入辅助队列，给队列节点申请空间
        list_pnew->p = pnew;  //队列结构体中p存放的是树中对应结点pnew的地址
        //判断是否为树的第一个节点
        if (NULL == tree)  //当tree=NULL时，树为空，即此时树中开辟的节点是根节点，辅助队列中申请的是第一个节点
        {
            tree = pnew;  //树为空时，tree指向读入的第一个节点（根节点），其余字符读进来时tree不为空
            phead = ptail = list_pnew;  //起始时辅助队列中队列头和队列尾都指向第一个节点a
            pcur = list_pnew;  //pcur指向读入节点的父亲节点，只有一个根节点a时，pcur指向根节点a
        }
        else {
            //元素b先入队列
            ptail->pnext = list_pnew;  //读入新元素（b）的地址放在队列尾指针的pnext域
            ptail = list_pnew;  //新读入的元素b变为队列新的尾部，
            //节点b放入树中
            if (NULL == pcur->p->lchild)
            {
                pcur->p->lchild = pnew;  //当pcur指向的节点a的左孩子为NULL时，a的左孩子指向新节点b
            }
            else if (NULL == pcur->p->rchild)  //读入第三个元素c时
            {
                pcur->p->rchild = pnew;  //当pcur指向的节点a的左孩子不为NULL右孩子为NULL时，a的又孩子指向新节点c
                pcur = pcur->pnext;  //pcur->p即节点a的左右孩子都已经放了节点后，当前节点放满，pcur指向下一个节点b
            }
        }
    }
    printf("------------------前序遍历------------------\n");
    PreOrder(tree);
    printf("\n");
    printf("------------------中序遍历------------------\n");
    InOrder(tree);
    printf("\n");
    printf("------------------后序遍历------------------\n");
    PostOrder(tree);
    printf("\n");
    printf("------------------层序遍历------------------\n");
    LevelOrder(tree);
    printf("\n");
    return 0;
}

二叉树的前中后序和层序遍历全部代码：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

typedef char Elemtype;
//建树使用
typedef struct Node
{
    Elemtype data;
    struct Node* lchlid;
    struct Node* rchlid;
}Node, * pNode;
//辅助队列使用（不带头结点的链表实现）
typedef struct tag
{
    pNode c;  //辅助队列中的节点（存放树节点的地址）
    struct tag* next;
}tag, * ptag;
//层序遍历使用
typedef struct LinkNode  //节点的结构体
{
    pNode data;
    struct LinkNode* next;
}LinkNode;
typedef struct  //队列的结构体
{
    LinkNode* front, * rear;
}LinkQueue;

//前序遍历（深度优先遍历）
void PreOrder(pNode tree)
{
    if (NULL != tree)
    {
        printf("%c", tree->data);
        PreOrder(tree->lchlid);
        PreOrder(tree->rchlid);
    }
}
//中序遍历
void InOrder(pNode tree)
{
    if (NULL != tree)
    {
        InOrder(tree->lchlid);
        printf("%c", tree->data);
        InOrder(tree->rchlid);
    }
}
//后序遍历
void PostOrder(pNode tree)
{
    if (NULL != tree)
    {
        PostOrder(tree->lchlid);
        PostOrder(tree->rchlid);
        printf("%c", tree->data);
    }
}
//层序遍历
//带头结点的队列
void InitQueue(LinkQueue& Q)  //初始化
{
    Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
}
bool IsEmpty(LinkQueue Q)//判断是否为空
{
    return Q.front == Q.rear;
}
void EnQueue(LinkQueue& Q,pNode x)//入队
{
    LinkNode* pnew = (LinkNode*)malloc(sizeof(LinkNode));
    pnew->data = x;
    Q.rear->next = pnew;
    Q.rear = pnew;
}
bool DeQueue(LinkQueue& Q, pNode& x)//出队
{
    if (Q.front==Q.rear)
    {
        return false;
    }
    LinkNode* p = Q.front->next; //带头结点的队列，先进先出，队头出队，队尾入队
    x = p->data;
    Q.front->next = p->next;
    if (p == Q.rear)
    {
        Q.rear = Q.front;  //链表只剩余一个节点被删除后，rear要指向front，否则队列判断为空时会出错
    }
    free(p);
    p = NULL;
    return true;
}
void LevelOrder(pNode tree)
{
    LinkQueue Q;
    InitQueue(Q);
    EnQueue(Q,tree);
    pNode p;  //用来存储出队节点
    while (!IsEmpty(Q))
    {
        DeQueue(Q, p);
        putchar(p->data);
        if (NULL != p->lchlid)
        {
            EnQueue(Q, p->lchlid);
        }
        if (NULL != p->rchlid)
        {
            EnQueue(Q, p->rchlid);
        }
    }
}
int main()
{
    pNode pnew;  //指向新申请的树的节点
    pNode tree = NULL;  //tree为树根，代表树，树根初始化为null
    char data;  //用来接收输入的数据
    ptag phead = NULL, ptail = NULL;  //队列头尾节点
    ptag pcur = NULL, listpnew = NULL;  //listpnew指向新申请的节点，pcur指向新节点入队时候的父节点
    while (scanf("%c", &data))
    {
        if (data == '\n')
        {
            break;
        }
        pnew = (pNode)calloc(1, sizeof(Node));  //树的节点申请空间
        pnew->data = data;
        listpnew = (ptag)calloc(1, sizeof(tag));  //辅助队列申请申请空间
        listpnew->c = pnew;  //将要放入树中的节点入队
        if (NULL == tree)
        {
            tree = pnew;  //当树为空时，将树申请的节点pnew放入树中，pnew就是树中的第一个节点，树根tree指向第一个节点pnew
            phead = listpnew, ptail = listpnew;  //队列中只有一个节点时，队列的头尾节点都指向该节点
            pcur = listpnew;  //下一个节点放入树中时，父节点是队列中listpnew指向的节点
        }
        else 
        {
            ////先放入树中
            //if (NULL == pcur->c->lchlid)
            //{
            //    pcur->c->lchlid = pnew;
            //}
            //else if (NULL == pcur->c->rchlid)
            //{
            //    pcur->c->rchlid = pnew;
            //    pcur = pcur->next;
            //}
            ////再放入队列中
            //ptail->next = listpnew;
            //ptail = listpnew;

            //先放入队列
            ptail->next = listpnew;
            ptail = listpnew;
            //再放入树中
            if (NULL == pcur->c->lchlid)
            {
                pcur->c->lchlid = pnew;
            }
            else if (NULL == pcur->c->rchlid)
            {
                pcur->c->rchlid = pnew;
                pcur = pcur->next;
            }
        }
    }
    PreOrder(tree);
    InOrder(tree);
    printf("\n");
    PostOrder(tree);
    printf("\n");
    LevelOrder(tree);
    return 0;
}

树与二叉树 WPL：树的所有叶结点的带权路径长度之和，称为树的带权路径长度表示为WPL。（WPL只涉及叶子节点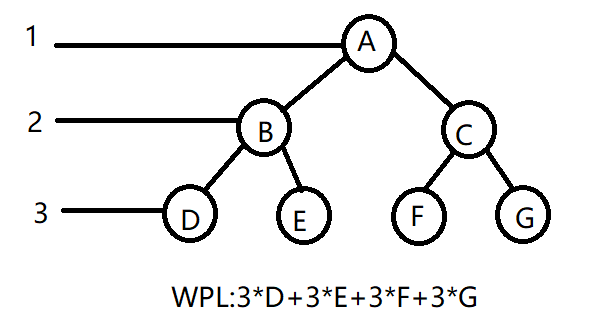）如上图，每个叶节点的权值为节点的data值，深度为层的深度。 ::: tip C++的static变量是静态局部变量。static变量在函数内定义, 生存期为整个源程序，但作用域与局部变量相同，只能在定义该变量的函数内使用。退出该函数后，尽管该变量还继续存在，但不能使用它。递归的过程中只生效一次。 :::

代码实现： function.h：

#pragma once
#include <stdio.h>
#include <stdlib.h>
typedef int BiElemType;
typedef struct BiTNode
{
    BiElemType weight;
    struct BiTNode* left;
    struct BiTNode* right;
}BiTNode, * BiTree;

//建树辅助队列使用，队列是链表实现的
typedef struct tag
{
    BiTree p;  //树的某一结点的地址，需要使用指针
    struct tag* pnext;  //链表中的next指针，用于指向下一个节点
}tag_t, * ptag_t;

//层序遍历辅助队列使用
typedef BiTree Elemtype;
typedef struct LinkNode  //链表
{
    Elemtype data;  //层序遍历中存放的是树的节点指针（BiTree类型）
    struct LinkNode* next;
}LinkNode;
typedef struct  //队列
{
    LinkNode* front, * rear;
}LinkQueue;

//函数调用
void InitQueue(LinkQueue& Q);
bool IsEmpty(LinkQueue Q);
void EnQueue(LinkQueue& Q, Elemtype x);
bool DeQueue(LinkQueue& Q, Elemtype& x);

main.cpp：

#define _CRT_SECURE_NO_WARNINGS
#include "function.h"

////使用全局变量时
//int wpl = 0;  //全局变量
////前序遍历
//void WPL_PreOrder(BiTree tree, int deep)
//{
//    if (NULL != tree)
//    {
//        /*printf("Elem%c---%d", tree->weight, deep);*/
//        if (tree->left == NULL && tree->right == NULL)  //判断是否是叶子节点，不是叶子节点才需要向下递归
//        {
//            wpl = wpl + tree->weight * deep;
//        }
//        WPL_PreOrder(tree->left, deep + 1);  //每次向下遍历，深度（层数+1）
//        WPL_PreOrder(tree->right, deep + 1);
//    }
//}

//使用局部静态变量时
//前序遍历
int WPL_PreOrder(BiTree tree, int deep)
{
    static int wpl;
    if (NULL != tree)
    {
        /*printf("Elem%c---%d", tree->weight, deep);*/
        if (tree->left == NULL && tree->right == NULL)  //判断是否是叶子节点，不是叶子节点才需要向下递归
        {
            wpl = wpl + tree->weight * deep;
        }
        WPL_PreOrder(tree->left, deep + 1);  //每次向下遍历，深度（层数+1）
        WPL_PreOrder(tree->right, deep + 1);
    }
    return wpl;
}

int main()
{
    //层次建树
    BiTree pnew;  //pnew指向树申请的新节点的指针
    BiTree tree = NULL;  //tree指向树根（第一个节点，即根节点），用来代表树，树根需要初始化为NULL
    char data;  //要输入的元素（abcdefghij）
    ptag_t phead = NULL, ptail = NULL;  //队列头指针和队列尾指针初始化为NULL
    ptag_t list_pnew = NULL, pcur = NULL;  //辅助队列中list_pnew和树中pnew对应，pcur指向当前读进树中的节点的父亲节点
    while (scanf("%c", &data))  //把每一个字符作为树的节点存入树中
    {
        if (data == '\n')
        {
            break;  //读取输入内容时，末尾的\n不放入树
        }
        pnew = (BiTree)calloc(1, sizeof(BiTNode));  //每读入一个数据，都要开辟节点
        //使用malloc开辟节点时，读取的字符存在data中，但是左右孩子需要初始化为NULL，比较麻烦
        //calloc申请空间的大小是两个参数的乘积，calloc申请空间后会先将空间初始化为0
        pnew->weight = data;  //将读进来的数据存进申请树的结构体的data中
        list_pnew = (ptag_t)calloc(1, sizeof(tag_t));  //该节点的地址放入辅助队列，给队列节点申请空间
        list_pnew->p = pnew;  //队列结构体中p存放的是树中对应结点pnew的地址
        //判断是否为树的第一个节点
        if (NULL == tree)  //当tree=NULL时，树为空，即此时树中开辟的节点是根节点，辅助队列中申请的是第一个节点
        {
            tree = pnew;  //树为空时，tree指向读入的第一个节点（根节点），其余字符读进来时tree不为空
            phead = ptail = list_pnew;  //起始时辅助队列中队列头和队列尾都指向第一个节点a
            pcur = list_pnew;  //pcur指向读入节点的父亲节点，只有一个根节点a时，pcur指向根节点a
        }
        else {
            //元素b先入队列
            ptail->pnext = list_pnew;  //读入新元素（b）的地址放在队列尾指针的pnext域
            ptail = list_pnew;  //新读入的元素b变为队列新的尾部，
            //节点b放入树中
            if (NULL == pcur->p->left)
            {
                pcur->p->left = pnew;  //当pcur指向的节点a的左孩子为NULL时，a的左孩子指向新节点b
            }
            else if (NULL == pcur->p->right)  //读入第三个元素c时
            {
                pcur->p->right = pnew;  //当pcur指向的节点a的左孩子不为NULL右孩子为NULL时，a的又孩子指向新节点c
                pcur = pcur->pnext;  //pcur->p即节点a的左右孩子都已经放了节点后，当前节点放满，pcur指向下一个节点b
            }
        }
    }
    printf("------------------前序遍历------------------\n");
    //WPL_PreOrder(tree,0);  //wpl统计的是路径，首次传入值应该为0。全局变量使用
    printf("\n");
    //printf("wpl=%d", wpl);  //全局变量使用
    printf("wpl=%d", WPL_PreOrder(tree, 0));  //局部静态变量使用
    return 0;
}

二叉树层次建树

二叉树前序中序后序遍历

二叉树层序遍历

Android进阶之旅-(NDK实战篇之数据结构算法进阶)

Andriod第三方源码分析

热门文章