计算机中存储有符号数的时候是按照补码的形式存进去的。 原码是数字的二进制表示，补码是原码取反+1。 正数的原反补相同。 原码：最高位表示符号位，其余位表示数值位的编码称为原码。正数的符号位为0，负数的符号位为1。 负数的反码：原码的符号位保持不变，数值位逐位取反，可得原码的反码。 负数的补码：在反码的基础上加1，可得原码的补码。 1) 负数原码转换为反码：符号位不变，数值位分别“按位取反”。 2) 负数反码转换为原码：符号位不变，数值位分别“按位取反”。 3) 负数原码转换为补码：符号位不变，数值位按位取反，末位再加1。 4) 负数补码转换为原码：符号位不变，末位-1，数值位按位取反（逆运算）。 ::: warning 补码的补码是原码，补码转换原码：符号位不变，数值位按位取反，末位再加1。 补码的最高位一定是1。 :::
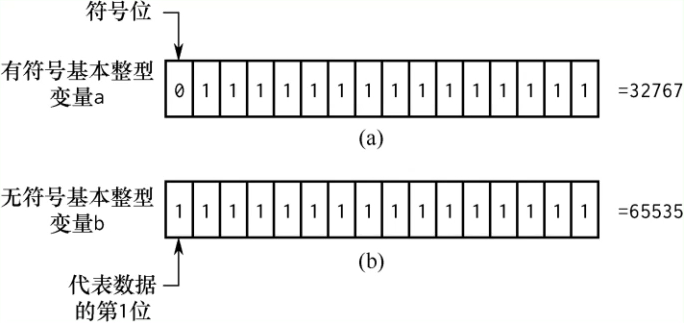
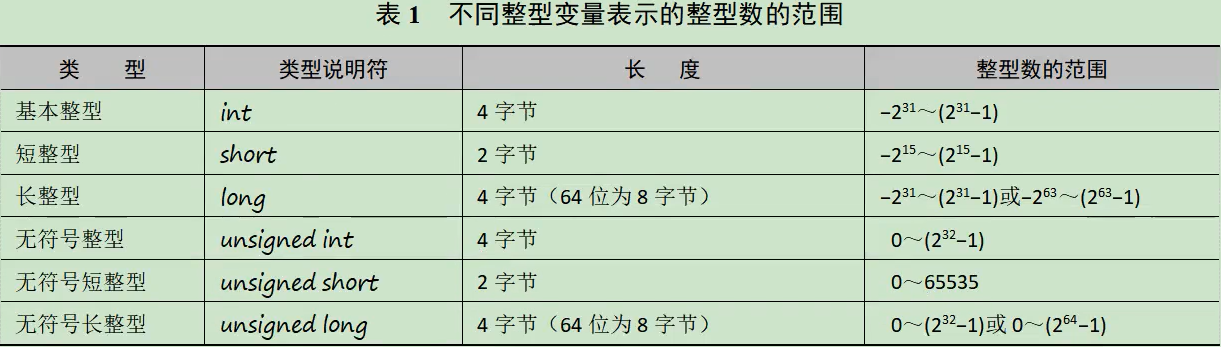
整型不同类型
下图是整型变量的六种类型：
上图括号中的内容可省略。默认是有符号类型，signed是缺省的。
下图是有符号short类型和无符号short类型二进制数首位的对比：
计算机输入一个short类型的有符号数：
补码： 1000 0000 0000 0000 计算机读入首位为1，记负号
取反： 111 1111 1111 1111 对数值位取反
数值位+1：1000 0000 0000 0000 +1得到32768，加上符号位是-32768
（二进制数不满16位在高位补0）
溢出
有符号的short类型的最大值是32767（0111 1111 1111 1111），如果对它+1，变为1000 0000 0000 0000，即-32768，发生溢出。 解决溢出的方法是使用更大的空间存储，如int类型。
有符号的short类型的变量b和无符号short类型的变量n，同时赋值为0x8056，b输出-32682，n输出32854。 原因如下： 0x8056转换为二进制为：1000 0000 0101 0110。 b是有符号数，先输出负号，取反得000 0000 0101 0110，+1得(0)000 0000 0101 0111，即32682，加上负号为b=-32682。 n是无符号数，1000 0000 0101 0110，即n=32854。
::: warning 无符号数的所有位数都用来表示数字大小，没有原反补码，只有有符号数才有原反补码。 C语言规定无符号类型整型输出应使用%u，有符号类型整型输出应使用%d。 :::
浮点数IEEE754标准
C语言使用float和double关键字定义浮点型变量。
无论是32位系统还是64位系统，float类型都占用4字节，double类型都占用8字节。
浮点型数据的组成如下：
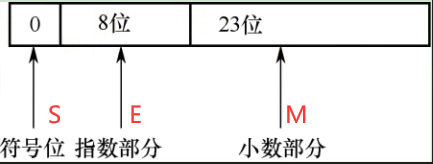浮点型数据按照指数形式存储。
系统把浮点型数据分成小数部分（M）和指数部分（E）并分别存放。
指数有符号位（S）。符号位（数符）为0表示正数，为1表示负数。
小数部分表示数值，使用小数部分×指数部分。
指数部分存放的值是2的?次幂。
计算40 90 00 00的浮点数的值：
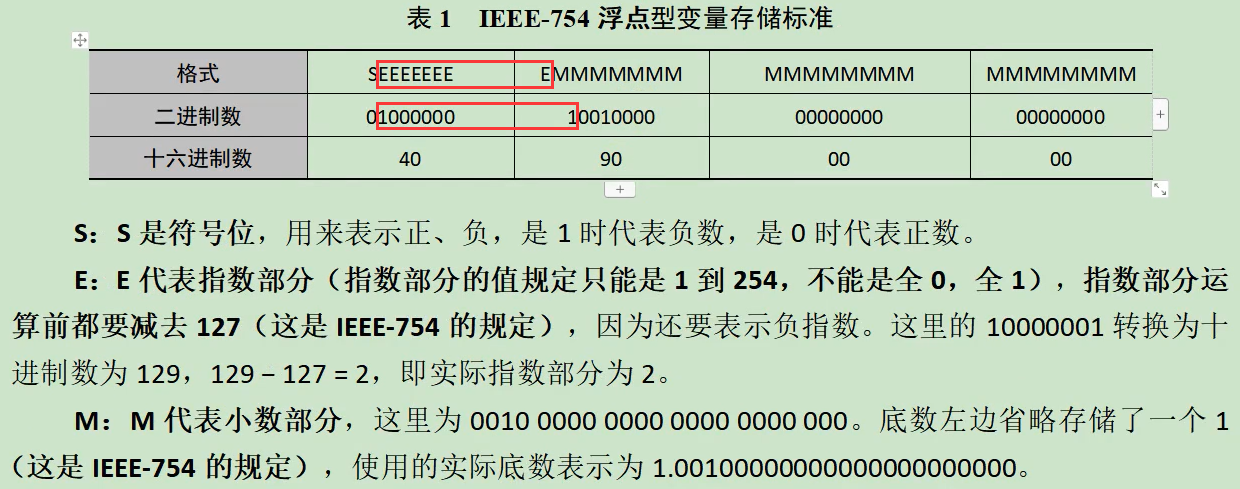上图实际指数部分的2表示2的2次幂，为4。
小数部分实际底数为1.001，是二进制数，1为2的0次幂，0为2的-1、-2次幂，1为2的-3次幂，化为十进制相加得1+0.125=1.125。
小数部分和指数部分相乘得到1.125*4=4.5。
十六进制数为40 90 00 00，内存中小端存储为00 00 90 40。
上述计算也可以将1.001的二进制数左移两位（左移一位相当于×2），变为100.1，2的2次幂+2的-1次幂=4.5。
上述表格可以变为如下：
计算35 5e ba 3f的值：
内存中是35 5e ba 3f，内存中是小端存储，所以实际值应为0x3ba5e35，转换成二进制为011 1111 1011 1010 0101 1110 0011 0101。
底数左边忽略了一个1，所以实际底数应该是1.011 1111 1011 1010 0101 1110 0011 0101。
指数部分0111 1111，十进制为127，根据IEEE-754的规定-127后为0，实际指数为0，2的0次幂为1，1.011 1111 1011 1010 0101 1110 0011 0101无需改变，直接换为十进制为2的0次幂+2的-2次幂+2的-3次幂…
受限于小数部分长度，浮点数小数部分可以近似得到一个浮点数，如下：
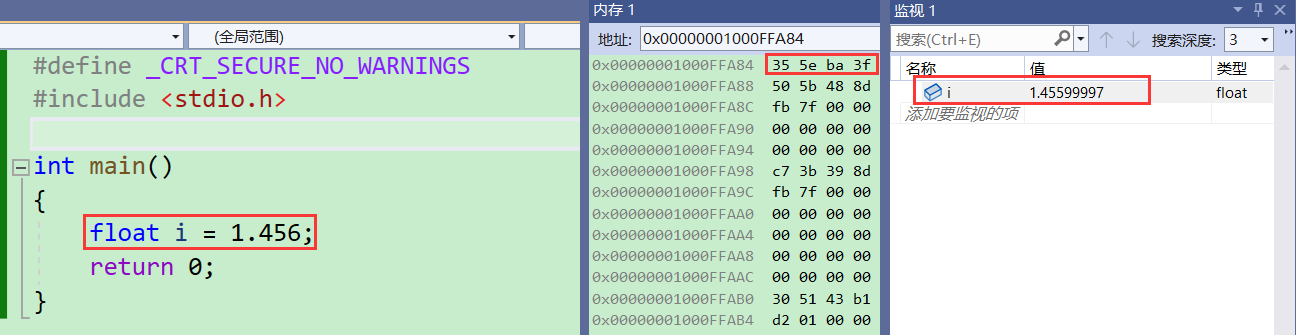指数部分为1，小数部分不需左移（×2）。
浮点数精度丢失
有效数字从左边第一个不为0的数字算起，到最后一个不为0的数字结束，称为精度。
如float类型的变量1.23456789e10，e10表示10的10次方，有效数字为12345678900，有效数字11位，超过float类型的有效数字7位，就会发生精度丢失。解决方法是将类型变为double。
::: warning
float和double都可以使用%f输出，double常用%lf。scanf读取double时只能使用%lf，否则读取不到。
:::
整型数可以放进浮点数变量中，double也可以存储整型。 int是10位有效数字，int发生溢出时，转成float会发生溢出，转成double不会丢失精度。
