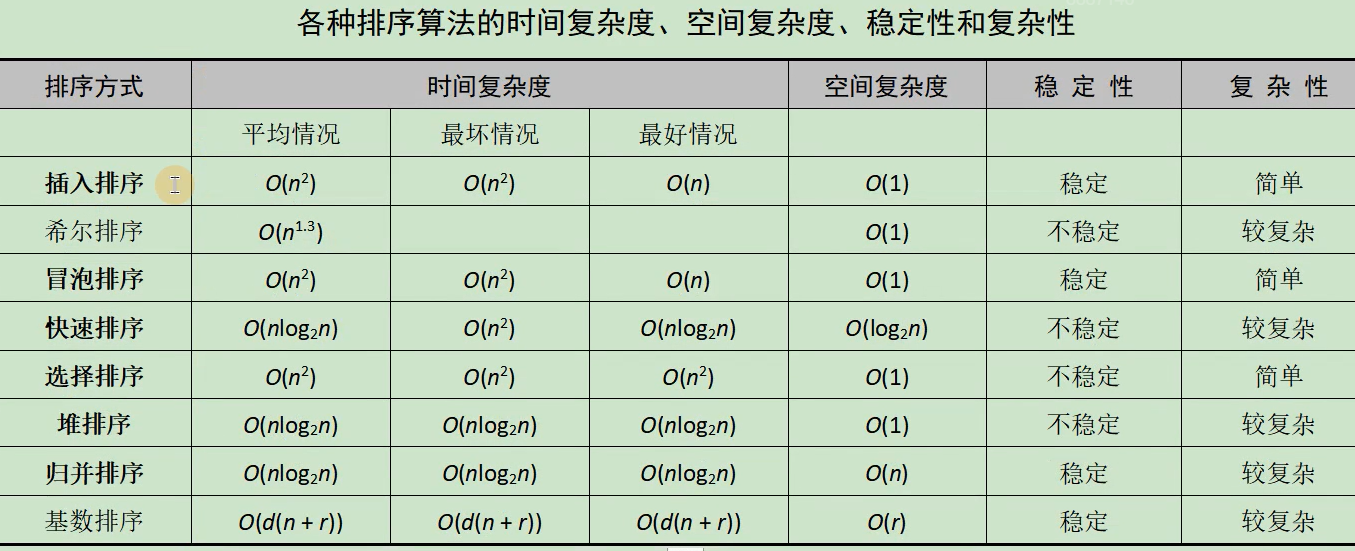
排序算法（冒泡、快速、插入）

排序算法（冒泡、快速、插入） 稳定性：排序前后相等的元素位置是否会被交换。

冒泡排序

排序算法（冒泡、快速、插入） strcpy只能拷贝字符串，整型或浮点型数组需要用memcpy。 memcpy称为内存拷贝接口，可以将某一段连续的内存放入另一段连续的内存中。 在使用随机数的代码中使用固定的数组有利于调试。 ::: tip memcpy函数声明： void * memcpy ( void * destination, const void * source, size_t num ); destination：指向用于存储复制内容的目标数组，类型强制转换为 void * 指针。 source：指向要复制的数据源，类型强制转换为 void * 指针。 num：要被复制的字节数（数组大小）。 :::

排序往往是通过两层循环实现的，如下：排序算法（冒泡、快速、插入） 冒泡排序属于交换类排序，内层循环控制相邻元素的比较和交换；外层循环将所有未确定位置的元素依次交给内层循环。 内层循环比较清晰，外层循环不明确时候，先构建两层循环框架，优先写内层循环， 如下：

for(i;;)
{
        for(j=len-1;j>0;j--)//内层循环，控制相邻元素的比较和交换
        {
                if(arr[j]<arr[j-1])//由此处可得，要保证arr[j-1]能去到数组内值，j的范围应是j>0
                ……
        }
}

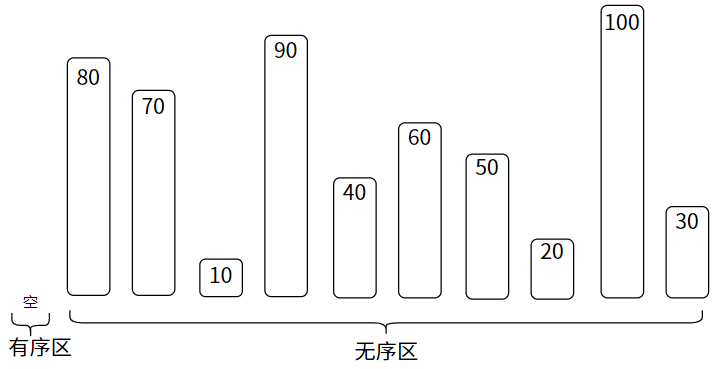
由上图，一次内层循环只能找到数组中最小数字的位置，下一次内层循环找到数组中第二小的数字位置，依次向下，每次循环时，内层循环的范围都要-1，原因是每次进行内层循环时，都会找到一个当前最小的数字并放在当前数组中剩余数字的最前面位置。即每进行一次内层循环后，j的条件都会发生改变，第一次j>0，第二次j>1…此时控制外层循环的变量i从0开始，每次执行++操作，和内层循环的条件改变所吻合，即可以将内层循环的控制条件改为j>i。 当外层循环进入到末尾时，最后两个元素的比较时，如下图的arr[6]和arr[7]，此时j=7，i=6，只需要通过内层循环就可以完成排序。 排序算法（冒泡、快速、插入）

冒泡排序代码：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>  //memcpy使用

typedef int Elemtype;
typedef struct
{
    Elemtype* arr;
    int lenth;
}SSTable;

//初始化
void Init_ST(SSTable& ST, Elemtype len)
{
    ST.lenth = len;
    ST.arr = (Elemtype*)malloc(sizeof(Elemtype) * ST.lenth);
    int i;
    srand(time(NULL));
    for (i = 0; i < ST.lenth; i++)  //没有哨兵
    {
        ST.arr[i] = rand() % 100;
    }
}

//打印顺序表
void ST_Print(SSTable ST)
{
    int i;
    for (i = 1; i < ST.lenth; i++)
    {
        printf("%3d", ST.arr[i]);
    }
    printf("\n");
}

//冒泡排序
void bubble_sort(Elemtype* arr, Elemtype len)  //数组ST.arr的类型是Elemtype*
{

}
int main()
{
    SSTable ST;
    //在使用随机数的代码中使用固定的数组有利于调试
    //Elemtype A[10] = { 64,94,95,79,69,84,18,22,12,78 };
    //memcpy(ST.arr, A, sizeof(A));
    Init_ST(ST, 10);
    ST_Print(ST);
    bubble_sort(ST.arr, 10);  //将数组ST.arr传入（也可以传ST）
    return 0;
}

计算时间复杂度与空间复杂度

时间复杂度是程序实际的运行次数，内层是j>i，外层i的值是从0到N-1，i每次+1，所以程序的总运行次数是1+2＋3+…+(N -1)，即从1一直加到N-1，这是等差数列求和，得到的结果是N(N -1)/2，即总计运行了这么多次，忽略低阶项和高阶项的首项系数，因为时间复杂度为O(n²)。 当输入元素N改变时，没有引入新的变量，因为未使用额外的空间（额外空间必须与输入元素的个数N相关)，所以空间复杂为O(1)。 如果数组本身有序，那么就是最好的时间复杂度O(n)。 排序算法的时间复杂度分为最坏、平均、最好。 冒泡排序的最坏和平均时间复杂度都是O(n²)，最好是O(n)。

快速排序

排序算法（冒泡、快速、插入） 挖坑法实现分割函数原理： 1.将数组中最左边的元素值确定为分割值并存储。 2.建立while循环将数组从右往左分别和分割值进行比较，小于分割值的元素将覆盖在分割元素的位置（快排后小于分割值的元素都会出现在分割元素左边），此时low向后移动一个元素，即low++，大于分割值的元素位置不变，high向前移动一个元素，即high--，直到最后分割值左右各有一个元素，此时不需快排，即外层循环的条件是low<high。还需要有一个内层的循环，分别找到大于分割值的元素和小于分割值的元素。快速排序代码：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <time.h>  //随机数使用
#include <stdlib.h>  //随机数使用
#include <string.h>  //memcpy使用

typedef int Elemtype;
typedef struct
{
    Elemtype arr[10];
    int len;
}SSTable;

void InitTable(SSTable& ST, Elemtype x)
{
    int i;
    ST.len = x;
    srand(time(NULL));
    for (i = 0; i < ST.len; i++)
    {
        ST.arr[i] = rand() % 100;
    }
}

void Print(SSTable ST)
{
    int i;
    for (i = 0; i < ST.len; i++)
    {
        printf("%3d", ST.arr[i]);
    }
    printf("\n");
}

//分割函数(快速排序的核心)
int partition(Elemtype arr[], int low, int high)
//经过一次分割后，分割元素到达数组中间，小于分割元素的在分割元素左边，大于分割元素的在分割元素右边
{
    Elemtype pivot = arr[low];  //将数组最左边的元素值当作分割值并存储
    while (low < high)
    {
        //循环条件中的=可以解决生成随机数中含有相等数值的程序卡死问题
        while (low < high && arr[high] >= pivot)  //数组从后向前遍历，找到比分割值小的元素
        {
            high--;  //使high指向该元素
        }
        arr[low] = arr[high];  //比分割值小的元素覆盖掉low指向的元素（low原本指向的元素已经当作分割值存储在pivot中）
        while (low < high && arr[low] <= pivot)  //数组从前向后遍历，找到比分割值大的元素
        {
            low++;  //使low指向该元素
        }
        arr[high] = arr[low];  //比分割值大的元素覆盖掉high指向的元素（此时high原本指向的元素已经放在low指向的前一个元素）
    }
    arr[low] = pivot;  //将分割值放在数组元素中间位置（low=high）
    return low;  //将分割值的元素数组下标返回到QucikSort函数中
}

void QucikSort(Elemtype arr[], int low, int high)  //low表示数组最左边的元素，high表示数组最右边的元素
{
    if (low < high)  //当分割元素左右两边的数组中各只剩下一个元素时，即low=high时，无需再进行排序
    {
        int pivot_pos = partition(arr, low, high);  //存储分割元素的位置（分割元素的下标）
        QucikSort(arr, low, pivot_pos - 1);  //对分割元素之前的数组进行快速排序
        QucikSort(arr, pivot_pos + 1, high);  //对分割元素之后的数组进行快速排序
    }
}

int main()
{
    SSTable ST;
    InitTable(ST, 10);
    //代码调试时使用
    //Elemtype arr[10] = { 64,94,95,79,69,84,18,22,12,78 };
    //memcpy(ST.arr, arr, sizeof(arr));
    //分割函数较容易出错，调试时应将断点打在分割函数调用的下一句
    //调试过程中可以在内存视图中查看到16进制的数组元素
    Print(ST);
    QucikSort(ST.arr, 0, 9);
    Print(ST);
    return  0;
}

快速排序时间复杂度和空间复杂度

排序算法（冒泡、快速、插入）时间复杂度：在while循环内，low不断增加，high不断减少，直到low和high相等，此时数组遍历次数partition是n，递归时每次将数组分成两半，加起来循环次数是log2n，总的时间复杂度相乘得到O(nlog2n)。当数组本身有序时，最左边元素做分割值时，分割值左侧没有元素，low不断向右移动，high不动，时间复杂度达到最差的O(n²)。空间复杂度：快排递归次数和n的长度有关，n越长，每次将数组分成两半直到递归结束前执行的递归次数越多，递归次数是log2n，每一次递归中的low和high都需要占用空间。

插入排序

插入类排序分为直接插入排序、折半插入排序、希尔排序。

直接插入排序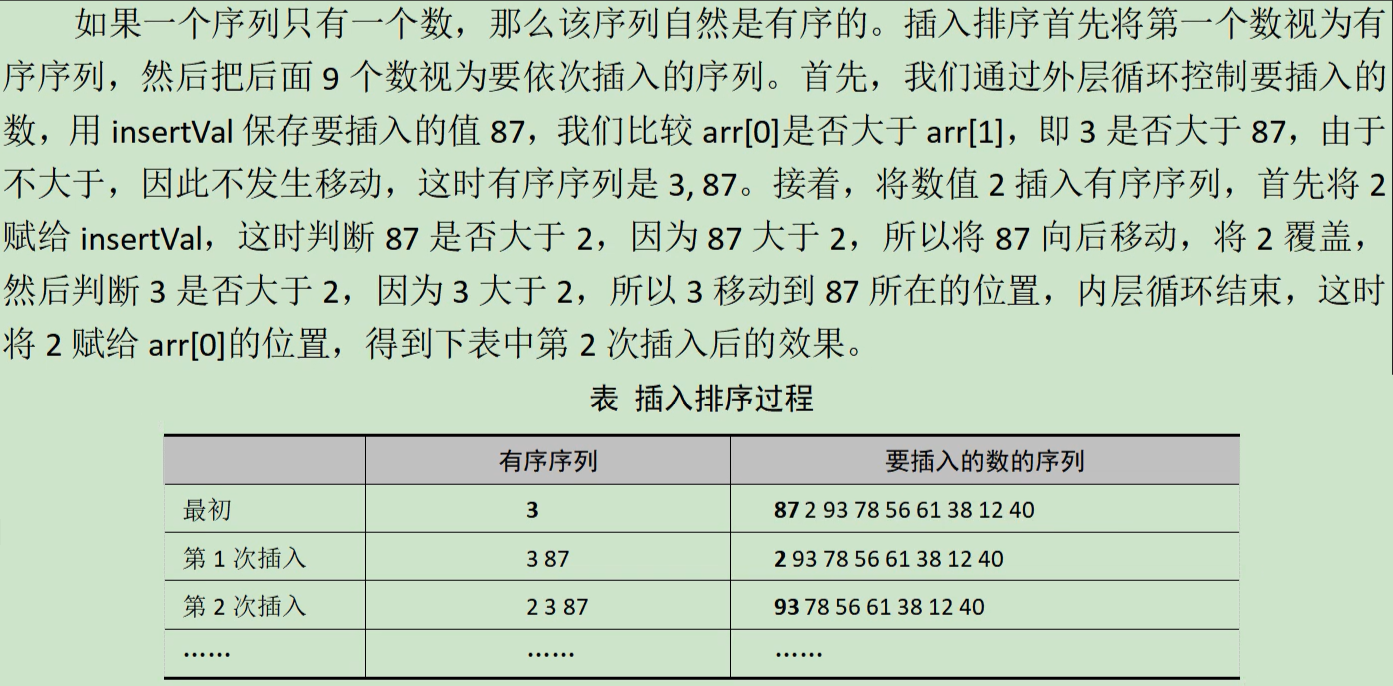：排序算法（冒泡、快速、插入）上述过程不断循环可以依次将数字插入有序序列。 ::: warning 插入排序主要用在部分数字有序的场景。 :::

插入函数中需要两层循环，外层循环控制要插入的数字，每次向后移动一个位置找到下一个要插入的数字，直到所有的数字都放入有序数组；内层循环控制每一个数字插入数组时候和数组中每一个数字比较大小，直到找到数字应该插入的位置。

for (i = 1; i < len; i++)  //外层循环控制要插入的数字，每次向后移动一个位置
{
    InsertVal = ST->arr[i];  //保存要插入的数字
    for (j = i - 1; j >= 0; j--)  //内层控制和有序数组中每一个数字的比较
    {
        if (ST->arr[j] > InsertVal)  //前一个位置上的数字大于要插入的数字时
        {
            ST->arr[j + 1] = ST->arr[j];  //前一个位置的数字覆盖到后一个位置
        }
    }
    ST->arr[j + 1] = InsertVal;  
}

当要插入的数字比有序数组中的数字都小时，j=-1，不满足循环条件跳出循环，将要插入的数字放在j+1的位置，即数组的0号位置。

时间复杂度和空间复杂度

随着有序序列的不断增加，插入排序比较的次数也会增加，插入排序的执行次数也是从1加到N-1，总运行次数为N(N -1)/2，时间复杂度依然为O(n²)。因为未使用额外的空间（额外空间必须与输入元素的个数N相关)，所以空间复杂为O(1)。 如果数组本身有序，那么就是最好的时间复杂度O(n)。

插入排序代码：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include<time.h>
#include <stdlib.h>

typedef int Elemtype;
typedef struct
{
    Elemtype* arr;
    //Elemtype arr[10];
    int len;
}SSTable;

void InitST(SSTable& ST, Elemtype len)
{
    int i;
    ST.len = len;
    ST.arr = (Elemtype*)malloc(sizeof(Elemtype) * ST.len);
    srand(time(NULL));
    for (i = 0; i < len; i++)
    {
        ST.arr[i] = rand() % 100;
    }
}

void Print(SSTable ST)
{
    int i;
    for (i = 0; i < ST.len; i++)
    {
        printf("%3d", ST.arr[i]);
    }
    printf("\n");
}

void InsertSort(Elemtype* arr, Elemtype len)
{
    int i, j, InsertVal;
    for (i = 1; i < len; i++)  //外层循环控制要插入的数字，每次向后移动一个位置
    {
        InsertVal = arr[i];  //保存要插入的数字
        for (j = i - 1; j >= 0 && arr[j] > InsertVal; j--)  //内层控制和有序数组中每一个数字的比较
        {
            //if (arr[j] > InsertVal)  //前一个位置上的数字大于要插入的数字时
            //{
                arr[j + 1] = arr[j];  //前一个位置的数字覆盖到后一个位置
            //}
        }
        arr[j + 1] = InsertVal;  
        //数组下标j的值赋给j+1，j的值和j+1重复，应该把要插入的数字放在j上，出循环前执行了j--，即InsertVal应赋给j+1
    }
}

int main()
{
    SSTable ST;  //申请10个元素的空间
    InitST(ST, 10);
    Print(ST);
    InsertSort(ST.arr, 10);
    Print(ST);
    return 0;
}

练习

读取10个整型数据12 63 58 95 41 35 65 0 38 44，然后通过冒泡排序，快速排序，插入排序，分别对该组数据进行排序，输出3次有序结果，每个数的输出占3个空格。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef int Elemtype;
typedef struct
{
    Elemtype* arr;
    int len;
}SSTable;

void InitST(SSTable& ST, Elemtype n)
{
    ST.len = n;
    ST.arr = (Elemtype*)malloc(sizeof(Elemtype) * ST.len);
}
void Print(SSTable ST)
{
    int i;
    for (i = 0; i < ST.len; i++)
    {
        printf("%3d", ST.arr[i]);
    }
    printf("\n");
}
void swap(int& x, int& y)
{
    int tmp;
    tmp = x;
    x = y;
    y = tmp;
}![image](https://img-hello-world.oss-cn-beijing.aliyuncs.com/imgs/4440870be5fcbc0190f31b7f7c135362.png)
void BubbleSort(SSTable& ST)
{
    int i, j;
    bool flag;
    for (i = 0; i < ST.len - 1; i++)
    {
        for (j = ST.len - 1; j > i; j--)
        {
            if (ST.arr[j] < ST.arr[j - 1])
            {
                swap(ST.arr[j], ST.arr[j - 1]);
                flag = true;
            }
        }
        if (flag == false)
        {
            return;  //内层循环依次对比相邻元素，一次都没有执行交换，说明数组有序
        }
    }
}

int partition(SSTable& ST, int low, int high)
{
    Elemtype pivot = ST.arr[low];
    while (low < high)
    {
        while (low < high && ST.arr[high] >= pivot)
        {
            high--;
        }
        ST.arr[low] = ST.arr[high];
        while (low < high && ST.arr[low] <= pivot)
        {
            low++;
        }
        ST.arr[high] = ST.arr[low];
    }
    ST.arr[low] = pivot;
    return low;
}

void QuickSort(SSTable& ST, int low, int high)
{
    if (low < high)
    {
        int pivot_pos = partition(ST, low, high);
        QuickSort(ST, low, pivot_pos - 1);
        QuickSort(ST, pivot_pos + 1, high);
    }
}

void InsertST(SSTable& ST)
{
    int i, j;
    for (i = 1; i < ST.len; i++)
    {
        Elemtype InsertVal = ST.arr[i];
        for (j = i - 1; j >= 0 && ST.arr[j] > InsertVal; j--)
        {
            ST.arr[j + 1] = ST.arr[j];
        }
        ST.arr[j + 1] = InsertVal;
    }
}

int main()
{
    SSTable ST;
    InitST(ST, 10);
    int i;
    Elemtype A[10];
    for (i = 0; i < 10; i++)
    {
        scanf("%d", &A[i]);
    }
    memcpy(ST.arr, A, sizeof(A));
    BubbleSort(ST);
    Print(ST);
    memcpy(ST.arr, A, sizeof(A));
    QuickSort(ST, 0, 9);
    Print(ST);
    memcpy(ST.arr, A, sizeof(A));
    InsertST(ST);
    Print(ST);
    return 0;
}![image](https://img-hello-world.oss-cn-beijing.aliyuncs.com/imgs/9dea314348696b6b60e3c42884d89f03.png)

12 63 58 95 41 35 65  0 38 44
  0 12 35 38 41 44 58 63 65 95
  0 12 35 38 41 44 58 63 65 95
  0 12 35 38 41 44 58 63 65 95

冒泡排序

计算时间复杂度与空间复杂度

快速排序

快速排序时间复杂度和空间复杂度

插入排序

时间复杂度和空间复杂度

练习

Java可重入锁原理与源码分析

Android进阶之旅-(NDK实战篇之数据结构算法进阶)

热门文章