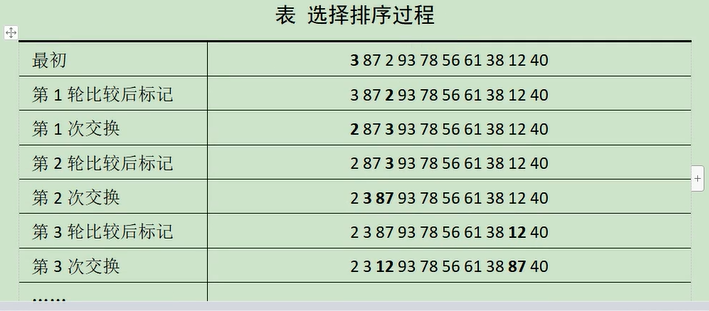
排序算法（简单选择、堆排序、归并）

简单选择排序

排序算法（简单选择、堆排序、归并） ::: tip 简单选择排序原理：将未排序的数组中从前向后遍历，找到最小的元素和数组中第一个元素交换位置，此时数组中第一个元素位置已经确定，再将未排序的数组中从前向后遍历，找到最小的元素和数组中第二个元素交换位置，依次向下。 ::: 排序算法（简单选择、堆排序、归并） 需要两层循环，外层循环控制每一个元素都参与排序，内层循环控制每一个元素确定位置时的比较。 min存放最小元素的下标，每次使用arr[min]和无序数组中每一个元素比较大小，遇到更小的元素时会将更小的元素的下标存放到min中，遍历结束后min中存放着数组中最小的元素下标，将这个元素arr[min]放在无序数组的最前面（和无序数组第一个元素交换），完成一个元素的排序。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>

typedef int Elemtype;
typedef struct
{
    Elemtype* arr;
    int len;
}SSTable;

void InitST(SSTable& ST, int len)
{
    ST.len = len;
    ST.arr = (Elemtype*)malloc(sizeof(Elemtype) * ST.len);
    srand(time(NULL));
    int i;
    for (i = 0; i < ST.len; i++)
    {
        ST.arr[i] = rand() % 100;
    }
}

void Print(SSTable ST)
{
    int i;
    for (i = 0; i < ST.len; i++)
    {
        printf("%3d", ST.arr[i]);
    }
    printf("\n");
}

void swap(int& x, int& y)
{
    int tmp = x;
    x = y;
    y = tmp;
}

void SelectionSort(SSTable& ST)
{
    int i, j;
    for (i = 0; i < ST.len - 1; i++)
    {
        int min = i;  //起始时认为0号元素是最小元素
        for (j = i + 1; j < ST.len; j++)
            //使用数组中i元素之后的每一个元素都和最小元素arr[min]比较，找到最小元素的下标
        {
            if (ST.arr[min] > ST.arr[j])  //当下标为j的元素小于最小元素时
            //将>改成<可以将排序后的数组变为由大到小
            {
                min = j;  //将最小元素的下标min改为j
            }
        }
        if (min != i)
        {
            swap(ST.arr[min], ST.arr[i]);  //同一位置的元素不用交换（交换也不影响）
        }
    }
}

int main()
{
    SSTable ST;
    InitST(ST, 10);
    Print(ST);
    SelectionSort(ST);
    Print(ST);
    return 0;
}

简单选择排序的时间复杂度和空间复杂度

选择排序虽然减少了交换次数，但是循环比较的次数依然和冒泡排序的数量是一样的，都是从1加到N-1，总运行次数为N(N -1)/2。忽略循环内语句的数量，在计算时间复杂度时，主要考虑与N有关的循环，如果循环内交换得多，例如有5条语句，那么最终得到的无非是5n²；循环内交换得少，例如有2条语句，那么得到的就是2n²，但是时间复杂度计算是忽略首项系数的，因此最终还是O(n²)。因此，选择排序的时间复杂度依然为O(n²)。因为未使用额外的空间(额外空间必须与输入元素的个数N相关)，所以空间复杂为O(1)。

堆排序

堆（Heap）是计算机科学中的一种特殊的树状数据结构。若满足以下特性，则可称为堆：“给定堆中任意结点P和C，若P是C的父结点，则P的值小于等于（或大于等于）C的值。”即若父结点的值恒小于等于子结点的值，则该堆称为最小堆(min heap）；反之，若父结点的值恒大于等于子结点的值，则该堆称为最大堆(max heap）。堆中最顶端的那个结点称为根结点( root node），根结点本身没有父结点(parent node）。在工作中将最小堆称为小根堆或小顶堆，把最大堆称为大根堆或大顶堆。

::: tip 堆满足下列性质： 1.堆中某个结点的值总是不大于或不小于其父结点的值； 2.堆总是一棵完全二叉树。 :::

假设有3，87，2，93，78，56，61，38，12，40共10个元素，将这10个元素建成一棵完全二叉树，采用层次建树法，虽然只用一个数组存储元素，但是可以将二叉树中任意一个位置的元素对应到数组下标上。将二叉树中每个元素对应到数组下标的这种数据结构称为堆，比如最后一个父元素的下标是N/2-1，也就是a[4]，对应的值为78。依次将每棵子树都调整为父结点最大，最终将整棵树变为一个大根堆。 ::: warning （完全二叉树在将一个数组调整成一个堆的时候，N为数组长度（下标为0~N-1），最后一个非叶子节点元素的下标是N/2-1。设该节点的数组下标为i，则它的左孩子数组下标为2* i+1，右孩子数组下标为2i+2。分两种情况： ①堆的最后一个非叶子节点只有左孩子。左孩子数组下标为N-1，即N-1=2* i+1，i=N/2-1。 ②堆的最后一个非叶子节点有左右两个孩子。左孩子数组下标为N-2，即N-2=2* i-1，i=(n-1)/2-1；右孩子数组下标为N-1，则N-1=2* i+2，i=(N-1)/2-1） :::

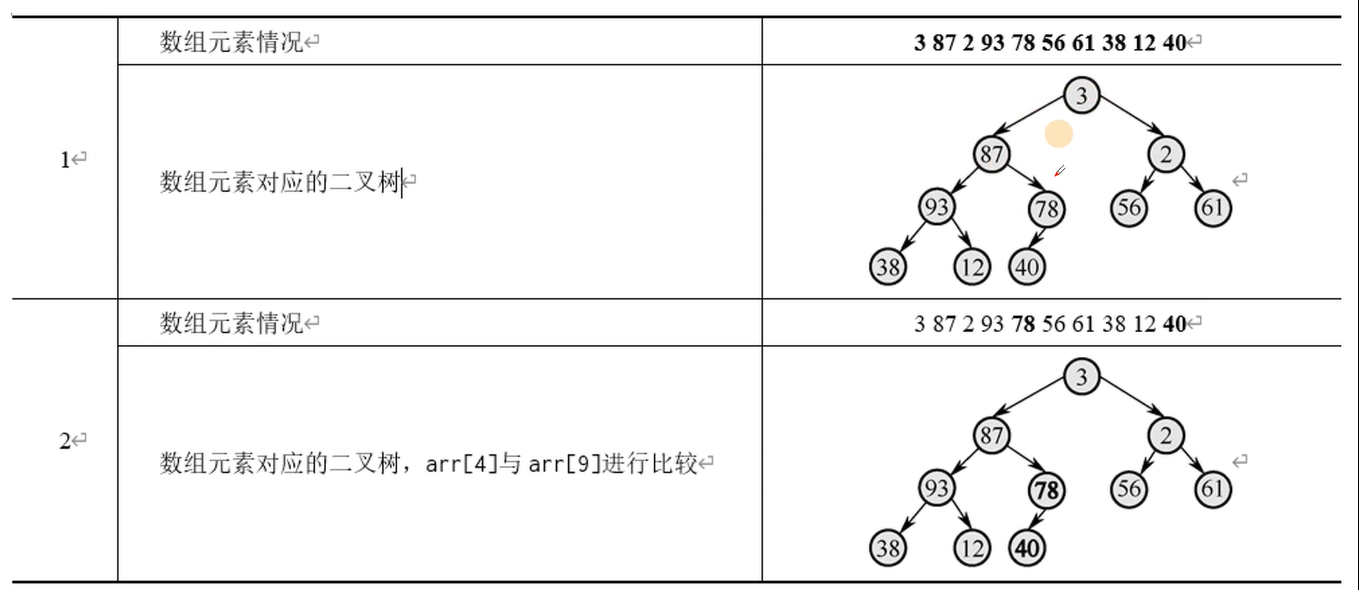
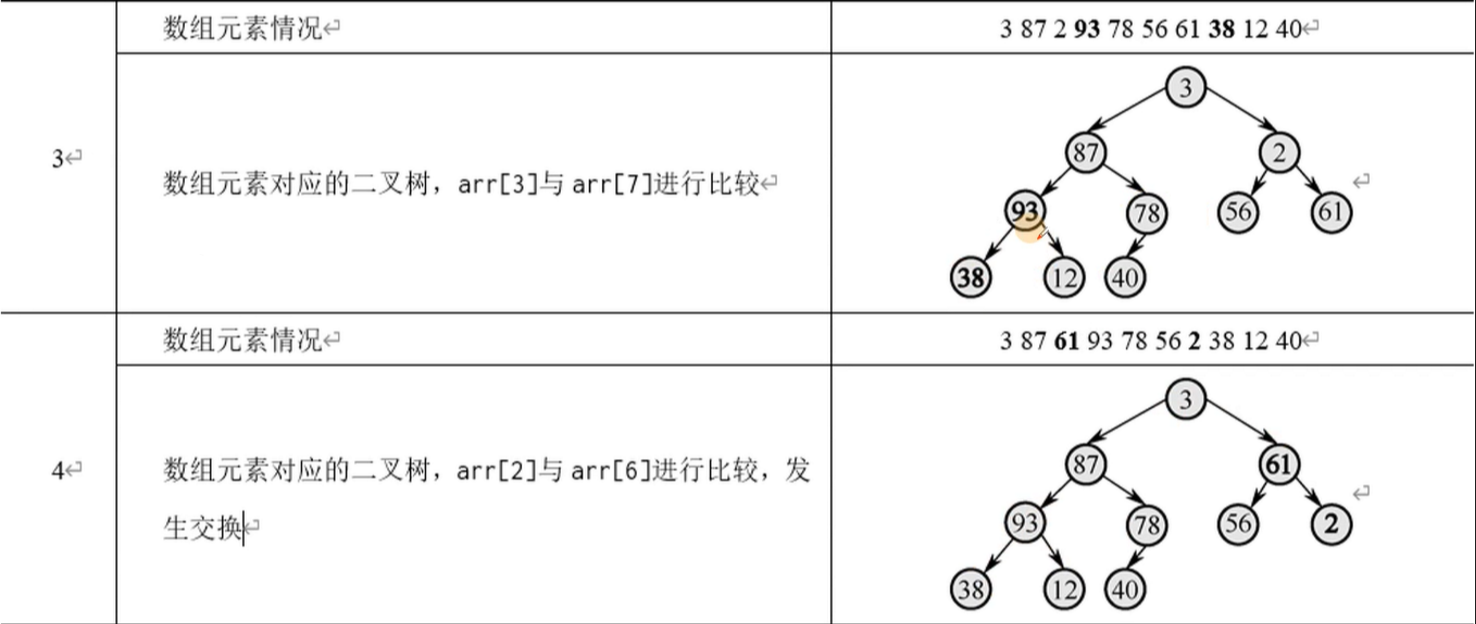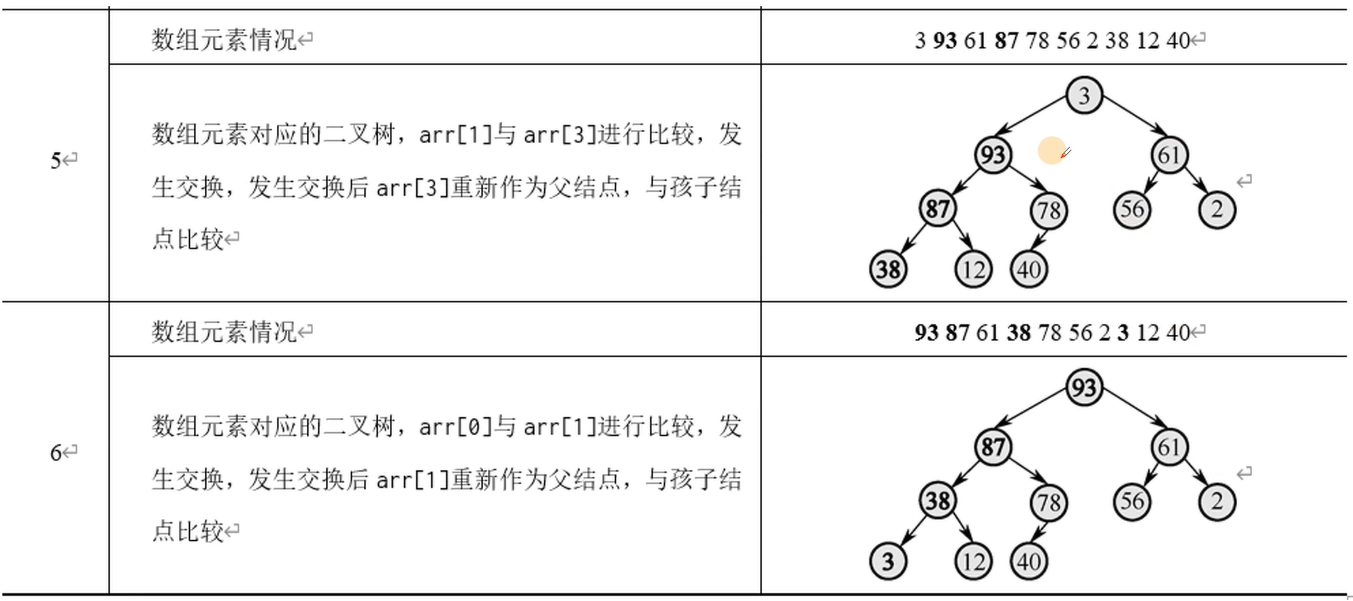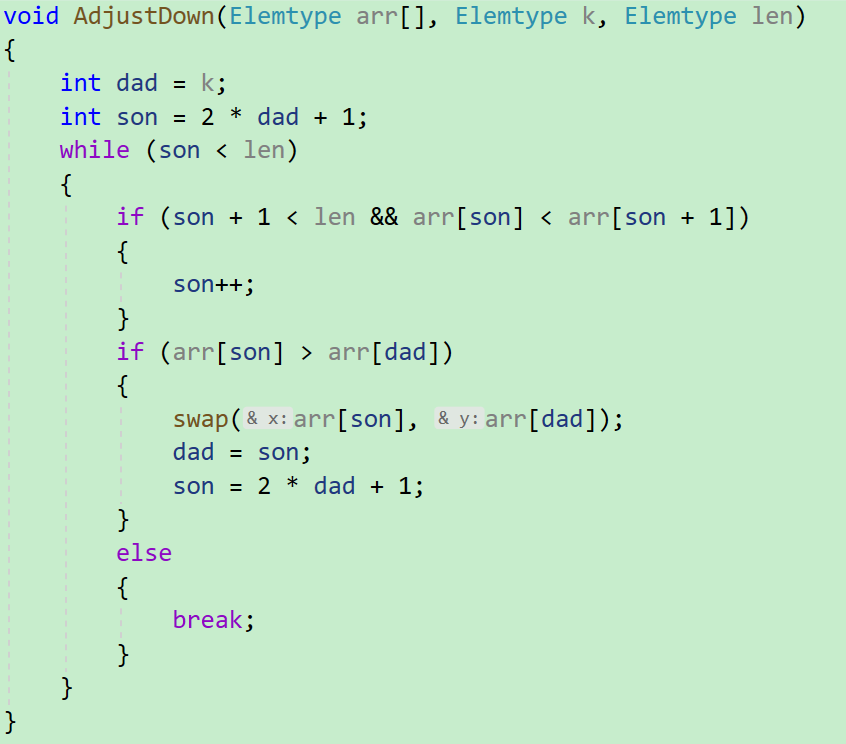
如下图，先将堆调整为一个大顶堆，从最后一个子树开始，将每一个子树调整为大顶堆，整体就会是一个大顶堆。排序算法（简单选择、堆排序、归并）上图中，父节点2的子树不是大顶堆，需要调整，过程是比较左右孩子的大小，将较大的孩子和父节点交换（可以复用之前代码的SWAP函数）。将堆调整为大根堆时，先使用for循环将每一个子树都调整为大根堆。调整过程中每一次孩子节点和父节点交换后，都需要判断新的孩子节点作为下面子树的父节点时是否满足大顶堆的要求，如果不满足，通过循环再做交换。先把根节点和最后一个节点进行交换，即数组0号和9号位置的元素交换，其余元素继续调整为大根堆。再把根节点和最后一个节点进行交换，即数组0号和8号位置的元素交换，数组中最后一个元素已经确定是最大的元素，不再参与调整。依次将元素从大到小在数组中从后往前存放，直到整个数组有序。堆排序函数的代码如下：排序算法（简单选择、堆排序、归并） ::: warning 函数中两个for循环中的变量i代表的含义不同。 ::: 第二个for循环的判断条件可以先假设为i>0，即i最小为1，AdjustDown函数中，dad=0，son=1，len=1，不满足下图AdjustDown函数中的while循环条件son<len，不进入循环。假设i>1，即i最小为2，在AdjustDown函数中，dad=0，son=1，len=2，进入循环后不满足son+1<len，父节点dad下只有一个左孩子，即未排序数组中只剩下两个元素进行比较，即第二个for循环的判断条件i>1成立。排序算法（简单选择、堆排序、归并）

堆排序中AdjustDown结束后需要再执行swap交换，将大根堆中的根节点元素和未排序数组的最后一个元素交换，即把大的元素放在后面。

::: warning 堆排序写代码时应先写一个固定数组进行排序，否则调试难度较大。 :::

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>

typedef int Elemtype;
typedef struct
{
    Elemtype* arr;
    int len;
}SSTable;

void InitST(SSTable& ST, int len)
{
    ST.len = len;
    ST.arr = (Elemtype*)malloc(sizeof(Elemtype) * ST.len);
    srand(time(NULL));
    int i;
    for (i = 0; i < ST.len; i++)
    {
        ST.arr[i] = rand() % 100;
    }
}

void Print(SSTable ST)
{
    int i;
    for (i = 0; i < ST.len; i++)
    {
        printf("%3d", ST.arr[i]);
    }
    printf("\n");
}

void swap(int& x, int& y)
{
    int tmp = x;
    x = y;
    y = tmp;
}

//将某个子树调整为大根堆，需要多次执行（每次只调整一棵子树）
void AdjustDown(Elemtype arr[], Elemtype k, Elemtype len)  //k为要调整的子树的父节点下标，len表示剩余的无序数组的长度
{
    int dad = k;  //要调整的子树的父节点下标
    int son = 2 * dad + 1;  //左孩子下标
    while (son < len)  //当新的父节点产生后，子节点的下标超出数组元素个数时，循环终止
    {
        if (son + 1 < len && arr[son] < arr[son + 1])
        //如果左孩子大于右孩子，下个if判断左孩子是子树中最大的叶子节点，用左孩子和父节点比较
        //存在子树中只有一个子节点的情况，如果不满足son+1<len，说明son指向数组中最后一个元素，该子树没有右孩子
        {
            son++;  //左孩子小于右孩子，进入循环，son++，son变为右孩子
        }
        if (arr[son] > arr[dad])  //右孩子是子树中最大的叶子节点，用右孩子和父节点比较
        {
            swap(arr[son], arr[dad]);  //叶子节点大于父节点，发生交换
            dad = son;  //父节点和子节点发生交换后，检查新的子节点下的子树是否满足大根堆，即将子节点变成父节点继续检查
            son = 2 * dad + 1;  //son变为新的子树左孩子下标
        }
        else
        {
            break;  //父节点和子节点没有发生交换时，即该子树满足大根堆要求，跳出循环，检查其他子树
        }
    }
}

//堆排序
void HeapSort(Elemtype arr[], Elemtype len)
{
    //先把每一个子树调整为大根堆
    int i;
    for (i = len / 2 - 1; i >= 0; i--)  //需要调整的子树的范围是从最后一个非叶子节点（父节点）到根节点
    {
        AdjustDown(arr, i,len);  //i为要调整为大根堆的子树的父节点
    }
    //调整成大根堆后，数组元素仍是无序的
    swap(arr[0], arr[len - 1]);  //交换根节点和最后一个节点元素，确定了最后一个元素位置
    for (i = len - 1; i > 1; i--)  //i表示剩余的无序数组的长度，数组长度-1=数组元素下标
    {
        AdjustDown(arr, 0, i);  //调整剩余元素变为大根堆
        //0表示要调整为大根堆的子树的父节点，每次都是根节点交换位置发生改变，只需要传入根节点下标0
        swap(arr[0], arr[i - 1]);  //交换根节点和最后一个节点元素，确定了最后一个元素位置
        //除最后一个元素，剩余的子树除了根节点所在的子树外都满足大根堆，传入子函数调整
        //根节点调整后，子函数内会依次检查下面调整后每一个不满足大根堆条件的子树，直到生成新的大根堆
        //回到堆排序中的for循环，将此时的大根堆根节点和最后一个节点元素交换，确定最大的一个元素位置，继续循环
    }
}

int main()
{
    SSTable ST;
    InitST(ST, 10);
    //Elemtype A[10] = { 3,87,2,93,78,56,61,38,12,40 };
    //memcpy(ST.arr, A, sizeof(A));
    Print(ST);
    HeapSort(ST.arr,10);
    Print(ST);
    return 0;
}

堆排序的时间复杂度和空间复杂度

AdjustDown函数循环次数是树的高度log2n+1，HeapSort函数的第一个for循环了n/2次，第二个for循环了n次，总计次数是3/2nlog2n次，因此时间复杂度是O(nlog2n)。堆排最好、最坏、平均时间复杂度都是O(nlog2n)。堆排的空间复杂度是O(1)，因为没有使用与n相关的额外空间。

归并排序

归并排序不限制是两两归并还是多个归并。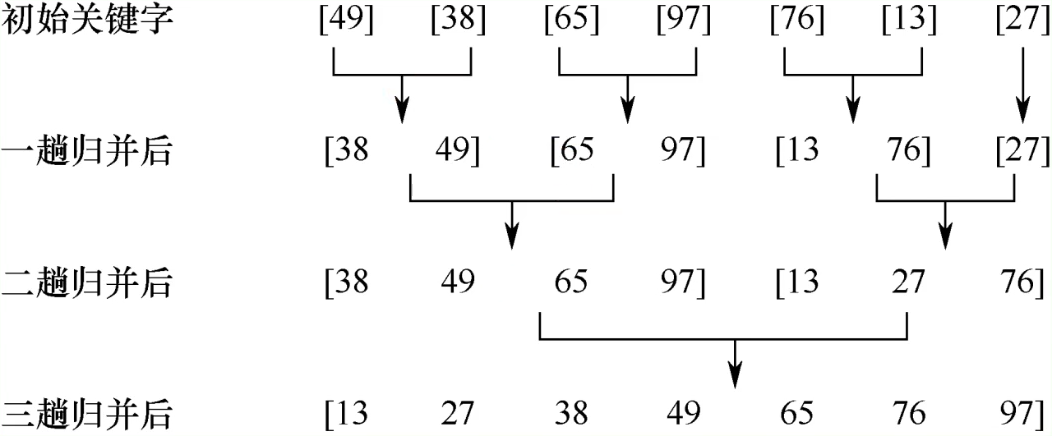排序算法（简单选择、堆排序、归并） ::: tip 两两归并排序原理：如上图把每两个元素归为一组，进行小组内排序，然后再次把两个有序数组合并为一个有序数组，不断进行，最终合并为一个有序数组。每次合并时，将第一个有序数组中的第一个元素和第二个有序数组的所有元素比较大小，确定这个元素的位置后就合并过来，第一个有序数组中的第二个元素继续和第二个有序数组的所有元素比较大小并合并，直到两个有序数组合并成一个有序数组。 ::: ::: warning 归并排序主要用递归写法。代码类似于快速排序。区别是归并排序递归时前一半范围是low到mid，后一半范围是mid+1到high，两次归并排序的元素之间没有空出一个位置，而快速排序需要在中间空出mid的位置。 ::: 排序算法（简单选择、堆排序、归并） 归并排序的核心是Merge合并函数。 合并有序数组时可以不用额外空间，使用额外空间会降低交换次数，业界普遍使用和原有数组一样大的额外空间。

#include <stdio.h>
#include <stdlib.h>
#define N 7  //元素个数
typedef int Elemtype;

//合并两个有序数组（low到mid和mid+1到high）
void Merge(Elemtype arr[], int low, int mid, int high)
{
    static Elemtype arr1[N];  //额外空间和原数组arr一样大
    //static修饰的变量只执行初始化一次，后续递归操作不再执行该语句
    int i, j, k;  //i和j用来遍历数组arr1，k用来遍历arr
    for (i = low; i <= high; i++)
    {
        arr1[i] = arr[i];  //将原数组的元素全部复制到新的数组
        //而后进行比较的数组是新数组arr1，将比较后的结果存在原数组arr中
    }
    k = low;  //k用来依次将排好序的元素放进数组arr中
    //合并两个有序数组
    for (i = low, j = mid + 1; i <= mid && j <= high;)  //i和j分别遍历数组arr1中mid左边和右边的数组，可以将k++放在分号后
    {
        if (arr1[i] < arr1[j])
        {
            arr[k] = arr1[i];  //arr1中mid左边的数组中i位置的元素复制给arr
            i++;  //i指向下一个位置的元素
            k++;  //每次往arr放入一个元素，k都向后移动一个位置
        }
        else  //包括小于等于的情况
        {
            arr[k] = arr1[j];  //arr1中mid右边的数组中j位置的元素复制给arr
            j++;  //j指向下一个位置的元素
            k++;  //每次往arr放入一个元素，k都向后移动一个位置
        }
    }
    //当数组arr1中mid左边或右边的数组先遍历结束，即当i或j不满足判断条件跳出for循环时，可能存在另一半数组中还有元素
    while (i <= mid)
    {
        arr[k] = arr1[i];  //arr1中mid左边的数组剩余元素复制给arr
        i++;
        k++;
    }
    while (j <= high)
    {
        arr[k] = arr1[j];  //arr1中mid右边的数组剩余元素复制给arr
        j++;
        k++;
    }
}
//归并排序
void MergeSort(Elemtype arr[], int low, int high)
{
    if (low < high)
    {
        int mid = (low + high) / 2;
        MergeSort(arr, low, mid);
        MergeSort(arr, mid + 1, high);
        Merge(arr, low, mid, high);
    }
}

void Print(Elemtype* arr)
{
    int i;
    for (i = 0; i < N; i++)
    {
        printf("%3d", arr[i]);
    }
}

int main()
{
    int arr[N] = { 49,38,65,97,76,13,27 };
    MergeSort(arr, 0, 6);  //0和6为数组arr的首元素和末尾元素的下标
    Print(arr);
    return 0;
}

归并排序的时间复杂度和空间复杂度

MergeSort函数的递归次数是log2n，原因是mid = (low + high) / 2，是标准的二分，Merge函数的循环了n次（k从0到n），因此时间复杂度是O(nlog2n)。 ::: tip 二分查找每次剩余一半，对于n个元素的情况：一次二分剩下：n/2 两次二分剩下：n/2/2 = n/4（n/2²） … m次二分剩下：n/(2^m) 在最坏情况下是在排除到只剩下最后一个值之后得到结果，即n/(2^m)=1 所以由上式可得： 2^m=n，进而可求出时间复杂度为： log2(n)。）归并排序最好、最坏、平均时间复杂度都是O(nlog2n)。 ::: 归并排序的空间复杂度是O(n)，因为使用了数组arr1，它的大小与arr一样，占用n个元素的空间。