 一、题目解读
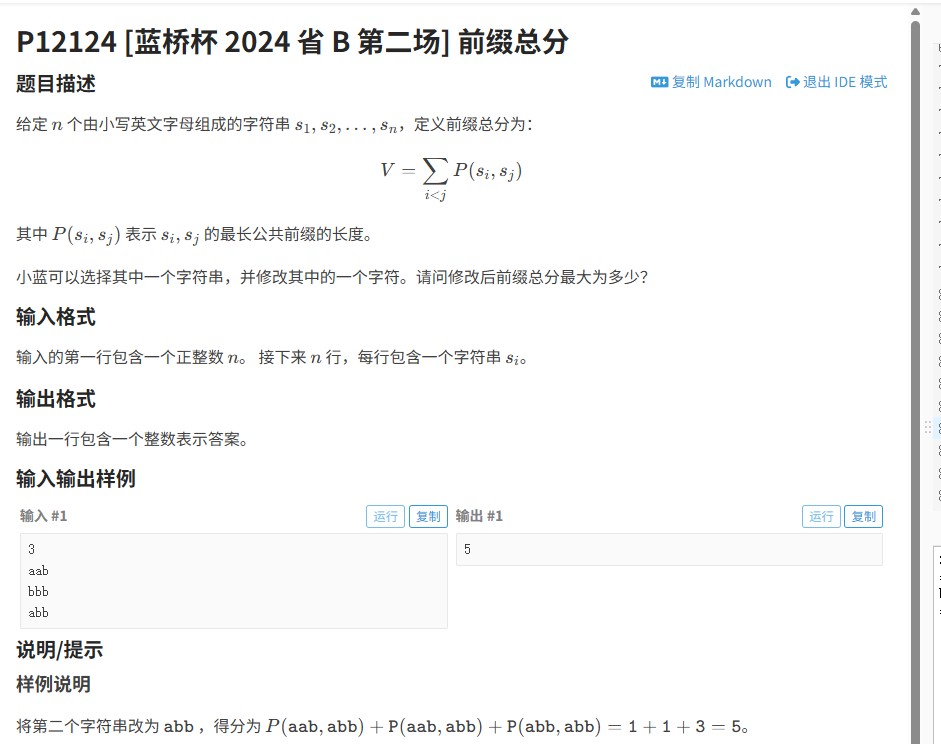
2024年蓝桥杯省B组题目“前缀总分”(对应洛谷P12124)要求计算给定字符串集合中,所有前缀的最长公共前缀(LCP)的总分,并找出通过移动字符位置后可能获得的最大总分。题目考察字符串处理与动态规划能力,需高效计算LCP并优化得分策略。
一、题目解读
2024年蓝桥杯省B组题目“前缀总分”(对应洛谷P12124)要求计算给定字符串集合中,所有前缀的最长公共前缀(LCP)的总分,并找出通过移动字符位置后可能获得的最大总分。题目考察字符串处理与动态规划能力,需高效计算LCP并优化得分策略。
二、解题思路
核心算法:通过预处理计算任意两字符串的LCP,存储于二维矩阵中。
总分计算:利用LCP矩阵,遍历所有字符串对求和。
优化策略:对每个字符位置,迭代替换所有小写字母,动态计算替换后的LCP变化,更新最大得分。
关键逻辑:移动字符仅影响其后的LCP值,通过前缀贡献数组记录原LCP,快速计算替换后的新LCP。
三、解题步骤解析
预处理LCP矩阵:
双循环遍历字符串对,逐字符比较直至不同,记录LCP值并对称填充矩阵。
初始总分计算:
利用LCP矩阵,累加所有非对角线元素得到原始总分。
迭代优化得分:
遍历每个字符串的每个字符位置,替换为其他小写字母。
计算替换后的新LCP:仅考虑当前位置及之后字符的贡献,利用前缀贡献数组加速。
更新总分差值,取最大值。
四、代码与注释
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
// 预处理LCP矩阵
vector<vector<int>> precompute_lcp(const vector<string>& strs) {
int n = strs.size();
vector<vector<int>> lcp(n, vector<int>(n, 0));
for (int i = 0; i < n; ++i) {
for (int j = i+1; j < n; ++j) {
int len = 0;
while (len < strs[i].size() && len < strs[j].size() && strs[i][len] == strs[j][len]) {
len++;
}
lcp[i][j] = lcp[j][i] = len; // 对称赋值
}
}
return lcp;
}
// 计算LCP总分
long long compute_total(const vector<vector<int>>& lcp) {
long long total = 0;
int n = lcp.size();
for (int i = 0; i < n; ++i) {
for (int j = i+1; j < n; ++j) {
total += lcp[i][j];
}
}
return total;
}
// 主解题函数
long long solve(vector<string>& strs) {
int n = strs.size();
auto lcp = precompute_lcp(strs); // 预处理
long long original = compute_total(lcp); // 原始总分
long long max_score = original; // 初始化最大值
for (int i = 0; i < n; ++i) {
string original_str = strs[i]; // 当前字符串
vector<int> original_contrib(n, 0); // 记录原LCP贡献
for (int j = 0; j < n; ++j) {
if (j!= i) original_contrib[j] = lcp[i][j]; // 非自身贡献
}
for (int pos = 0; pos < original_str.size(); ++pos) { // 遍历字符位置
char original_char = original_str[pos];
for (char c = 'a'; c <= 'z'; ++c) { // 替换为其他字母
if (c == original_char) continue;
long long delta = 0; // 总分差值
for (int j = 0; j < n; ++j) {
if (j == i) continue; // 跳过自身
int new_len = min(original_contrib[j], pos); // 替换后的前缀长度
if (new_len == pos) {
while (new_len < strs[i].size() && new_len < strs[j].size()) {
if (strs[i][new_len]!= c || strs[j][new_len]!= c) break;
new_len++; // 扩展新LCP
}
}
delta += new_len - original_contrib[j]; // 累加差值
}
max_score = max(max_score, original + delta); // 更新最大值
}
}
}
return max_score;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
int n; cin >> n;
vector<string> strs(n);
for (int i = 0; i < n; ++i) cin >> strs[i];
cout << solve(strs) << endl;
return 0;
}注释说明:
通过precompute_lcp高效计算LCP矩阵,减少重复计算。
compute_total利用矩阵非对角线元素求和。
主函数迭代每个字符位置替换,动态计算新LCP并累加差值,维持最大值。五、总结 该解法通过预处理LCP矩阵降低时间复杂度,结合动态规划思想迭代字符替换,高效求解最大总分。核心在于理解LCP对总分的影响范围(仅后续字符),并通过前缀贡献数组优化替换后的LCP计算。算法复杂度主要集中于预处理(O(N^2 * M))和迭代替换(O(N * M * |Σ|)),适用于中小规模数据场景。