一、题目解读
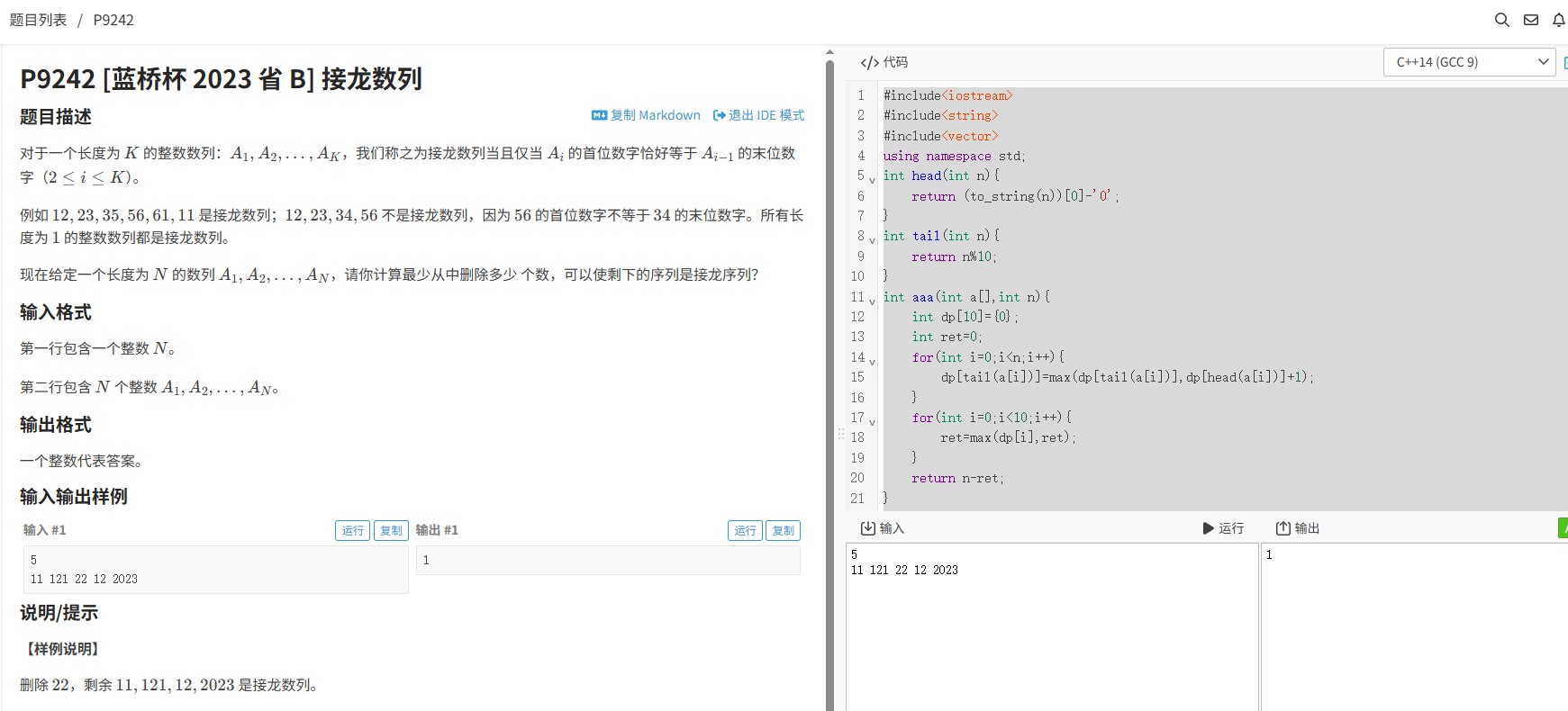
这道蓝桥杯省赛真题要求找出数字序列中最长的接龙子序列(每个数字的首位等于前一个数字的末位),并计算需要删除的最少数字个数。题目考察动态规划的实际应用能力,是理解数字特征处理和状态转移的典型案例。
二、解题步骤
1.处理n=1的特殊边界情况
2.读取输入数字序列
3.初始化dp数组(大小为10,对应0-9的数字)
4.遍历数字序列:
获取当前数字的首位和末位
更新dp[末位]的值
5.找出dp数组中的最大值
6.计算并输出需要删除的数字个数
三、代码实现(带注释)
#include<iostream>
#include<string>
#include<vector>
using namespace std;
// 获取数字首位
int head(int n){
return (to_string(n))[0]-'0';
}
// 获取数字末位
int tail(int n){
return n%10;
}
// 核心计算函数
int aaa(int a[],int n){
int dp[10]={0}; // dp数组,索引表示数字末位
int ret=0;
for(int i=0;i<n;i++){
dp[tail(a[i])]=max(dp[tail(a[i])],dp[head(a[i])]+1);
}
for(int i=0;i<10;i++){
ret=max(dp[i],ret); // 找出最长序列
}
return n-ret; // 计算需要删除的数字个数
}
int main(){
int n;
cin>>n;
if(n==1){ // 特殊情况处理
cout<<0;
return 0;
}
int a[100005];
for(int i=0;i<n;i++){
cin>>a[i]; // 读取输入
}
cout<<aaa(a,n);
return 0;
}