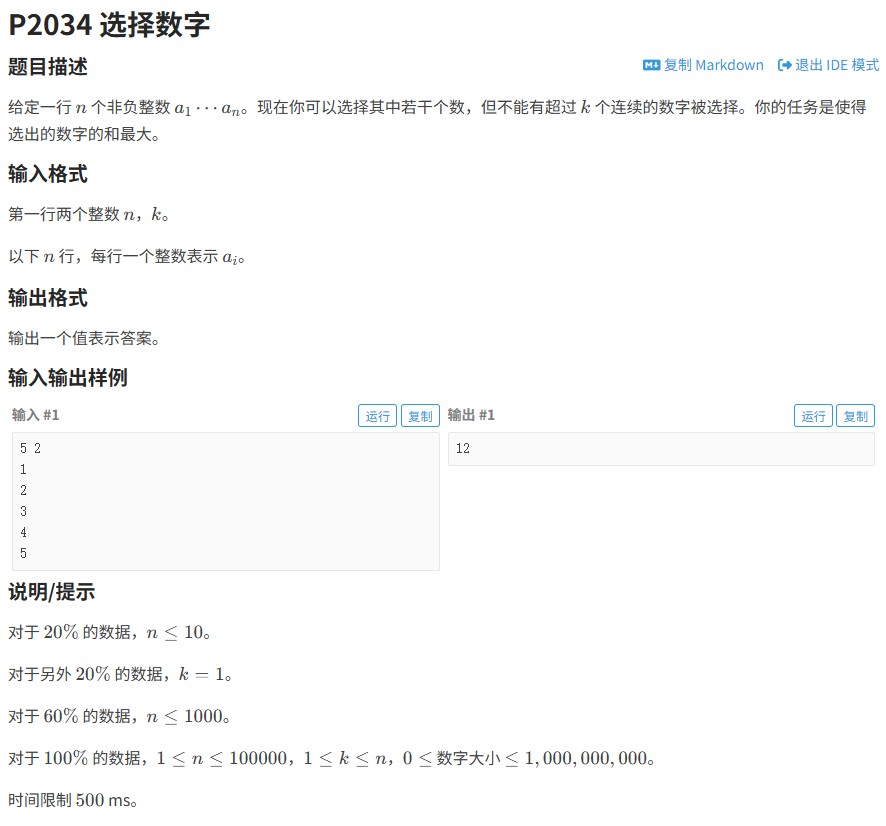
一、题目解读 洛谷P2034题目要求给定一个长度为n的整数数组，将其分成不超过k段，求各段和的最大值。该问题属于经典动态规划问题的扩展，需结合优化技巧高效求解。

二、解题思路 采用动态规划+单调队列优化的策略。核心思想是定义状态dp[i]表示前i个数分成不超过k段的最大和，通过维护单调队列优化决策点选择。关键在于利用前缀和计算子段和，并通过队列动态维护合法且最优的决策点，避免暴力枚举导致的超时。

三、解题步骤

1. 前缀和计算：预处理数组前缀和prefix，方便O(1)获取任意区间和。

2. 动态规划初始化：初始化dp[0]=0，表示不选任何数的和为0。

3. 状态转移：遍历i=1~n+1时，通过队列头部元素j计算dp[i] = dp[j] + prefix[i-1] - prefix[j]，即前j个数分成k段的最大和 + 剩余部分。

4. 队列维护：

   弹出队首不符合区间限制的元素（i-j-1 > k）；

   弹出队尾使dp[i]-prefix[i] >= dp[q.back()]-prefix[q.back()]的元素，确保队列单调递增。

5. 结果：最终dp[n+1]即为答案。

四、代码与注释

#include <iostream>
#include <vector>
#include <deque>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr); // 加快输入输出速度

    int n, k;
    cin >> n >> k;
    vector<long long> a(n + 1), prefix(n + 1, 0);
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        prefix[i] = prefix[i - 1] + a[i]; // 计算前缀和
    }

    vector<long long> dp(n + 2, 0); // dp[i]表示前i个数的最大和
    deque<int> q; // 单调队列维护最优决策点

    // 初始条件：不选任何数时和为0
    q.push_back(0);

    for (int i = 1; i <= n + 1; ++i) {
        // 维护队列头部，确保不超过k的限制
        while (!q.empty() && q.front() < i - k - 1) {
            q.pop_front();
        }

        // 状态转移：dp[i] = max(dp[j-1] - prefix[j]) + prefix[i-1]
        dp[i] = dp[q.front()] + prefix[i - 1] - prefix[q.front()];

        // 维护队列单调性
        while (!q.empty() && dp[i] - prefix[i] >= dp[q.back()] - prefix[q.back()]) {
            q.pop_back();
        }

        q.push_back(i);
    }

    cout << dp[n + 1] << endl;
    return 0;
}

五、总结 本解法通过动态规划将问题转化为子问题最优解的组合，利用单调队列优化决策点选择，将时间复杂度降至O(n)，成功解决洛谷P2034的挑战。该思路对处理分段优化类问题具有重要参考价值，体现了算法设计与数据结构的巧妙结合。 参考：洛谷题