 一、题目解读
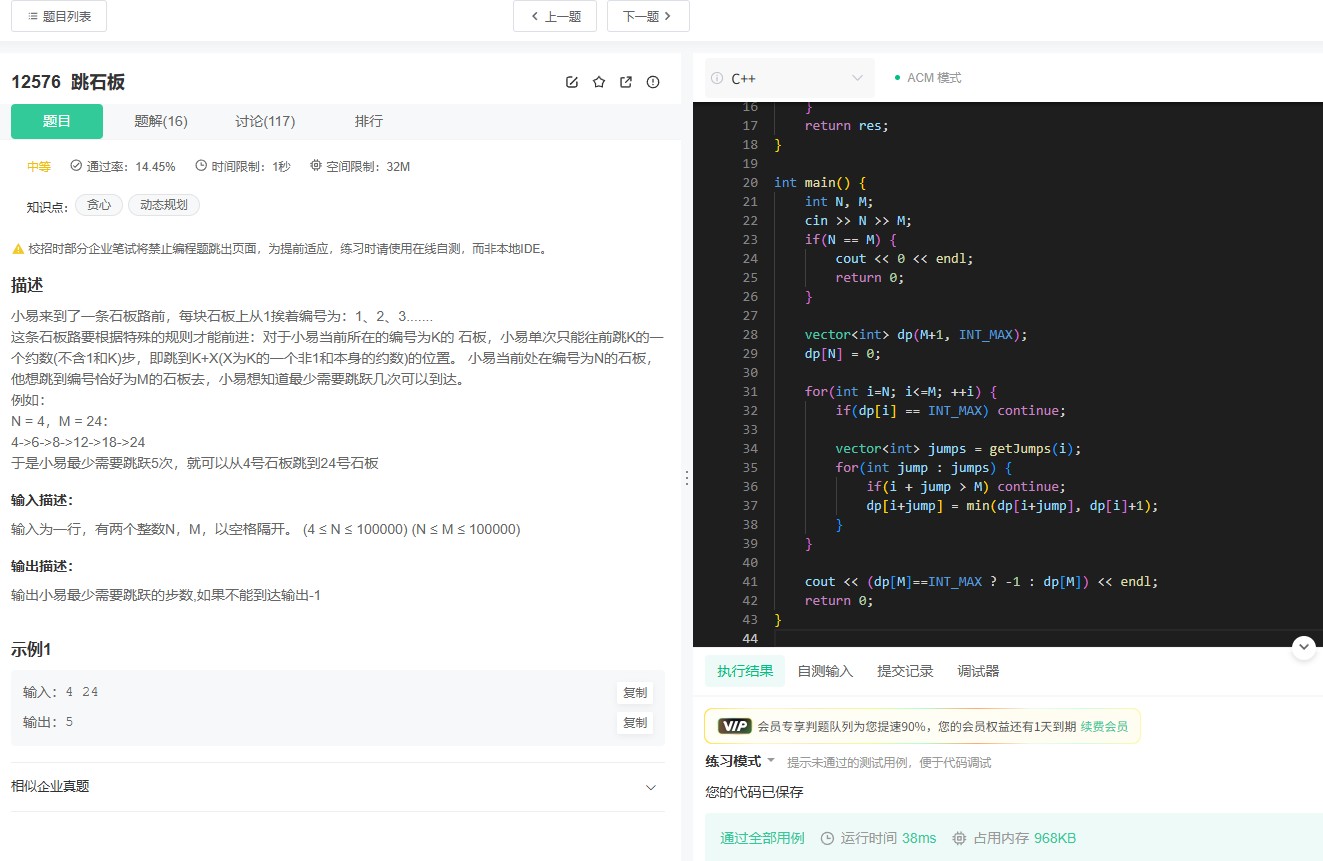
牛客12576题是一道经典的算法题,要求给定起点N和终点M,求解从N到M的最少跳跃次数。题目考察的核心在于路径优化与动态规划思想,需结合数论中的质因数分解技巧,通过合理设计算法降低时间复杂度,避免暴力枚举的指数级耗时。
一、题目解读
牛客12576题是一道经典的算法题,要求给定起点N和终点M,求解从N到M的最少跳跃次数。题目考察的核心在于路径优化与动态规划思想,需结合数论中的质因数分解技巧,通过合理设计算法降低时间复杂度,避免暴力枚举的指数级耗时。
二、解题思路 采用“动态规划+质因数分解”的双重优化策略。首先,通过质因数分解函数getJumps()高效获取每个数的跳跃因子(即质因数),避免对非质因数位置的无效计算。随后,利用动态规划数组dp[]记录各节点的最小跳跃次数,从起点N递推至终点M,通过状态转移方程dp[i+jump] = min(dp[i+jump], dp[i]+1)实现路径优化。特别处理了N=M的边界情况,以及跳跃超出范围时的剪枝,确保代码高效且逻辑严谨。
三、解题步骤详解 1. 预处理质因数:调用getJumps()函数,通过筛选法仅对平方数以内的候选数进行试除,若找到质因数i及其对应的补数n/i(当i≠n/i时),则将其加入跳跃列表。 2. 初始化动态规划:创建dp数组,初始值设为INT_MAX,表示未访问状态。起点N赋值为0,作为递推基准。 3. 递推更新路径:从N开始正向迭代,仅对已计算的最小步数节点(dp[i]≠INT_MAX)扩展。遍历该节点的跳跃列表,计算可达位置i+jump,若未超界则更新dp值。 4. 输出结果:最终判断dp[M]是否可达,若为INT_MAX则输出-1,否则输出最小步数。
四、代码及注释
#include <iostream>
#include <vector>
#include <climits>
#include <algorithm>
using namespace std;
// 质因数分解函数:获取数n的所有跳跃因子(质因数)
vector<int> getJumps(int n) {
vector<int> res;
if(n <= 1) return res; // 边界处理:1及以下无需分解
for(int i=2; i*i<=n; ++i) { // 优化:仅遍历至√n
if(n%i == 0) { // 若i是质因数
res.push_back(i);
if(i!= n/i) res.push_back(n/i); // 补数非自身时加入(避免重复)
}
}
return res;
}
int main() {
int N, M; // 输入起点和终点
cin >> N >> M;
if(N == M) { // 边界特判:起点=终点无需跳跃
cout << 0 << endl;
return 0;
}
vector<int> dp(M+1, INT_MAX); // 动态规划数组,初始化为最大值
dp[N] = 0; // 起点步数为0
for(int i=N; i<=M; ++i) { // 正向迭代扩展
if(dp[i] == INT_MAX) continue; // 跳过未访问节点
vector<int> jumps = getJumps(i); // 获取当前节点的跳跃列表
for(int jump : jumps) { // 遍历跳跃因子
if(i + jump > M) continue; // 剪枝:超出终点范围不更新
dp[i+jump] = min(dp[i+jump], dp[i]+1); // 状态转移:更新最小步数
}
}
cout << (dp[M]==INT_MAX? -1 : dp[M]) << endl; // 输出结果或不可达标记
return 0;
}