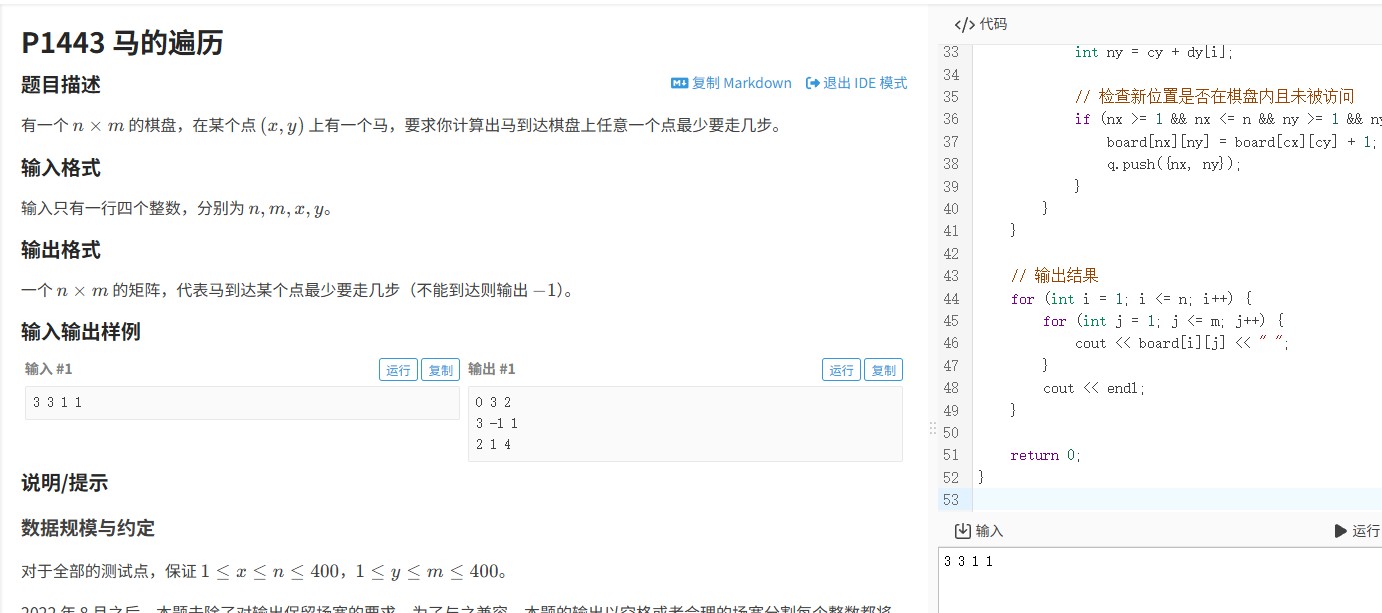
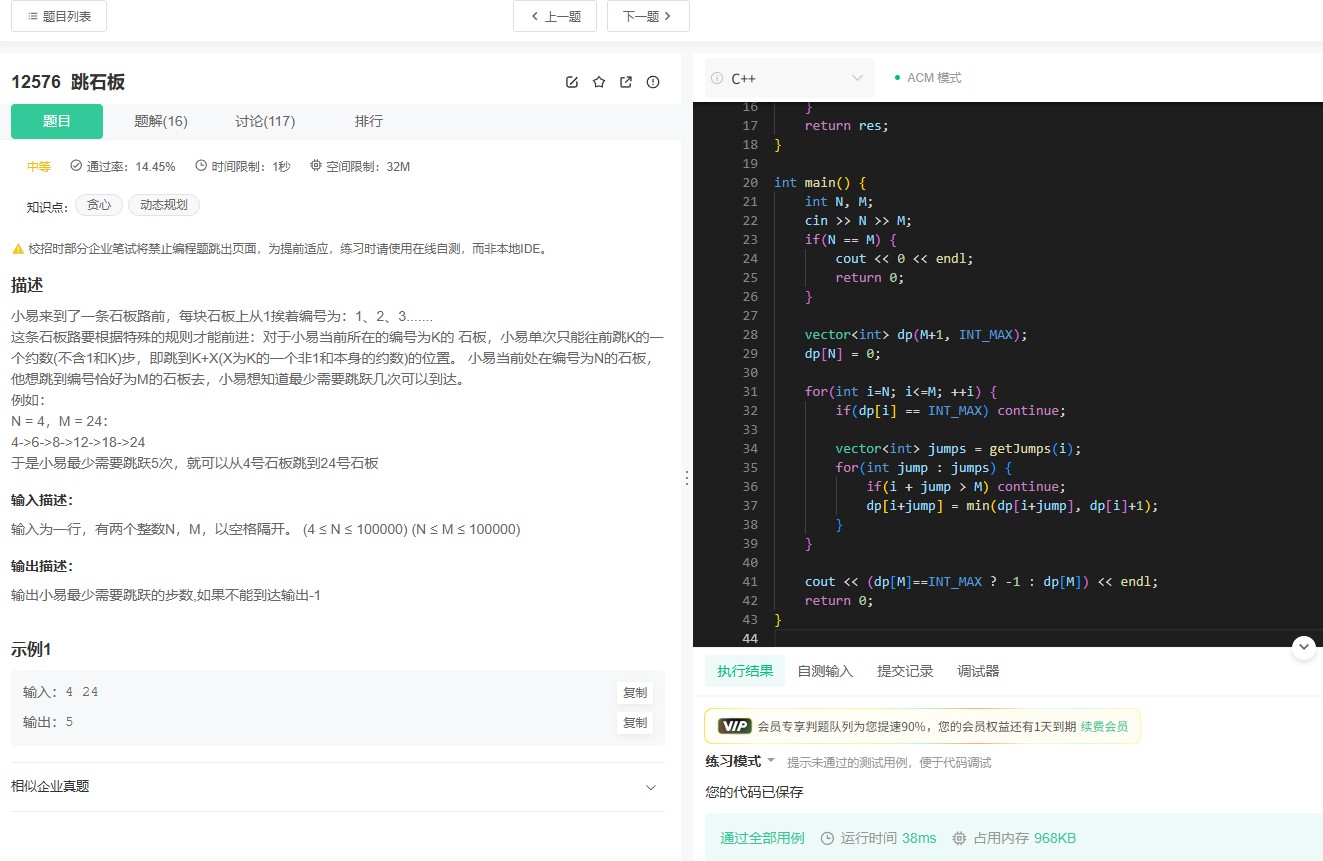
一、题目重述 给定n×m的二维矩阵表示探险地图，每个格子可能是： 平地（'.'） 障碍物（'#'） 起点（'S'） 终点（'E'） 求从起点到终点的最短路径步数，无法到达则输出-1。 二、核心算法：BFS广度优先搜索 选择原因：BFS是解决无权图最短路径问题的最优方案，时间复杂度O(nm)完全适合题目约束条件（典型n,m≤1000）

二、完整C++实现（带详细注释）

#include <bits/stdc++.h>
using namespace std;

const int N = 1005;
char grid[N][N];
int dist[N][N]; // 距离矩阵
int n, m;
int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, -1, 1}; // 方向数组

int bfs(int sx, int sy, int ex, int ey) {
    memset(dist, -1, sizeof dist);
    queue<pair<int,int>> q;
    q.push({sx, sy});
    dist[sx][sy] = 0;

    while (!q.empty()) {
        auto [x, y] = q.front();
        q.pop();

        for (int i = 0; i < 4; i++) {
            int nx = x + dx[i], ny = y + dy[i];
            // 越界检查 || 障碍物检查 || 已访问检查
            if (nx < 0 || nx >= n || ny < 0 || ny >= m 
                || grid[nx][ny] == '#' || dist[nx][ny] != -1) 
                continue;

            dist[nx][ny] = dist[x][y] + 1;
            if (nx == ex && ny == ey) return dist[nx][ny];
            q.push({nx, ny});
        }
    }
    return -1;
}

int main() {
    cin >> n >> m;
    int sx, sy, ex, ey;

    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
            if (grid[i][j] == 'S') sx = i, sy = j;
            if (grid[i][j] == 'E') ex = i, ey = j;
        }

    cout << bfs(sx, sy, ex, ey);
    return 0;
}

四、算法优化点 双向BFS：当起点和终点都已知时，可减少50%搜索范围 A*算法：若有启发式信息可用（如坐标距离） 输入优化：使用快速IO方法处理大规模数据

原文：洛谷P11228地图探险题解（CSP-J 2024真题）