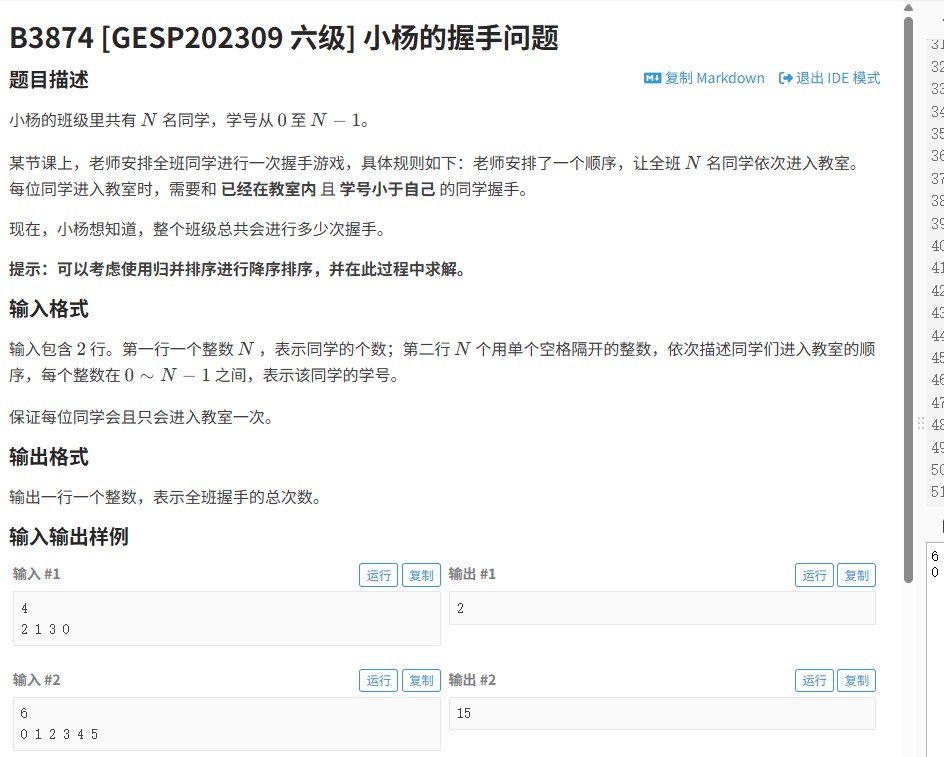
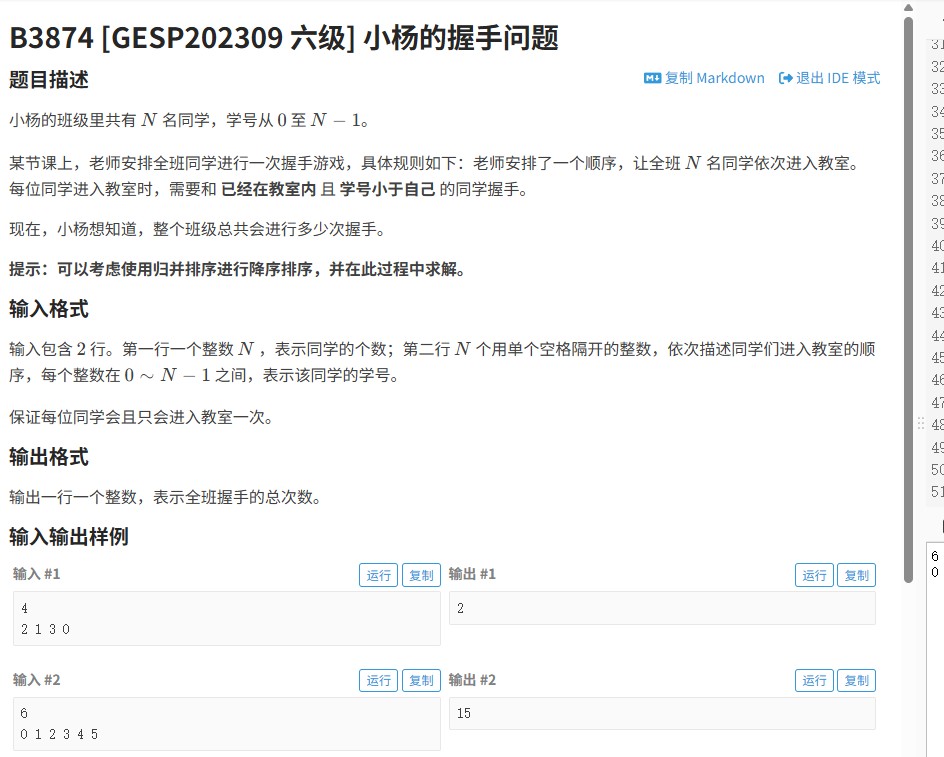
一、题目解读 “小杨的握手问题”源自2023年GESP六级考试（对应洛谷题目B3874）。题目描述为：给定一个长度为N的排列，每次将当前数与之前未访问过的数握手，求总共握手次数。本质上是求排列中逆序对的个数，即统计每个数右侧比它小的元素数量。需设计高效算法在O(NlogN)时间内解决。

二、解题思路 核心思想是将握手次数转化为逆序对计数问题，利用Fenwick树（二叉索引树）实现动态区间查询与更新。通过维护数组元素的顺序统计信息，每次查询当前数之前已出现数的个数，即为该数的握手次数。关键在于将离散的握手操作转化为可差分维护的区间操作，避免暴力枚举。

三、解题步骤

1. 数据预处理：将输入数据转换为1-based索引（原代码中通过order[i]++实现），便于Fenwick树操作。

2. 构建Fenwick树：初始化大小为N的树，初始值全为0。

3. 逆序对统计：

   1.遍历排列顺序，对于每个数current：

   2.查询ft.query(current-1)：获取当前位置前比current小的元素个数（即左侧逆序对）。

   3.更新ft.update(current,1)：将current加入树中，标记已访问。

4. 累计握手次数：将每次查询结果累加至handshakes变量。

5. 输出结果：最终handshakes即为总握手次数。

四、代码与注释

#include <iostream>
#include <vector>
using namespace std;

class FenwickTree {
private:
   vector<int> tree;
   int size;
public:
   FenwickTree(int n) : size(n), tree(n + 1, 0) {} // 构造函数初始化树大小及全0数组

   void update(int index, int delta) {
       for(; index <= size; index += index & -index) // 从index到末尾更新，利用二进制位操作
           tree[index] += delta;
   }

   int query(int index) {
       int res = 0;
       for(; index > 0; index -= index & -index) // 从index到1查询，逐步累加
           res += tree[index];
       return res;
   }
};

int main() {
   ios::sync_with_stdio(false);
   cin.tie(nullptr); // 加快输入输出速度

   int N;
   cin >> N;
   vector<int> order(N);
   for(int i = 0; i < N; i++) {
       cin >> order[i];
       order[i]++; // 转换为1-based索引，适配Fenwick树操作
   }

   FenwickTree ft(N);
   long long handshakes = 0;

   for(int i = 0; i < N; i++) {
       int current = order[i];
       handshakes += ft.query(current - 1); // 查询比current小的已存在数个数
       ft.update(current, 1); // 标记当前数已出现
   }

   cout << handshakes << endl;
   return 0;
}

五、总结 本解法通过将握手问题转化为逆序对计数，利用Fenwick树的O(logN)区间查询与更新，实现高效求解。相较于暴力或归并排序等算法，Fenwick树具有代码简洁、常数优化的优势，尤其在处理动态统计问题时表现优异。掌握此类数据结构的应用，对算法竞赛与实际问题求解具有重要意义。 原文：2023年GESP六级小杨握手问题（洛谷B3874）：Fenwick树求解逆序对的代码解析