2023年 GESP六级小杨的握手问题的优雅解法：树状数组实战

一、问题背景与算法选择

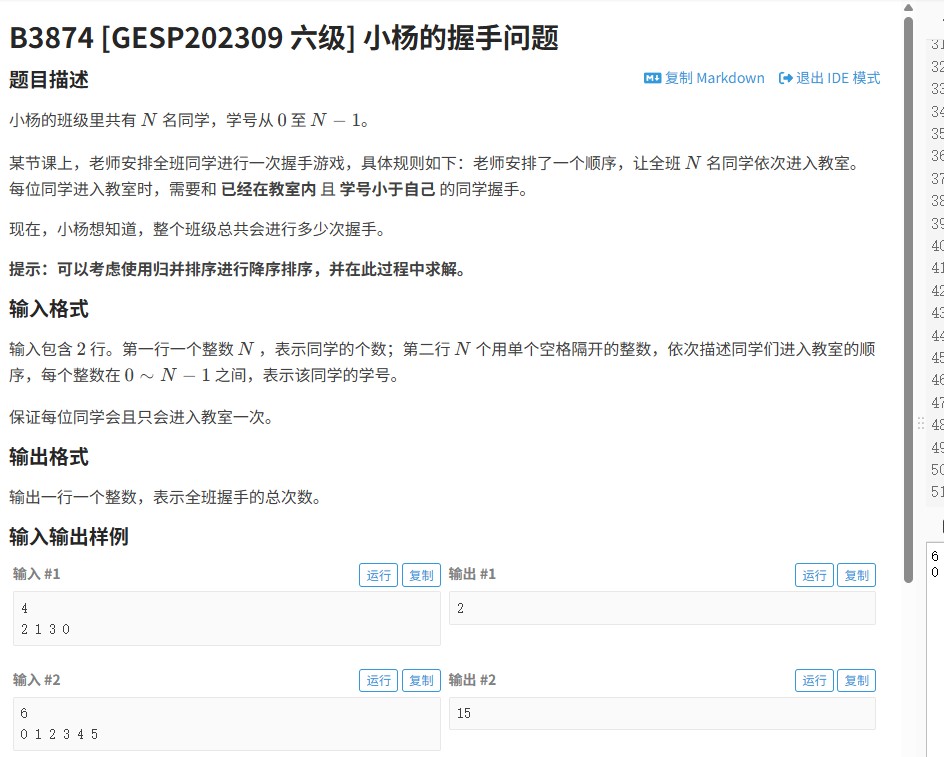
题目要求计算n个人按照特定顺序排队时发生的握手次数，本质上是计算序列中逆序对的数量。树状数组(Fenwick Tree)因其高效的区间查询和单点更新能力(O(logn))成为解决此类问题的理想选择。

二、完整代码实现（带详细注释）

#include <iostream>
#include <vector>
using namespace std;

// 树状数组实现类 
class FenwickTree { 
private: 
    vector tree; // 存储树状数组 
    int size; // 数组大小 
public: 
    // 构造函数，初始化大小为n的树状数组 
    FenwickTree(int n) : size(n), tree(n + 1, 0) {}
    // 更新操作：在index位置增加delta
    void update(int index, int delta) {
        // 典型的树状数组更新方式
        for(; index <= size; index += index & -index)
            tree[index] += delta;
    }

    // 查询操作：求前index个元素的和
    int query(int index) {
        int res = 0;
    // 典型的树状数组查询方式
        for(; index > 0; index -= index & -index)
            res += tree[index];
        return res;
    }
};
int main() { 
    // 优化输入输出 
    ios::sync_with_stdio(false); 
    cin.tie(nullptr);
    int N;
    cin >> N;
    vector<int> order(N);
    for(int i = 0; i < N; i++) {
        cin >> order[i];
        order[i]++; // 转换为1-based索引
    }

    // 初始化树状数组
    FenwickTree ft(N);
    long long handshakes = 0;

    // 核心计算逻辑
    for(int i = 0; i < N; i++) {
        int current = order[i];
        // 查询比current小的已存在数的个数
        handshakes += ft.query(current - 1);
        // 将当前数加入树状数组
        ft.update(current, 1);
    }

    cout << handshakes << endl;
    return 0;
}