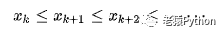一、算法思路

波动数列是蓝桥杯经典赛题，要求计算满足特定条件的数列数量。本文将详细解析动态规划解法，帮助算法初学者掌握状态设计和转移技巧。

二、完整代码

#include <iostream>
#include <vector>
using namespace std;

const int MOD = 100000007;

// 自定义取模函数处理负数
inline int mod(int x, int n) {
    return (x % n + n) % n;
}

int main() {
    int n, s, a, b;
    cin >> n >> s >> a >> b;

    // dp[i][j]表示前i项的和模n等于j的方案数
    vector<vector<int>> dp(n, vector<int>(n, 0));
    dp[0][0] = 1;  // 初始状态：0项和为0有1种方案

    for (int i = 1; i < n; i++) {
        for (int j = 0; j < n; j++) {
            // 状态转移：当前项可以+a或-b
            dp[i][j] = (dp[i-1][mod(j - a*i, n)] + dp[i-1][mod(j + b*i, n)]) % MOD;
        }
    }

    // 输出结果：满足s ≡ sum mod n的方案数
    cout << dp[n-1][mod(s, n)] << endl;
    return 0;
}

三、关键算法解析

1. 问题建模：
2. • 将数列视为每次选择+a或-b的决策序列
   • 利用模运算缩小状态空间
3. 动态规划设计：
4. • 状态定义：dp[i][j]表示前i项和模n等于j的方案数
   • 初始状态：dp[0][0] = 1（空序列和为0）
   • 状态转移：考虑+ai和-bi两种情况
5. 负数处理技巧：
6. • 自定义mod函数处理负数取模
   • 确保数组索引始终有效

四、常见问题解答

Q：为什么要使用模运算？ A：模运算可以大幅缩小状态空间，将无限可能转化为有限状态。

Q：状态转移方程如何理解？ A：当前状态值来自两种选择方案数的和：前一步选择+a或前一步选择-b。

Q：如何处理大数问题？ A：每一步都取模，防止数值溢出并符合题目要求。

来源：竞赛资料