一、问题描述与递推关系建立

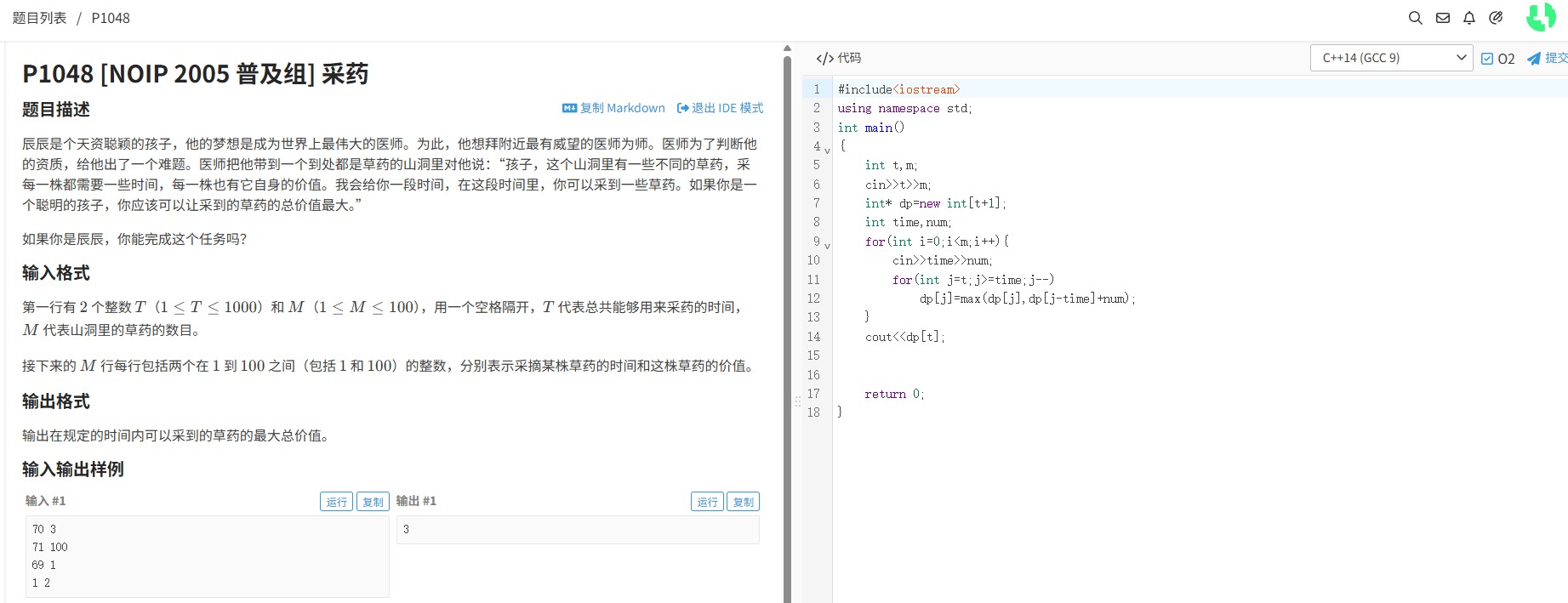
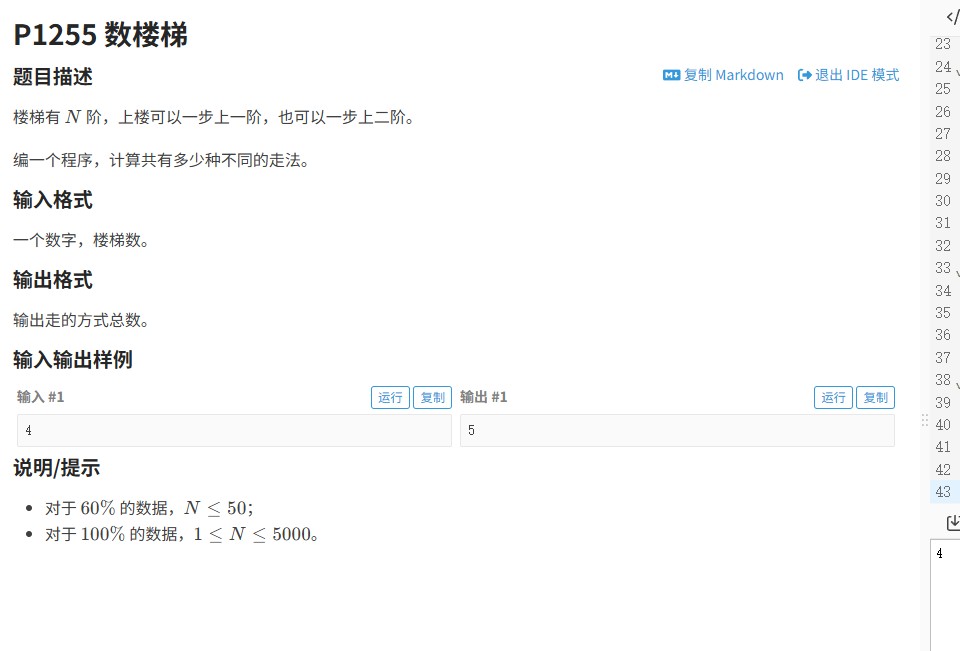
洛谷P1255数楼梯问题要求计算n级台阶的不同走法数，每次可以跨1级或2级。这本质上是斐波那契数列的变种问题，递推公式为f(n)=f(n-1)+f(n-2)。当n≤50时可用普通整型存储，但题目中n可能达到5000，这就必须使用高精度运算来处理大数。为什么说这个问题需要特殊处理呢？因为普通数据类型的存储范围根本无法容纳如此大的数值。我们需要建立清晰的递推思维：第n级台阶的走法数等于从n-1级跨1步上来，加上从n-2级跨2步上来的走法数之和。

二、完整C++代码实现

#include <iostream>
#include <vector>
using namespace std;

// 高精度加法（逆序存储的数字）
vector<int> add(vector<int>& a, vector<int>& b) {
    vector<int> c;
    int carry = 0;
    for(int i = 0; i < a.size() || i < b.size() || carry; i++) {
        if(i < a.size()) carry += a[i];
        if(i < b.size()) carry += b[i];
        c.push_back(carry % 10);
        carry /= 10;
    }
    return c;
}

int main() {
    int n;
    cin >> n;

    // 边界条件处理
    if(n == 0) {
        cout << 0;
        return 0;
    }

    // 初始化滚动数组（逆序存储：个位在[0]）
    vector<int> f[3] = {{1}, {1}, {}};

    // 动态规划递推
    for(int i = 2; i <= n; i++) {
        f[i%3] = add(f[(i-1)%3], f[(i-2)%3]);
    }

    // 逆序输出结果
    for(int i = f[n%3].size()-1; i >= 0; i--) {
        cout << f[n%3][i];
    }
    return 0;
}

三、代码关键点解析

代码中高精度加法的实现采用vector容器存储数字各位，通过carry变量处理进位。主函数中使用f[3]的滚动数组来优化空间，模3运算实现状态轮转。边界条件n=0时需要特殊处理，因为题目规定楼梯级数从0开始。输出时要注意数字是逆序存储的，所以需要从高位到低位反向输出。为什么采用%3的模运算？这创造了一个循环使用的存储空间，三个位置足够存储当前需要的三个连续状态，实现了空间复用。

原文：洛谷P1255题 解题思路和步骤 C++实现带注释,c++入门基础题