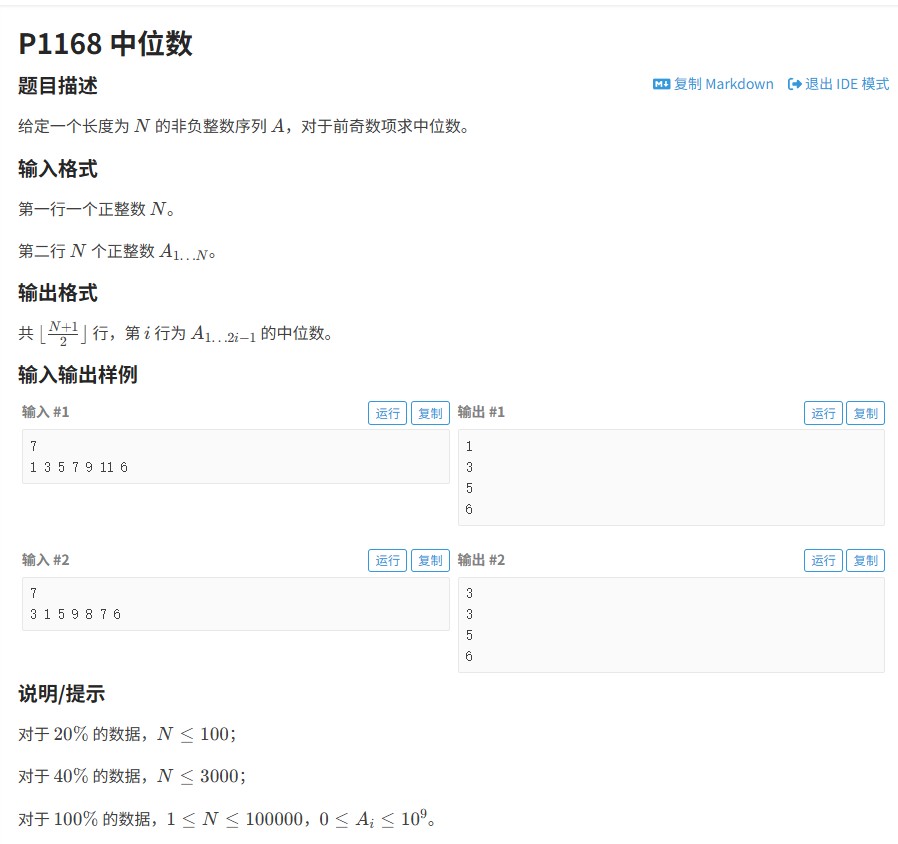
一、问题理解与算法思路 题目要求我们动态维护一个序列，并在每次读取奇数个数字时输出当前序列的中位数。这道题考察了两个核心算法点：堆数据结构的应用和中位数的高效计算。我们采用双堆法（一个大根堆和一个小根堆）来高效解决这个问题。

‌解题关键步骤‌：

使用大根堆存储较小的一半数 使用小根堆存储较大的一半数 保持两个堆的大小平衡 在奇数位置时输出大根堆的堆顶元素 二、完整代码实现（带详细注释）

#include <iostream>
#include <vector>
#include <queue>
using namespACe std;

int main() {
    ios::sync_with_stdio(false);  // 关闭同步，提高输入输出速度
    cin.tie(nullptr);             // 解除cin和cout的绑定

    int N;
    cin >> N;
    vector<int> A(N);  // 存储输入序列
    for (int i = 0; i < N; ++i) {
        cin >> A[i];    // 读取输入数据
    }

    // 大根堆存储较小的一半数
    priority_queue<int> max_heap;
    // 小根堆存储较大的一半数
    priority_queue<int, vector<int>, greater<int>> min_heap;

    for (int i = 0; i < N; ++i) {
        // 将新元素插入到合适的堆中
        if (max_heap.empty() || A[i] <= max_heap.top()) {
            max_heap.push(A[i]);  // 小于等于大根堆顶元素，放入大根堆
        } else {
            min_heap.push(A[i]);  // 否则放入小根堆
        }

        // 平衡两个堆的大小，保持max_heap比min_heap多0或1个元素
        if (max_heap.size() > min_heap.size() + 1) {
            min_heap.push(max_heap.top());  // 大根堆过大，移动元素到小根堆
            max_heap.pop();
        } else if (min_heap.size() > max_heap.size()) {
            max_heap.push(min_heap.top());  // 小根堆过大，移动元素到大根堆
            min_heap.pop();
        }

        // 输出前奇数项的中位数
        if ((i + 1) % 2 == 1) {
            cout << max_heap.top() << "\n";  // 中位数即大根堆顶元素
        }
    }

    return 0;
}

三、算法核心解析 ‌双堆结构‌：大根堆存储较小的一半数，小根堆存储较大的一半数 ‌元素插入策略‌：新元素根据与堆顶元素比较决定放入哪个堆 ‌堆平衡维护‌：保证大根堆最多比小根堆多一个元素 ‌中位数获取‌：奇数位置时，大根堆顶即为当前中位数 四、复杂度分析与优化 ‌时间复杂度‌：O(N log N)，每个元素插入堆操作耗时O(log N) ‌空间复杂度‌：O(N)，需要存储所有元素 ‌优化建议‌： 可以使用更高效的堆实现 对于特定数据分布可以考虑其他算法 五、常见问题解答 Q：为什么使用两个堆而不是排序？ A：排序的时间复杂度是O(N^2 log N)，而双堆法可以达到O(N log N)。

Q：如何处理偶数个元素的情况？ A：题目只要求输出奇数位置时的中位数，所以不需要处理偶数情况。

Q：算法是否可以扩展到求任意百分位数？ A：可以，通过调整两个堆的大小比例可以实现。

参考：洛谷P1168题终极解析：双堆法高效计算动态中位数 | 数据结构实战教程