一、逆序及逆序数
在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。也就是说,对于n个不同的元素,先规定各元素之间有一个标准次序(例如n个 不同的自然数,可规定从小到大为标准次序),于是在这n个元素的任一排列中,当某两个元素的实际先后次序与标准次序不同时,就说有1个逆序。一个排列中所有逆序总数叫做这个排列的逆序数。
如2431中,21,43,41,31是逆序,逆序数是4,计算过程如下:2逆序数1(1排其后)、4逆序数2(3、1排其后)、3逆序数1(1排其后)。
二、偶排列及奇排列
逆序数为偶数的排列称为偶排列;逆序数为奇数的排列称为奇排列。
如2431中,21,43,41,31是逆序,逆序数是4,为偶排列。
三、线性方程组
3.1、概念
线性方程组是各个方程关于未知量均为一次的方程组,下图为典型的线性方程组: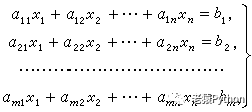
1)、式中x1,x2,…,xn代表未知量,αij(1≤i≤m,1≤j≤n)称为方程的系数,bi(1≤i≤m)称为常数项。系数和常数项都是任意的复数或某一个域的元素。
2)、当常数项b1,b2,…,bn都等于零时,则方程组称为齐次线性方程组。
上述方程组中各变量前面的系数构成的矩阵A:
称为方程的系数矩阵。在A中添加由常数项组成的列而得到一个m行n+1列矩阵: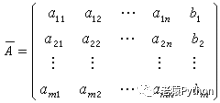
称为方程组的增广矩阵。
3.2、线性方程组的解
若x1=c1,x2=c2,…,xn=cn代入所给线性方程式的方程各式均成立,则称(c1,c2,…,cn)为该线性方程的一个解
若线性方程组的解c1,c2,…,cn不全为0,则称(c1,c2,…,cn)为线性方程的非零解
齐次线性方程组总有零解(0,0,…,0)
线性方程组有解,称为相容,否则称为不相容
两个方程组,若它们的未知量个数相同且解集相等,则称为同解方程组或等价方程组
线性方程组的方程个数低于未知量个数时,这个线性方程组没有唯一解,此时这个方程组有无穷多个解。想要确定地解出n个未知数,并且要求该结果唯一,则至少需要n个方程才行,但有n个方程不一定能确认唯一解,因为可能其中有些方程是无用的,例如将第一个方程和第二个方程相加构造的方程,或者直接在方程两端乘以系数构造的方程等。
3.3、线性方程组研究的主要问题
线性方程组主要讨论的问题是:
一个方程组有没有解,何时有解,即解的存在性
有解方程组解的个数,是否只有一个,即解的唯一性。
对有解方程组求解,如果存在多个解,能否把每一个解都找到,并能说明不同解之间的关系,这就是研究线性方程组解的结构。
四、n阶行列式
4.1、定义
按照一定的规则,由排成正方形的一组(n个)数(称为元素)之乘积形成的代数和,称为n阶行列式。
对于方阵: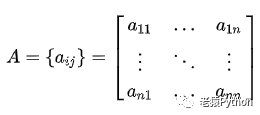
定义它的行列式为:
aij叫做第i行j列的数或元。
行列式的结果为一标量,这里 j1,j2,…,jn是1,2,…,n的一个排列(一共有n!个排列),因此n阶行列式是由n! 项组成,式中: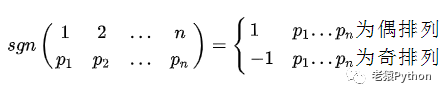
即每一项都按下列规则带有符号:当 j1,j2,…,jn是偶排列时带有正号,当 j1,j2,…,jn是奇排列时带有负号。
另外还有种方法确认行列式代数和计算公式中每项的符号:把项中的排列在行列式中的位置,每次互换两行或两列,把项中的所有元素移到行列式的对角位置,如果所需要互换的个数是偶数,则对应项的符号是正号,否则是负号。
案例1:2*2阶行列式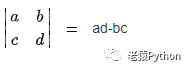
案例2:3*3阶行列式
4.2、行列式的主对角线和次对角线
行列式中从左上角到右下角的对角线称为主对角线,从右上角到左下角的对角线称为次对角线。
4.3、转置行列式
将行列式D的行变成列,列变成行,不改变它们间的前后顺序,则称该新行列式为转置行列式,即为D'。
4.4、对称行列式和反对称行列式
对于行列式:
如果对于任意i,j属于[1,n],aij=aji(ij、ji为下标),则称该行列式为对称行列式。
如果对于任意i,j属于[1,n],aij=-aji(ij、ji为下标),此时aii=0,则称该行列式为反对称行列式。
4.5、对角行列式
n阶对角行列式是指主对角线外的元素全0(称为主对角行列式)或次对角线外的元素全0(称为次对角行列式)的行列式。
主对角行列式的结果为主对角所有元的乘积,次对角行列式的结果的绝对值为次对角所有元的乘积,但其符号位由负一的n(n-1)/2次方来确认。即:

4.6、上下三角行列式
上(下)三角行列式是指主对角线以上(下)的元素全为0的行列式,上、下三角行列式的结果相等,都等于主对角线上元素的乘积。即:
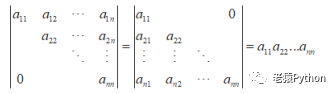
4.7、范德蒙行列式
形如:
的行列式称为范德蒙行列式。
若Dn 为n(n>=2)阶范德蒙行列式,则有:
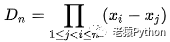
其中: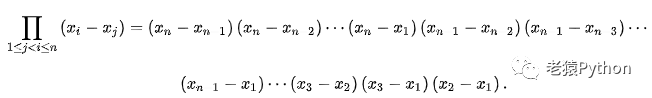
由范德蒙行列式的计算方法可以得出,该行列式为0的充要条件是至少x1,…,xn至少有两个相等。
4.8、n阶行列式的性质
性质1:行列互换,行列式不变。因此若两矩阵互为转置矩阵,则它们的行列式相等;
性质2:把行列式中某一行(列)的所有元素都乘以一个数K,等于用数K乘以行列式;
性质3 :如果行列式的某行(列)的各元素是两个元素之和,那么这个行列式等于两个行列式的和,即:如果A=[a1,…,ai,…,an],B=[a1,…,bi,…,an],C=[a1,…,ai+bi,…,an],则|C|=|A|+|B|;
性质4:如果行列式中有两行(列)相同,那么行列式为零。(所谓两行(列)相同就是说两行(列)的对应元素都相等);
性质5:如果行列式中两行(列)成比例,那么行列式为零;
性质6:把一行(列)的倍数加到另一行(列),行列式不变;
性质7:对换行列式中两行(列)的位置,行列式反号;
性质8:如果A=[a1,…,ai,…,an],且矢量组 a1,…,ai,…,an 线性相关,则|A|=0
五、子行列式及余子式
从行列式D中删除若干行与相同数目的列,所留下来的m行m列的部分仍然构成一个行列式,称为原行列式的m阶子式,常记作: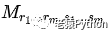
下标r1…rm表示保留下来的行,s1…sm表示保留下来的列,二者个数相同,但对应原行列式的行号和列号不一定相同,如行保留2、4、6等偶数行,而列保留奇数列,则二者完全不相同,但如果保留的下标满足对任意的i∈[1,m],ri = si,即保留的行号和列号完全相同,则称保留的子式为主子式。所删行与列的交点的元素也构成一个行列式,若将主子式记作 M ,则删除部分构成的行列式称为M的余子式,记作: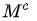
从另一个角度看, M也是原行列式关于其余子式的余子式。
将M的余子式 乘上系数: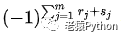
后得到的值记作:
称为与M对应的代数余子式。
特别地,在n阶行列式D中,把元素aij所在的第i行和第j列划去后,留下来的n-1阶行列式叫做元素aij的余子式,记作Mij,将余子式Mij再乘以-1i+j次方记为Aij,Aij叫做元素aij的代数余子式。即:Aij = (-1)i+jMij
aij在D中的余子式是它在D的转置行列式D'中的余子式的转置行列式。
六、行列式展开和拉普拉斯定理
6.1、定理1
n阶行列式D:
等于任一行中所有各元与它的代数余子式的乘积的和,即:
D = ai1*Ai1+ai2*Ai2+…+ain*Ain
这个定理通常说成把行列式按第i行展开,类似的,我们也可以将行列式按列展开,得到:
D = a1i*A1i+a2i*A2i+…+ani*Ani
6.2、定理2
n阶行列式的任意一行中各元与另一行中对应元的代数余子式乘积的和等于0,即:
aj1*Ai1+aj2*Ai2+…+ajn*Ain = 0 (i≠j)
同样地,行换成列同样成立,即:
a1j*A1i+a2j*A2i+…+anj*Ani = 0 (i≠j)
6.3、定理合并
把定理1和定理2合并,得到如下两个重要公式: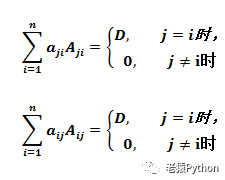
引入克朗耐克符号: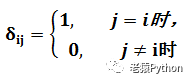
上面两个公式可以写成: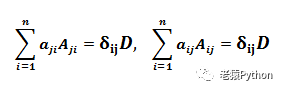
6.4、拉普拉斯定理
拉普拉斯定理是计算降阶行列式的一种方法。
定理:
在n阶行列式D=|aij| 中,任意取定k行(列),1≤k≤n,由这k行(列)的元素所构成的一切k阶子式与其代数余子式的乘积的和等于行列式D的值。此展式称为拉普拉斯展式。
该定理又称为行列式按某k个行(列)展开。
七、用行列式求解线性方程组
7.1、二元线性方程组求解
对于二院线性方程组: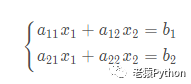
该线性方程组对应的增广矩阵为:
其对应的解为: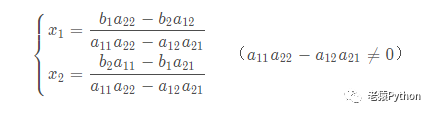
记: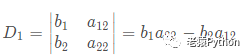
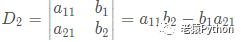
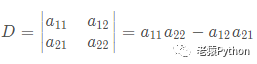
则上述线性方程组解记为: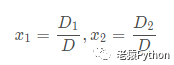
这样的表示方法,形状简单,容易记忆。
7.2、三元线性方程组求解
设三元线性方程组为: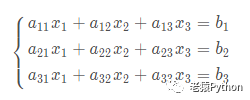
令: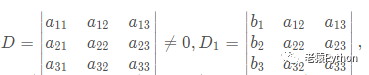
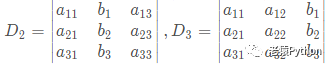
如果D ≠ 0则上述线性方程组有唯一解: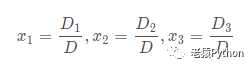
7.3、n元线性方程组求解
关于n元线性方程组求解,有如下重要定理。设线性方程组为: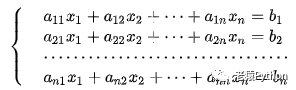
其系数行列式D:
若线性方程的系数矩阵对应的系数行列式 D≠0,则线性方程组有唯一解,其解为: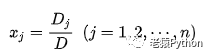
其中Dj是把D中第j列元素对应地换成常数项而其余各列保持不变所得到的行列式。
以上定理称为克莱姆定理或克莱姆法则。
根据克莱姆定理,如果方程组无解或者有两个不同的解,那么方程组的系数行列式必定等于零。
八、小结
本节介绍了与线性方程组求解相关的逆序及逆序数、偶排列及奇排列、行列式等相关的概念,介绍了使用行列式求解线性方程组的方法。使用克莱姆定理可以求解有唯一解的线性方程组的解,但当线性方程组变元较多时,这种方式运算量较大,求解一个N阶线性方程组要计算N+1个N阶行列式。另外当方程组系数的行列式等于零时,克莱姆法则失效。
参考资料:
1、百度百科n阶行列式相关知识介绍
2、百度百科克莱姆定理相关知识介绍
写博不易,敬请支持:
如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持!
更多人工智能数学基础的介绍请参考专栏《人工智能数学基础 》
本文转转自微信公众号老猿Python原创https://mp.weixin.qq.com/s/v3mSTzhdLaioi2S3mhhQxQ,如有侵权,请联系删除。













