红黑树,一种平衡二叉树,最为著名的应用就是C++ STL中的map,是有序集合最为理想的存储方式之一。除了二叉树所具有的属性之后,红黑树中每个节点多了一个“颜色”属性,可以是红色或者是黑色。一棵红黑树应该满足一下的性质:
- 每个节点是红色或者黑色的;
- 根节点是黑色的;
- 每个叶节点nil是黑色的(使用哨兵节点在删除调整时可以方便不少);
- 如果一个节点是红色的,那么它的两个子节点是黑色的;
- 对于每一个节点,到后代所有叶节点所经过的黑色节点数目相同。
根据定义,可以写出红黑树节点的数据结构:
struct Node {
enum Color { RED, BLACK };
Color _color;
Key _key;
Value _value;
Node *_parent, *_left, *_right;
Node(): _color(BLACK) {}
Node(const Key &key, const Value &value, Node *left, Node *right, Node *parent):
_key(key), _value(value), _color(RED), _left(left), _right(right), _parent(parent) {}
};本文省略了拷贝、析构、赋值等操作,完整源代码放在Gist上。
旋转
想要红黑树维持着平衡,就需要在插入元素和删除元素的过程中不断对结构进行调整。其中,最基础的操作就是左旋和右旋。
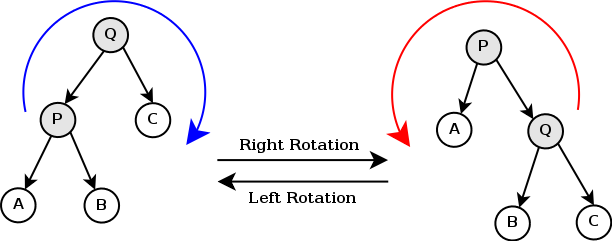
以左旋为例,操作可以分为三步:
- 将Q的左子节点变成P的右子节点;
- 将P变成Q的左子节点;
- 将Q变成当前子树的根节点。
void leftRotate(Node *x)
{
Node *y = x->_right;
// remove y->left to x->right
x->_right = y->_left;
if (x->_right != nil)
x->_right->_parent = x;
// remove y up
y->_parent = x->_parent;
if (x->_parent == nil)
root = y;
else if (x->_parent->_left == x)
x->_parent->_left = y;
else
x->_parent->_right = y;
// remove x down
x->_parent = y;
y->_left = x;
}插入
先污染,后治理。首选按照二叉树的插入方法先将节点插入二叉树,然后再对红黑树进行调整。
void insert(Node *nptr)
{
Node *it = root, *p = root;
// find insert position
while (it != nil) {
p = it;
if (nptr->_key < it->_key)
it = it->_left;
else if (nptr->_key > it->_key)
it = it->_right;
else {
// find target key-value
it->_value = nptr->_value;
return;
}
}
// insert
nptr->_parent = p;
if (p == nil)
root = nptr;
else if (nptr->_key < p->_key)
p->_left = nptr;
else
p->_right = nptr;
// fixup
insertFixup(nptr);
}在完成插入之后,将面临六种情况,由于存在左右对称的情况,实际上只需要考虑三种情况。
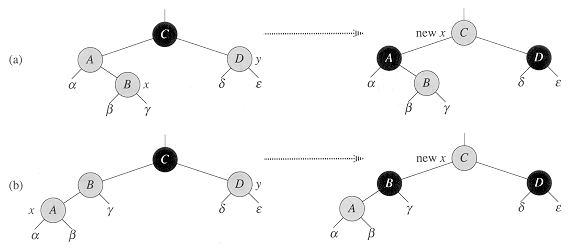
在情况1时,调整目标节点B的父节点和叔节点都是红节点,祖父节点为黑节点,我们需要将父节点和叔节点的颜色改成黑色,祖父节点设为红节点,并将调整目标设为祖父节点。
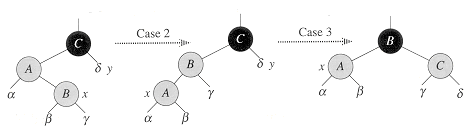
在情况2和情况3中,新插入节点的父节点为红节点,祖父节点为黑节点,并且叔节点为黑节点。首选需要把情况2转换成情况3,让B成为黑节点,A和C为B的红色子节点,并将调整目标设为A。往往在处理完这两种情况后,红黑树完成了调整。
由于NIL也算是黑色节点,所以还需要定义一个获取节点颜色的宏。
调整过程是自下而上的,一个插入的新节点的颜色是红色的,每次调整的目标是使每个子树保持红黑树的性质。对于情况2和3来说,调整结束后子树树根为黑色,对整体的性质不会造成影响。而在情况1中,子树树根为红色,对整体的性质造成了影响,需要继续调整,这就是循环条件的意义。
void insertFixup(Node *ptr)
{
while (ptr->_parent->_color == Node::RED) {
if (ptr->_parent == ptr->_parent->_parent->_left) {
Node *y = ptr->_parent->_parent->_right;
// case 1
if (y->_color == Node::RED) {
ptr->_parent->_color = Node::BLACK;
y->_color = Node::BLACK;
ptr->_parent->_parent->_color = Node::RED;
ptr = ptr->_parent->_parent;
} else {
// case 2: switch case 2 to case 3
if (ptr == ptr->_parent->_right) {
ptr = ptr->_parent;
leftRotate(ptr);
}
// case 3
ptr->_parent->_color = Node::BLACK;
ptr->_parent->_parent->_color = Node::RED;
rightRotate(ptr->_parent->_parent);
}
} else {
// with 'left' and 'right' exchanged
Node *y = ptr->_parent->_parent->_left;
if (y->_color == Node::RED) {
ptr->_parent->_color = Node::BLACK;
y->_color = Node::BLACK;
ptr->_parent->_parent->_color = Node::RED;
ptr = ptr->_parent->_parent;
} else {
if (ptr == ptr->_parent->_left) {
ptr = ptr->_parent;
rightRotate(ptr);
}
ptr->_parent->_color = Node::BLACK;
ptr->_parent->_parent->_color = Node::RED;
leftRotate(ptr->_parent->_parent);
}
}
}
root->_color = Node::BLACK;
}删除
删除的过程比插入过程复杂很多。与二叉树一样,我们需要一个替换操作,将子树u替换成子树v。
void transplant(shared_ptr<Node> u, shared_ptr<Node> v)
{
if (u->_parent == nil)
root = v;
else if (u == u->_parent->_left)
u->_parent->_left = v;
else
u->_parent->_right = v;
v->_parent = u->_parent;
}删除的过程和二叉树类似,多了一些处理哨兵、记录颜色的过程。
void remove(Node *ptr)
{
Node *y = ptr, *x;
int y_original_color = y->_color;
if (y->_left == nil) {
x = ptr->_right;
transplant(ptr, ptr->_right);
} else if (y->_right == nil) {
x = ptr->_left;
transplant(ptr, ptr->_left);
} else {
y = min(ptr->_right);
y_original_color = y->_color;
x = y->_right;
if (y->_parent == ptr)
x->_parent = y; // change nil->_parent
else {
transplant(y, y->_right);
y->_right = ptr->_right;
y->_right->_parent = y;
}
transplant(ptr, y);
y->_left = ptr->_left;
y->_left->_parent = y;
y->_color = ptr->_color;
}
if (y_original_color == Node::BLACK)
deleteFixup(x);
}首先考虑一下删除节点的时候,我们对红黑树造成了什么样的影响。如果删除一个红色节点,那么红黑树的性质并不会收到任何影响;如果删除的是一个黑色节点,那么意味着黑高相等的性质将不复存在,删除一个黑色节点。那么和插入调整的思路类似,每次调整的目标是保持子树内的性质。
调整过程需要分左右对称的四种情况:
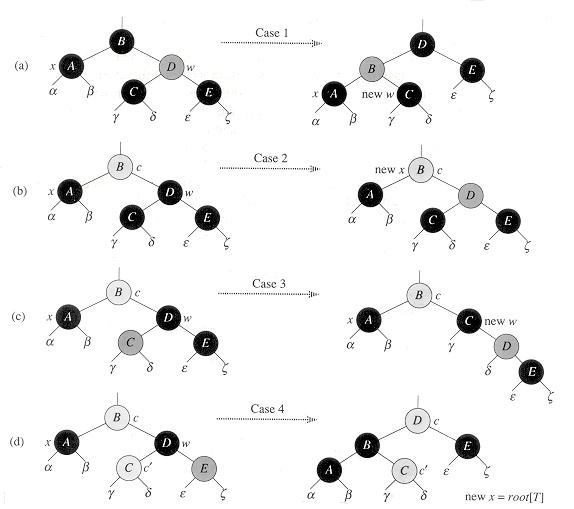
- 情况1:有一个红色的兄弟节点,通过旋转和颜色调换,使红色节点到调整目标节点一侧来,变成情况2、3、4中的一种;
- 情况2:兄弟节点的两个子节点全为黑,于是把兄弟节点设为红节点,这样一来,子树中的黑高是相等了,但是删除的黑节点并没有被弥补,还需要继续往上调整;
- 情况3:兄弟节点左红右黑,这个时候需要把红色节点调整到叔节点的右侧,变成情况4;
- 情况4:兄弟节点右节点为红,这个时候需要把红节点调整到调整目标节点一侧来,用这个红色节点弥补删除的黑色节点。调整结束后,子树满足红黑树性质,结束调整过程。
而对于循环条件。应该怎么理解呢?如果调整过程到了根节点,那么就不存在某子树内黑高缺一的情况,可以结束循环。如果遇到了红节点,那么把这个红节点变成黑节点就可以解决黑高不等的情况。
void removeFixup(Node *ptr)
{
while (ptr != root && ptr->_color == Node::BLACK) {
if (ptr == ptr->_parent->_left) {
Node *w = ptr->_parent->_right;
// case 1
if (w->_color == Node::RED) {
w->_color = Node::BLACK;
ptr->_parent->_color = Node::RED;
leftRotate(ptr->_parent);
w = ptr->_parent->_right;
}
// case 2
if (w->_left->_color == Node::BLACK && w->_right->_color == Node::BLACK) {
w->_color = Node::RED;
ptr = ptr->_parent;
} else {
// case 3
if (w->_right->_color == Node::BLACK) {
w->_left->_color = Node::BLACK;
w->_color = Node::RED;
rightRotate(w);
w = ptr->_parent->_right;
}
// case 4
w->_color = ptr->_parent->_color;
ptr->_parent->_color = Node::BLACK;
w->_right->_color = Node::BLACK;
leftRotate(ptr->_parent);
ptr = root;
}
} else {
// with 'left' and 'right' exchanged
Node *w = ptr->_parent->_left;
if (w->_color == Node::RED) {
w->_color = ptr->_parent->_color;
ptr->_parent->_color = Node::RED;
rightRotate(ptr->_parent);
w = ptr->_parent->_left;
}
if (w->_left->_color == Node::BLACK && w->_right->_color == Node::BLACK) {
w->_color = Node::RED;
ptr = ptr->_parent;
} else {
if (w->_left->_color == Node::BLACK) {
w->_color = Node::RED;
w->_right->_color = Node::BLACK;
leftRotate(w);
w = ptr->_parent->_left;
}
w->_color = ptr->_parent->_color;
w->_left->_color = Node::BLACK;
ptr->_parent->_color = Node::BLACK;
rightRotate(ptr->_parent);
ptr = root;
}
}
}
ptr->_color = Node::BLACK;
}查找
节点颜色对于查找过程没有意义,红黑树查找过程和二叉树是一样的。