B树广泛应用于各种文件系统，文件系统中，数据都是按照数据块来进行读取操作。结合二叉树的优点和文件系统的特点，于是就有了B树：

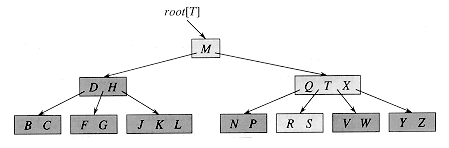
B树当中每个节点存储着一组数据，数据的数量由B树的度来决定。

B树中的节点包含以下内容：

• 大小(size)：用来记录当前节点中元素的个数；

• 关键字(key)：B树是有序集合，关键字是可比的，用于在集合中定位卫星数据；

• 是否为叶子节点(leaf)：节点类型可以分为内部节点和叶子节点。

• 孩子节点(children)：如果当前节点是一个内部节点的话，那么就有更加底层的孩子节点。如果是叶子节点。那就没有孩子节点。孩子节点的数量总是比数据的数量多一个。

对于一个度数为N的B树，需要保持以下性质：

• 一个节点中的数据量不小于N-1并且不大于2N-1，一个例外就是根节点可以包含小于N-1数量的数据;

• 所有的叶子节点高度相等；

• 在节点中，所有的数据关键字保持递增关系(key[0] < ... < key[size-1])；

• 对于一个孩子节点children[i]，children[i]子树中所有关键大于key[i-1]并且小于key[i](key[-1]=-∞，key[size]=+∞)。

度数小于2的B树是没有意义的，因此度数最小的取值为2。完整的B树实现见Gist。

节点定义

B树中不存在循环引用，因此可以大胆使用shared_ptr来代替原生指针，简化析构操作。B树的拷贝可以通过递归进行，因此数据结构地拷贝也就简单了很多。

struct Node
{
    bool _leaf;
    int _size;
    vector<Key> _keys = vector<Key>(2*N-1);
    vector<Value> _values = vector<Value>(2*N-1);
    vector<shared_ptr<Node>> _children = vector<shared_ptr<Node>>(2*N);
    Node() = default;
    Node(const Node &node): _leaf(node._leaf), _size(node._size), _keys(node._keys), _values(node._values)
    {
        if (!_leaf)
            for (int i = 0; i <= _size; i++)
                _children[i] = std::make_shared<Node>(*node._children[i]);
    }
};

创建

创建一个空地叶子结点，作为根节点。

BTree()
{
    root = std::make_shared<Node>();
    root->_leaf = true;
    root->_size = 0;
}

查找

如果在当前节点找到关键字，返回卫星数据指针。如果没有找到关键字，那么需要检查当前节点是否为叶节点，如果是叶节点，那么说明关键字不存在，返回指针，如果是内部节点，那么在子树中查找关键字。

Value* find(shared_ptr<Node> node, Key key)
{
    // search key in node
    int i = 0;
    while (i < node->_size && key > node->_keys[i])
        i++;
    if (i < node->_size && key == node->_keys[i])
        return &node->_values[i];
    else if (node->_leaf)
        return nullptr;
    else return find(node->_children[i], key);
}

分裂

当一个节点数据量到达2N-1时后，如果想要继续插入，就需要对节点进行分裂。把孩子节点中间元素提升到父节点中，然后产生两个新的孩子节点分别插入中间元素两侧。

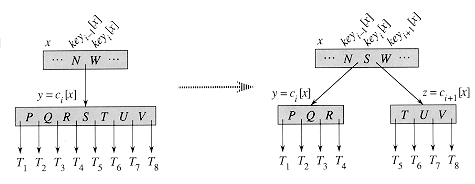
// split a full node (child.size == 2*N-1)
void split(shared_ptr<Node> parent, int i, shared_ptr<Node> child)
{
    shared_ptr<Node> nchild = std::make_shared<Node>();
    nchild->_leaf = child->_leaf;
    nchild->_size = child->_size = N-1;
    // move k-v
    for (int j = 0; j < N-1; j++) {
        nchild->_keys[j] = child->_keys[j + N];
        nchild->_values[j] = child->_values[j + N];
    }
    // move children
    if (!child->_leaf)
        for (int j = 0; j < N; j++)
            nchild->_children[j] = child->_children[j + N];
    // move child->key[N-1] up
    for (int j = parent->_size; j > i; j--) {
        parent->_keys[j] = parent->_keys[j-1];
        parent->_values[j] = parent->_values[j-1];
        parent->_children[j+1] = parent->_children[j];
    }
    parent->_keys[i] = child->_keys[N-1];
    parent->_values[i] = child->_values[N-1];
    parent->_children[i+1] = nchild;
    parent->_size++;
}

合并

合并操作是分裂操作的逆向过程。

// combine children[i] and children[i+1]
void combine(shared_ptr<Node> parent, int i)
{
    shared_ptr<Node> prev = parent->_children[i];
    shared_ptr<Node> next = parent->_children[i+1];
    // move parent->key[i] down
    prev->_keys[prev->_size] = parent->_keys[i];
    prev->_values[prev->_size] = parent->_values[i];
    prev->_size++;
    // move k-v from next to prev
    for (int j = 0; j < next->_size; j++) {
        prev->_keys[j + prev->_size] = next->_keys[j];
        prev->_values[j + prev->_size] = next->_values[j];
    }
    if (!prev->_leaf)
        for (int j = 0; j <= next->_size; j++)
            prev->_children[j + prev->_size] = next->_children[j];
    prev->_size += next->_size;
    // remove parent->key[i]
    parent->_size--;
    for (int j = i; j < parent->_size; j++) {
        parent->_keys[j] = parent->_keys[j+1];
        parent->_values[j] = parent->_values[j+1];
        parent->_children[j+1] = parent->_children[j+2];
    }
}

插入

当根节点满了，需要创建一个新的根节点，然后将旧的根节点分裂，成为新的根节点的子节点。

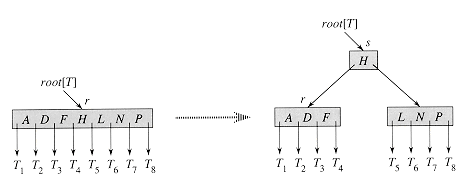
// insert k-v in root node
void insert(Key key, Value value)
{
    shared_ptr<Node> ptr = root;
    if (ptr->_size == 2*N-1) {    // split root node
        root = std::make_shared<Node>();
        root->_leaf = false;
        root->_size = 0;
        root->_children[0] = ptr;
        split(root, 0, ptr);
        insert(root, key, value);
    } else insert(root, key, value);
}

• 插入叶节点：直接插入即可。

• 插入内部节点：首先，找到新关键字所在的子节点，如果子节点满，进行分裂。然后插入到合适的子节点中。

void insert(shared_ptr<Node> node, Key key, Value value)
{
    // find insert position
    int i = 0;
    while (i < node->_size && key > node->_keys[i])
        i++;
    if (node->_leaf) {    // insert k-v in a leaf
        for (int j = node->_size; j > i; j--) {
            node->_keys[j] = node->_keys[j-1];
            node->_values[j] = node->_values[j-1];
        }
        node->_keys[i] = key;
        node->_values[i] = value;
        node->_size++;
    } else {            // insert k-v in subnode
        shared_ptr<Node> ptr = node->_children[i];
        if (ptr->_size == 2*N-1) {
            split(node, i, ptr);
            if (key > node->_keys[i])
                i++;
        }
        insert(node->_children[i], key, value);
    }
}

删除

和插入操作一样，删除操作也是自顶向下对B树进行调整，必须保证要删除的关键字位于B树中，否则会产生意想不到的后果，对于删除操作，处理方式如下：

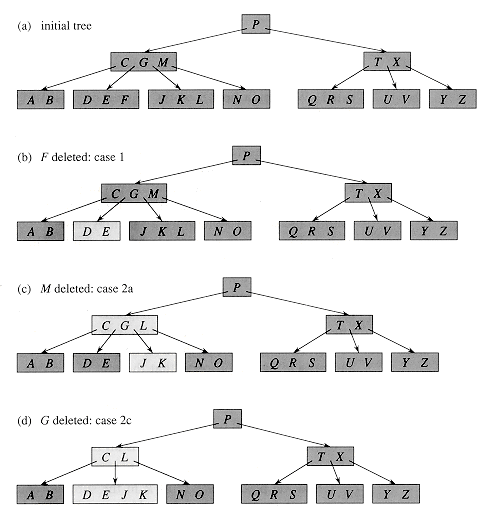
• 情况1，当前节点是叶子节点，找到关键字：直接删除关键字即可。

• 情况2，当前节点是内部节点，找到关键字key[i]：

  • 情况2a，如果关键字的左孩节点children[i]->size>=N：用children[i]中的最大元素（关键字的前驱）代替关键字，然后在children[i]中删除最大元素。

  • 情况2b，如果关键字的右孩节点children[i+1]->size>=N：用children[i+1]中的最小元素（关键字的后继）代替关键字，然后在children[i+1]中删除最小元素

  • 情况2c，如果关键字的左右两个子节点都小于N-1：这时可以合并两个子节点，于是关键字key[i]落入新合并成的节点中，接着在新的节点中删除关键字。

• 情况3，当前节点是内部节点，找到关键字所在的子树children[i]：如果children[i]->size<N，那么还需要进行一些调整之后再删除。

  • 情况3a，如果children[i]的某个相邻兄弟节点children[x]->size>=N：通过移动操作，使得children[x]元素数量减一，children[i]元素数量加一。

  • 情况3b，如果children[i]的所有相邻兄弟节点children[x]->size < N：将children[i]和任意一个children[x]合并。（到底和左边的合并好还是右边的好，好纠结~）

// remove key from node, key must be in node
void remove(shared_ptr<Node> node, Key key)
{
    // find delete position
    int i = 0;
    while (i < node->_size && key > node->_keys[i])
        i++;
    if (node->_leaf) {                                        // case 1: remove k-v from leaf
        node->_size--;
        for (int j = i; j < node->_size; j++) {
            node->_keys[j] = node->_keys[j+1];
            node->_values[j] = node->_values[j+1];
        }
    } else if (i < node->_size && key == node->_keys[i]) {    // case 2: find key in internal node
        shared_ptr<Node> prevChild = node->_children[i];
        shared_ptr<Node> nextChild = node->_children[i+1];
        if (prevChild->_size >= N) {                        // case 2a: move precursor to the position of key
            shared_ptr<Node> maxNode = max(prevChild);
            node->_keys[i] = maxNode->_keys[maxNode->_size-1];
            node->_values[i] = maxNode->_values[maxNode->_size-1];
            remove(prevChild, maxNode->_keys[maxNode->_size-1]);
        } else if (nextChild->_size >= N) {                    // case 2b: move successor to the position of key
            shared_ptr<Node> minNode = min(nextChild);
            node->_keys[i] = minNode->_keys[0];
            node->_values[i] = minNode->_values[0];
            remove(nextChild, minNode->_keys[0]);
        } else {                                            // case 2c: combine previous child and next child
            combine(node, i);
            remove(node->_children[i], key);
        }
    } else {                                                        // case 3
        shared_ptr<Node> subNode = node->_children[i];
        if (subNode->_size < N) {
            shared_ptr<Node> prevBrother, nextBrother;
            if (i > 0)                prevBrother = node->_children[i-1];
            if (i < node->_size)    nextBrother = node->_children[i+1];
            if (prevBrother && prevBrother->_size >= N) {            // case 3a
                // remove node->key[i] into subNode
                for (int j = subNode->_size; j > 0; j--) {
                    subNode->_keys[j] = subNode->_keys[j-1];
                    subNode->_values[j] = subNode->_values[j-1];
                }
                if (!subNode->_leaf)
                    for (int j = subNode->_size; j >= 0; j--)
                        subNode->_children[j+1] = subNode->_children[j];
                subNode->_keys[0] = node->_keys[i-1];
                subNode->_values[0] = node->_values[i-1];
                subNode->_children[0] = prevBrother->_children[prevBrother->_size];
                subNode->_size++;
                // remove prevBrother->key[prevBrother->size-1] into node
                node->_keys[i-1] = prevBrother->_keys[prevBrother->_size-1];
                node->_values[i-1] = prevBrother->_values[prevBrother->_size-1];
                prevBrother->_size--;
            } else if (nextBrother && nextBrother->_size >= N) {    // case 3a    
                // remove node->key[i] into subNode
                subNode->_keys[subNode->_size] = node->_keys[i];
                subNode->_values[subNode->_size] = node->_values[i];
                subNode->_children[subNode->_size+1] = nextBrother->_children[0];
                subNode->_size++;
                // remove nextBrother->key[0] into node
                node->_keys[i] = nextBrother->_keys[0];
                node->_values[i] = nextBrother->_values[0];
                nextBrother->_size--;
                for (int j = 0; j < nextBrother->_size; j++) {
                    nextBrother->_keys[j] = nextBrother->_keys[j+1];
                    nextBrother->_values[j] = nextBrother->_values[j+1];
                }
                if (!nextBrother->_leaf)
                    for (int j = 0; j <= nextBrother->_size; j++)
                        nextBrother->_children[j] = nextBrother->_children[j+1];
            } else if (nextBrother) {    // case 3b: combine child[i] and child[i+1]
                combine(node, i);
            } else {                    // case 3b: combine child[i-1] and child[i]
                i--;
                combine(node, i);
            }
        }
        remove(node->_children[i], key);
    }
}

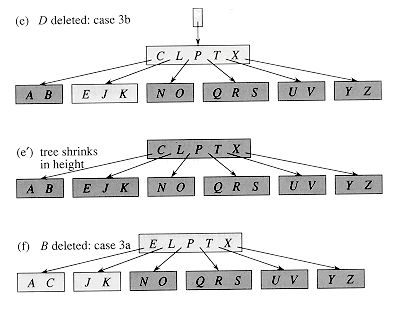
随着删除不断进行，会出现根节点变为空的情况，这时候需要把空的根节点删除。如果B树中的元素被全部删除，那么需要重新创建一个根节点。由于删除过程会改变B树结构，需要再删除前检查关键字是否存在。

void remove(const Key &key)
{
    if (find(root, key))
        remove(root, key);
    if (root->_size == 0)
        root = root->_children[0];
    if (root == nullptr) {
        root = std::make_shared<Node>();
        root->_leaf = true;
        root->_size = 0;
    }
}