基于01背包问题的动态规划算法 - HelloWorld开发者社区

初步认识动态规划

动态规划算法是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。

我们可以简单地将动态规划与贪心算法进行对比以方便理解(如果不理解就跳了吧)：

通过在每个局部的问题中都求出最优解，从而得到全局的最优解：对于贪心算法而言，通过一系列局部最优的选择得到所求问题的整体最优解。其中选择的贪心策略必须具备无后效性(某个状态以前的过程不会影响以后的状态，只与当前状态有关)。当前最优解从子问题最优解即可得出，即由上一步的最优解推导下一步的最优解，而上一部之前的最优解则不作保留。并且，每一步的最优解一定包含上一步的最优解。

通过求出的局部最优解来推导全局最优解: 对于动态规划算法而言，全局最优解中一定包含某个局部最优解，但不一定包含前一个局部最优解，因此需要记录之前的所有最优解。将待求解的问题分解为若干个子问题（阶段），通过求解前一子问题(阶段)的解为后一子问题的求解提供了有用的信息。在求解任一子问题时，通过决策保留那些有可能达到最优的局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

与动态规划有关的理论知识：

最优性原理
无后效性
有重叠子问题(非必要性质)

在上一篇文章中，我们已经分析过01背包问题分治解法的思路。并且提到了动态规划算法的基本思想与分治法类似，都是把原问题分解成子问题进行求解。而不同之处，也是动态规划的核心之处，在于动态规划自底向上地求出子问题中的局部最优解并记录下来，从而推导出全局最优解(即原问题答案)。

现在，我们定义一个数组二维values记下子问题中计算过的v_total值。当n=0或c=0，即可选物品数量或背包容量为0时，结果直接返回0；当在计算一个子问题时，先查看数组中是否已经计算过，若是，则直接返回结果，否则对该子问题进行计算。

下面给出关键代码：

int V_total(int i, int j)
{
    if (values[i][j])
        return values[i][j]; //如果结果已经计算过，直接返回
    int value = 0;
    if (i == 0 || j == 0) //当可选物品数量或背包容量为0时，返回0
        value = 0;
    else if (j < w[i]) //背包容量不足
        value = V_total(i - 1, j);
    else
    {
        value = max(V_total(i - 1, j), V_total(i - 1, j - w[i]) + v[i]);
        values[i][j] = value;
    }
    return value;
}

基于01背包问题的动态规划算法

（提交仍TLE）

动态规划中的最优决策表

以该图为例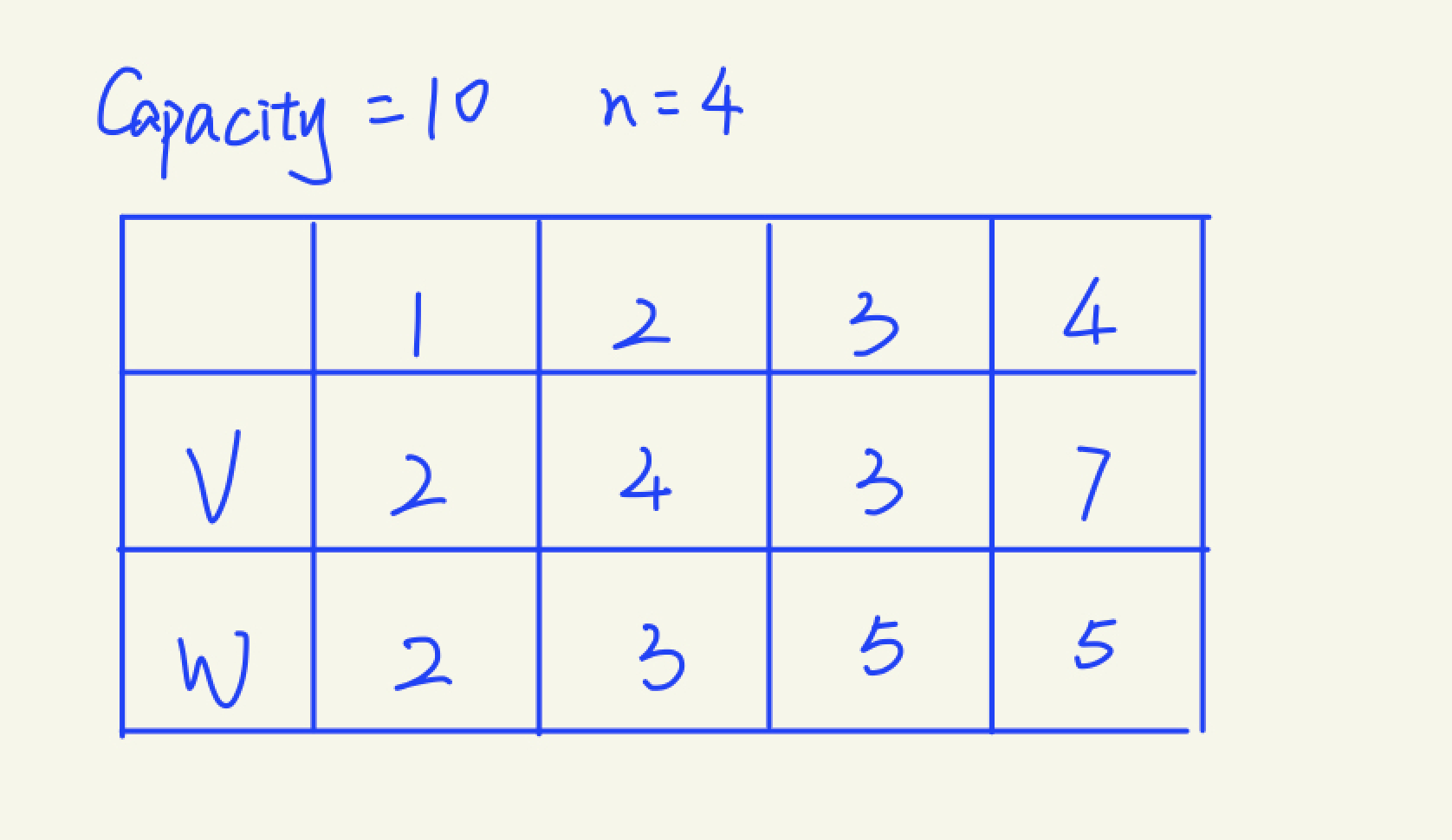基于01背包问题的动态规划算法 )

在下图的表格中，每一个格子都代表着一个子问题，我们最终的问题是求最右下角的格子的值*（认真想想为什么?)*，也就是i=4,j=10时的值。这里，如果可选物品数量i为0，或者剩余容量j为0，那么最大价值自然也是0。

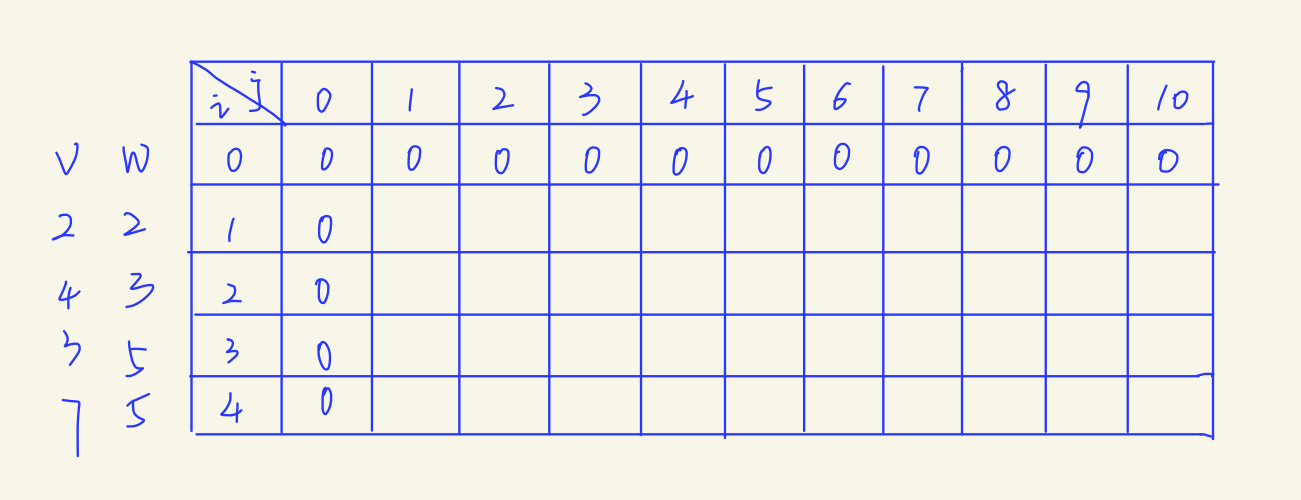基于01背包问题的动态规划算法 )

现在我们开始一行行填表

当i=1时，即只有珠宝1可供选择，那么如果容量足够的话，最大价值自然就是珠宝1的价值了。

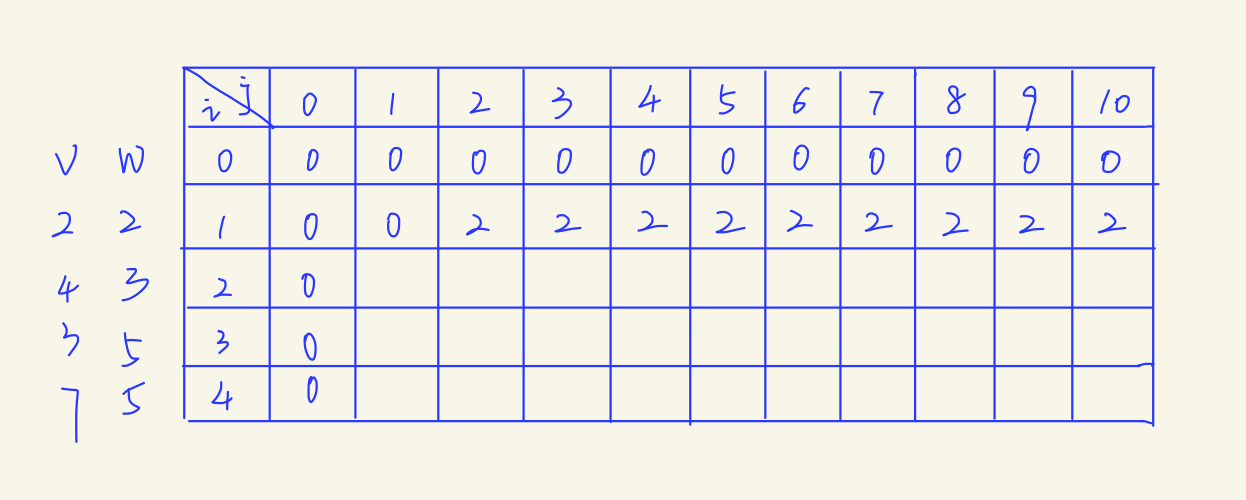基于01背包问题的动态规划算法 )

当i=2时，有两个物品可供选择，此时应用上面的递推关系式进行判断即可。这里以i=2,j=3为例进行分析：

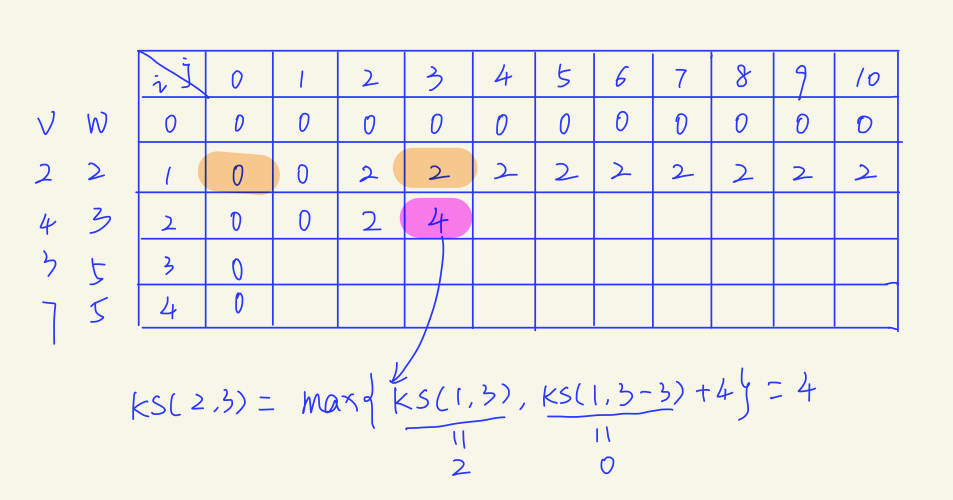基于01背包问题的动态规划算法 )

剩下的格子使用相同的方法进行填充即可：

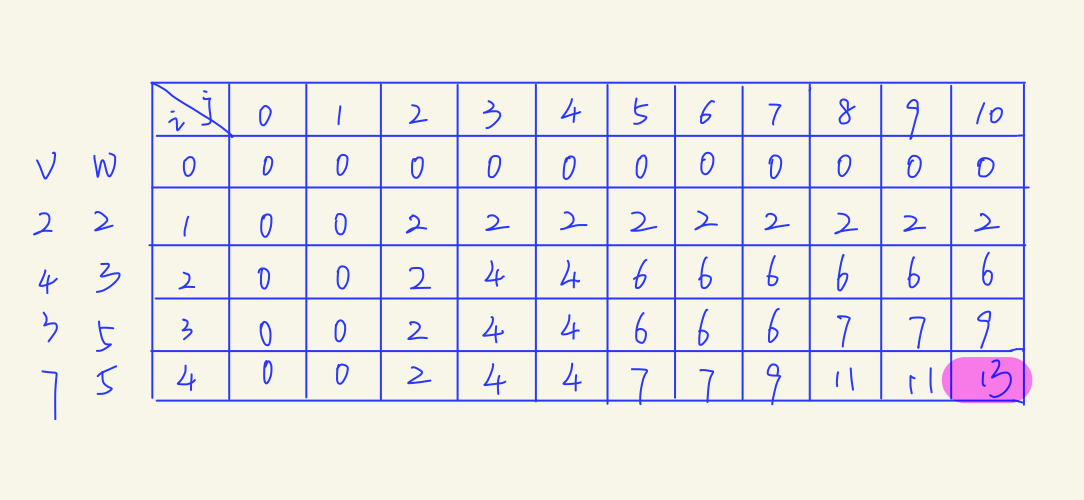基于01背包问题的动态规划算法 )

最后，在表格中最右下角的格子得到了我们最终要求的最大值13。通过填表，我们再也不用递归求解啦。

将填表过程转为代码：

for (int i = 1; i <= n; i++) //开始填表，表中初始值为0
    for (int j = 1; j <= c; j++)
        if (j < w[i]) //背包容量不够
            values[i][j] = values[i - 1][j];
        else //将价值最优的填入表中
            values[i][j] = max(values[i - 1][j], values[i - 1][j - w[i]] + v[i]);
cout << values[i][j];

基于01背包问题的动态规划算法

(终于我们将时间复杂度优化为填表时间O(nc)，然而空间复杂度也是O(nc),于是不可避免地MLE了...看来还不能收工，让我们继续优化，坚持住！)

最终版动态规划

现在，让我们回顾下最初的递推关系

基于01背包问题的动态规划算法 )

可以发现，*每次求解 V_total(i,j)只与V_total(i-1,tj) {1<=tj<=j} 有关。*也就是说，如果我们知道了V_total(i-1,1...j)就肯定能求出V_total(i,j)，为了更直观的理解，再画一张图：

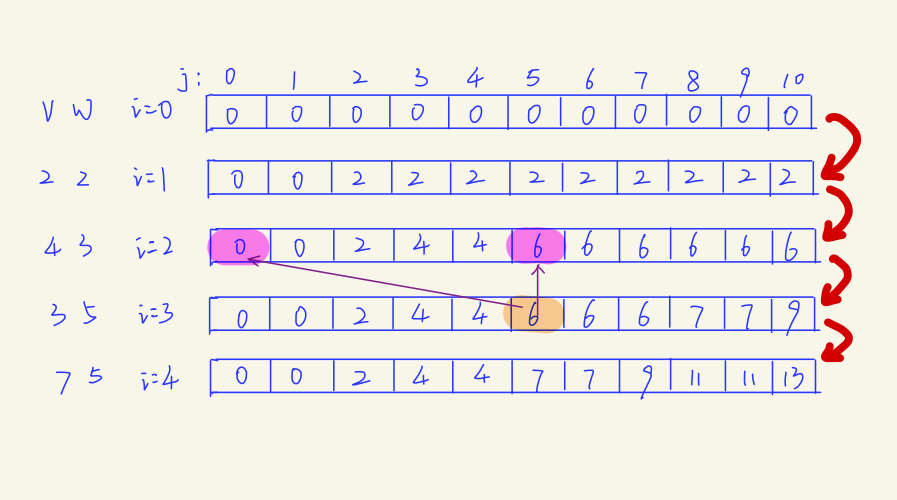基于01背包问题的动态规划算法 )

在这张决策表中，下一层只需要根据上一层的结果即可推出答案。比方说，看表中i=3，j=5，在求这个子问题的最优解时，根据上述推导公式，V_total(3,5) = max{KS(2,5),KS(2,0) + 3} = max{6,3} = 6;如果我们得到了i=2时所有子问题的解，那么就很容易求出i=3时所有子问题的解。

因此可以将求解空间进行优化，将二维数组压缩成一维数组。根据上述的分析，我们有如下状态转移方程：

V_total(j) = max{V_total(j),V_total(j - wi) + vi}

(如果不理解，尝试通过将状态转移方程与上面的递推公式对比。每次求解 V_total(i,j)只与V_total(i-1,j or j-wi) 有关)

这里V_total(j - wi)就相当于原来的V_total(i-1, j - wi)。

注意：

我们从i=2推算i=3的子问题的解时，一维数组中存放的是{0,0,2,4,4,6,6,6,6,6,6}，这是i=2时所有子问题的解。如果我们从前往后推算i=3时的解——比如，我们计算V_total(0) = 0，V_total(1) =V_total(1) = 0 (因为j=1时，装不下第三个物品，第三个物品重量为5)，V_total(2) = 2,V_total(3) = 4,V_total(4) = 4,V_total(5)=max{V_total(5),V_total(5-5) + 3}= 6.....

V_total(8) = max{V_total(8),V_total(8 - 5) + 3} = 7。在这里计算V_total(8)的时候，我们就把原来V_total(8)的内容修改掉了。这样，我们后续计算就无法找到这个位置的原值，也就是上一轮循环中计算出来的值了。

由于V_total(j)是由它前面的V_total(tj){1<=tj<=j}推导出来的，所以在第二轮循环扫描的时候应该由后往前进行计算，因为如果由前往后推导的话，前一次循环保存下来的值可能会被修改，从而造成错误。

最后，附上AC代码：

#include <bits/stdc++.h>
using namespace std;
int n, c, d;
int v[10005], w[10005], dp[10005];
int main()
{

    cin >> n >> c >> d;
    for (int i = 1; i <= n; i++)
        cin >> w[i] >> v[i];
    for (int i = 1; i <= n; i++) //遍历每个物品，开始填表
        for (int j = c; j >= w[i];j--) //从后往前，倒序推导
            dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
    cout << d + dp[c]; //返回最右下角的格子的值即问题的解
}

基于01背包问题的动态规划算法

终于大功告成！

总结：

动态规划问题，大致可以通过以下四部进行解决。

1.划分状态，即划分子问题(核心思想）

2.状态表示，即如何让计算机理解子问题。(用二维数组表示最优决策表中每个子问题的解）

3.状态转移，即父问题是如何由子问题推导出来的(核心步骤，通过递推关系、问题的阶段和每个阶段的状态推导状态转移方程)。

4.确定边界，确定初始状态是什么、最小的子问题以及最终状态。(最后，开始写代码吧！)

在01背包问题中，每件物品最多选择一次，如果可以多次选择同一个物品时，又该怎么办呢？请看下一篇文章：完全背包问题

本文转自 https://blog.csdn.net/guanguandaren/article/details/107948287，如有侵权，请联系删除。