初步了解01背包问题（分治篇） - HelloWorld开发者社区

问题描述

Coda非常喜欢玩“NewWorld Online”，受到某部动画的影响，他决定创建名为“梅普露”的角色，并把所有技能点都加到防御力上。Coda发现了一个包含了n行数据的列表，表上每行有一组数据，包含两个整数ai 和bi，决定了第i 次点技能时消耗ai 点技能点，提升bi 点属性值。

Coda在加点时可以从列表中选择喜欢的一组数据作为加点时的消耗和提升，但是每组数据使用过一次就不能再次使用了。

Coda现在拥有p个技能点，初始防御力为d，请问如果Coda把这些技能点全拿来加防御力，最高能到达多少防御力？

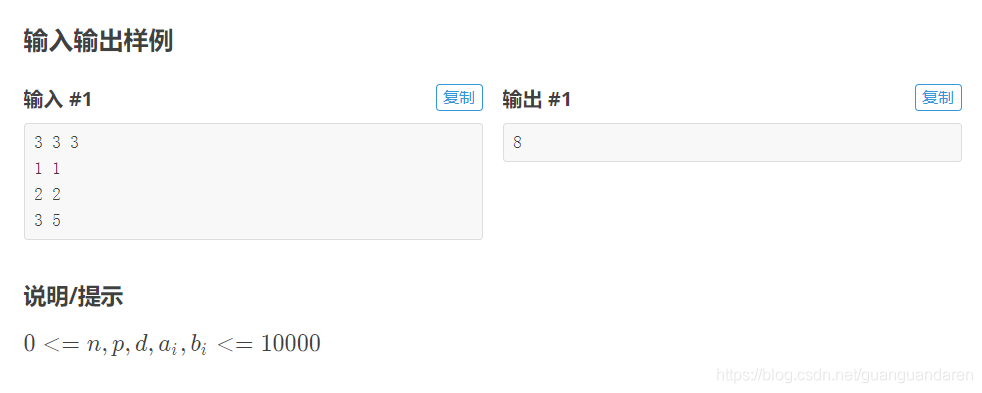
输入格式

第一行包含3个整数: n，p，d，分别表示列表中数据组数、拥有的技能点数和初始防御力。接下来n行，每行包含2个整数ai，bi，分别表示列表中各组数据，ai 是加点时技能点的消耗，bi 是加点时防御力的提升。

输出格式

一行，包含一个整数，最大可以达到的防御力。

)

（如果想要直接看动态规划部分，请直接点击动态规划篇前往下一篇文章）

这是一个经典的【01背包】问题:

有N个物品，它们有各自的体积wi 和价值vi，现有给定容量C的背包，如何让背包里装入的物品具有最大的价值总和？

贪心的尝试

在上一篇文章中，我们提到一种直接选择当前最优解的贪心算法。现在，让我们开启贪婪模式——既要装得多，又要价值高，那么就选性价比最高的好了——按照物品单价从大到小来装。 这可行吗？

在重量相同的情况下，我们总会选择对价值贡献最大的物品。然而，我们并不能确定这个贪心策略能否把背包装满。

我们只是按照了单价更高的策略依次对物品作选择。但物品不可分割。因此这个贪心策略只是解决了部分背包问题，在这里不能成立。我们很容易能够给出反例，当所有的物品单价相同，又或者：

N=3,C=30

物品：A B C

重量：20 15 15

价值：30 20 20

让我们理解一下贪心算法的适用情况：

因为贪心策略是由上一步的最优解推导下一步的最优解，而上一部之前的最优解则不作保留，并且，每一步的最优解一定包含上一步的最优解。在贪心算法中，作出的每步贪心决策都无法改变。

所谓贪心选择性质，是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。换句话说，当考虑做何种选择的时候，我们只考虑对当前问题最佳的选择而不考虑子问题的结果。这是贪心算法可行的第一个基本要素。贪心算法以迭代的方式作出相继的贪心选择，每作一次贪心选择就将所求问题简化为规模更小的子问题。

对于一个具体问题，要确定它是否具有贪心选择性质，每一步的最优解一定包含上一步的最优解。则必须证明每一步所作的贪心选择最终导致问题的整体最优解。

这可咋办呢?贪心用不了，dp又不会，只能用暴力天天TLE才能水水题这样子。

基于01背包的迭代算法

01背包问题的分析

01背包问题，顾名思义，是0/1的规划问题。由于物品不可分割且只能拿一次，于是对于每个物品只有两个选择：盘它或者不盘。

我们将选记为1，不选记为0。盘还是不盘？这是个问题。

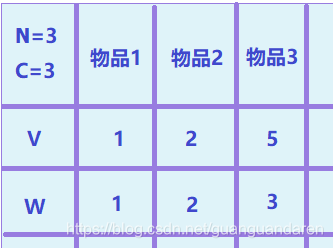
下面我们以本题的输入样例作为例子(始值改为3 3 0）：

初步了解01背包问题（分治篇） )

假定背包容量c=3，物品数n=3，它们的价值(v)和重量(w)如上图。现在要从中选择物品装入背包中，要求物品的重量不能超过背包的容量，并且最后放在背包中物品的总价值最大。

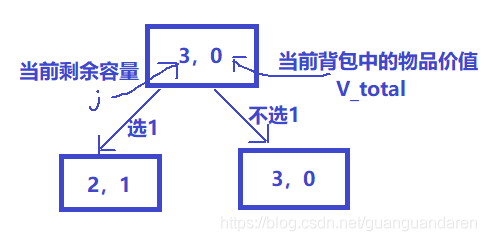
对于物品1，背包的当前容量为3>1，因此有两种选择。当我们选择一个物品的时候，背包的容量会减少，但是里面的物品总价值会增加。就像下面这样：

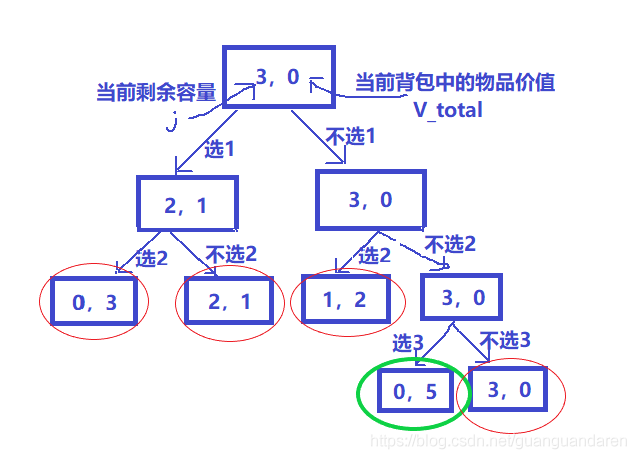
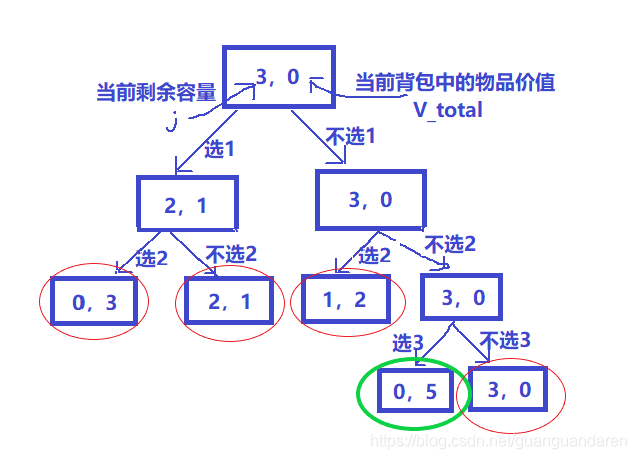
初步了解01背包问题（分治篇） )

这样就分出了两种情况，我们继续进行选择。如果我们选择了物品1，那么对于物品2，当前剩余容量为2，也可以选或者不选。可见，我们每次对物品做出一次选择，上面的一种可能就会分裂成两种。让我们继续画下去，最终就会形成我们的决策树。

初步了解01背包问题（分治篇） )

最后，我们在这棵决策树上(每个被圈中的方框都是待选的结果）通过比较得到最大值5。

（注：图中本应有9个待选结果，由于有四个容量不足，无法继续分裂更多可能）

值得说明的是，通常在问题中会更有更多复杂的用例，建议读者可以仿着画一次图，以便理解。

分治法

接下来，我们将问题扩展到一般情况。为了实现这个目的，我们需要将问题进行抽象并建模，然后将其划分为更小的子问题，找出递推关系式。

问题抽象：我们对第 i 个物品的选择定义为 xi(选为1，不选为0）,vi代表第i个珠宝的价值，wi代表第i个珠宝的重量。

约束条件：x1w1 + x2w2 + x3w3 + ... + xnwn < c。对于上面的例子，则为1x1+2x2+3*x3<=3

建模：题目要求找出x1v1 + x2v2 + x3v3 + ... + xnvn 中的最大值

定义函数：V_total(i,j)：表示当前背包剩余容量为j 时，前i 个物品最佳组合所对应的价值。

需要可以说明的是：原问题是要求出【**将n件物品放入容量为c的背包的最优价值】；**

现在，我们来考虑一下子问题：

我们将前*i* 件物品放入容量为*j* 的背包，所得到的最优价值为V_total(i,j)。如果只考虑第i件物品放还是不放，那么就可以转化为一个只涉及到前i-1个物品的问题。

如果不选第i个物品，那么问题就转化为“前i-1\件物品放入容量为j的背包中的最优价值组合”，对应的值为V_total(i-1,j)。如果放第i个物品，那么问题就转化成了“前i-1件物品放入容量为j-wi的背包中的最优价值组合”，对应的值为V_total(i-1,j-wi)+vi。

为避免看不懂，这里再次放出这张决策图。（建议自己另画一张进行分析）。

初步了解01背包问题（分治篇） )

怎么判断一个物品选还是不选呢？经过了上述分析，我们知道对于第i 个物品，我们有以下两种情况：

①若背包剩余容量不足以容纳这个物品，则背包的价值与前i-1个物品的价值相同，即V_total(i,j) = V_total(i-1,j)
②若背包剩余容量足以装下物品，则判断选或者不选背包中物品价值的大小，选出较大的一个。

即Max{V_total(i-1,j-wi) + vi, V_total(i-1,j)}

于是有如下的递推关系：

初步了解01背包问题（分治篇） )

现在，我们可以照着这个递推关系，从i=n,j=c开始，写出递归解法的关键部分：

int V_total(int i,int j){//通过递归找出最优的组合
    if(j<w[i])
        return V_total(i - 1, j);
    else
        return max(V_total(i - 1, j), V_total(i - 1, j - w[i]) + v[i]);

}

初步了解01背包问题（分治篇）

没想到吧，竟然如此简单？(完整代码还要判断一下n==0或c==0的情况,由于重点不在这，就不附代码了）

总结

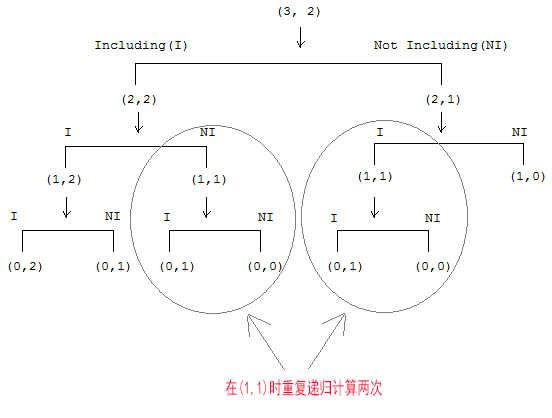
我们通过将大问题拆分成小问题，并寻找问题中的递推关系，解决一个个小问题，最终成功解决原问题。但由于分治法在子问题和子子...问题过程中进行了多次的重复计算（尝试每个组合的方法的问题是重复步骤，因为它存在重叠的子问题）如下图：

初步了解01背包问题（分治篇） )

因此这种方法具有重复的计算和时间复杂性是指数的。（指数级别是由树的深度depth决定的）

为了找到更好的解决方案，我们将在下一篇文章中学习动态规划算法。动态规划具有记忆性，一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。通过填写表把所有已经解决的子问题答案纪录下来，在新问题里需要用到的子问题可以直接提取，避免了重复计算，从而节约了时间。它试图仅对每个子问题解决一次，从而减少计算量。（所以在问题满足最优性原理(见下文)之后，用动态规划解决问题的核心就在于填表，表填写完毕，最优解也就找到。）这种做法在重复子问题的数目关于输入的规模呈指数增速时特别有用。

下面进入正题，请看下一篇文章：基于01背包问题的动态规划算法

本文转自 https://blog.csdn.net/guanguandaren/article/details/107940122，如有侵权，请联系删除。