这两天c++的习题开始不考察c++了，开始考察动态规划问题，唉，没学过动态规划算法来编这题目真是一把辛酸泪，下面给出题目（题目来源：郭玮老师的mooc）
2:Charm Bracelet
查看 提交 统计 提问
总时间限制: 1000ms 内存限制: 65536kB
描述
Bessie has gone to the mall’s jewelry store and spies a charm bracelet. Of course, she’d like to fill it with the best charms possible from the N(1 ≤ N≤ 3,402) available charms. Each charm iin the supplied list has a weight Wi(1 ≤ Wi≤ 400), a ‘desirability’ factor Di(1 ≤ Di≤ 100), and can be used at most once. Bessie can only support a charm bracelet whose weight is no more than M(1 ≤ M≤ 12,880).

Given that weight limit as a constraint and a list of the charms with their weights and desirability rating, deduce the maximum possible sum of ratings.
输入
Line 1: Two space-separated integers: N and M
Lines 2…N+1: Line i+1 describes charm i with two space-separated integers: Wi and Di
输出
Line 1: A single integer that is the greatest sum of charm desirabilities that can be achieved given the weight constraints
样例输入
4 6
1 4
2 6
3 12
2 7
样例输出
23
看上去这题确实不难，真正的题目就是给定总重量m，求最大的desirability。然后我一下子想到只要遍历一下所有情况，然后取出weight满足的情况中desirability最大的即可，贴出我写的代码：

#include <iostream>
#include <cstring>
#define MAX 3402
using namespace std;

class charm;
int combine_decrease(int m , charm* arr, int start, int* result, int count, const int NUM);

class charm
{
public:
    int w;
    int d;
};


int main (void)
{
    int n;
    int m;
    int i;
    int j ;
    int max_desir = 0;
    int temp = 0;
    charm charm_list[MAX] ; 
    int result[MAX] ;
    cin>>n>>m;
    for(i=0;i<n;i++){
        cin>>charm_list[i].w>>charm_list[i].d;
    }//have stored the charm;
    for(i = 1;i <= n; ++i){
        temp = combine_decrease(m,charm_list , n , result , i , i );
        if (temp >= max_desir)
            max_desir = temp;
    }
    cout<<max_desir;

}


//arr涓哄師濮嬫暟缁?
//start涓洪亶鍘嗚捣濮嬩綅缃?
//result淇濆瓨缁撴灉锛屼负涓€缁存暟缁?
//count涓簉esult鏁扮粍鐨勭储寮曞€硷紝璧疯緟鍔╀綔鐢?
//NUM涓鸿閫夊彇鐨勫厓绱犱釜鏁?
int combine_decrease(int m, charm* arr, int start, int* result, int count, const int NUM)
{
  int i;
  int sum = 0;
  int temp = 0;
  int temp_weight = 0; 
  for (i = start; i >=count; i--)
  {
    result[count - 1] = i - 1;
    if (count > 1)
    {
      temp = combine_decrease(m,arr, i - 1, result, count - 1, NUM);
      if(temp >= sum){
        sum = temp;
      }
      temp = 0;
    }
    else
    {
        int j;
        for (j = NUM - 1; j >=0; j--){
            temp_weight +=arr[result[j]].w;
            temp += arr[result[j]].d;
            //printf("%d ",arr[result[j]].d);;
            if(temp_weight > m) break;
        }
        //cout<<endl;
        //cout<<"desire:"<<temp<<"weight:"<<temp_weight<<endl;
        if(temp>=sum && temp_weight <= m)
            sum = temp;
        //cout<<"sum:"<<sum<<endl;
        temp = 0;
        temp_weight = 0;
    }
  }
  return sum;
}

答案确实是做出来了，应该也是对的，然后提交后出现**“超时”**，唉想想也是，遍历所有情况，想想都害怕，还用递归来实现，机子肯定要爆掉。没办法实在想不出，上网查资料。
一查就查到了，这是经典的01背包问题，也就是经典的动态规划求解问题：
代码来源https://blog.csdn.net/qingboda110/article/details/51050299

#include<stdio.h>
int W[3500];
int D[3500];
int f[13000];
int main(){
    int ans,max,n,i,j;
    scanf("%d",&n);
    scanf("%d",&max);
    for(i=0;i<n;i++){
        scanf("%d",&W[i]);
        scanf("%d",&D[i]);
    }
    for(i=0;i<n;i++){
        for(j=max;j>0;j--){
            if(j>=W[i]&&f[j]<f[j-W[i]]+D[i])
                f[j]=f[j-W[i]]+D[i];
        }
    }
    ans=0;
    for(i=0;i<=max;i++){
        if(f[i]>ans)
            ans=f[i];
    }
    printf("%d\n",ans);
    return 0;
}

一提交果然成功，但是看着代码依然无法理解，继续查资料，发现了这篇博文，讲的很好，看了半小时终于搞懂了，01背包问题，给出博文地址：https://www.cnblogs.com/wujing-hubei/p/6376218.html?utm_source=tuicool&utm_medium=referral
动态规划的思路，还是用小问题的解决去解决大问题，然后关键就在于找到大问题到小问题的简化关系：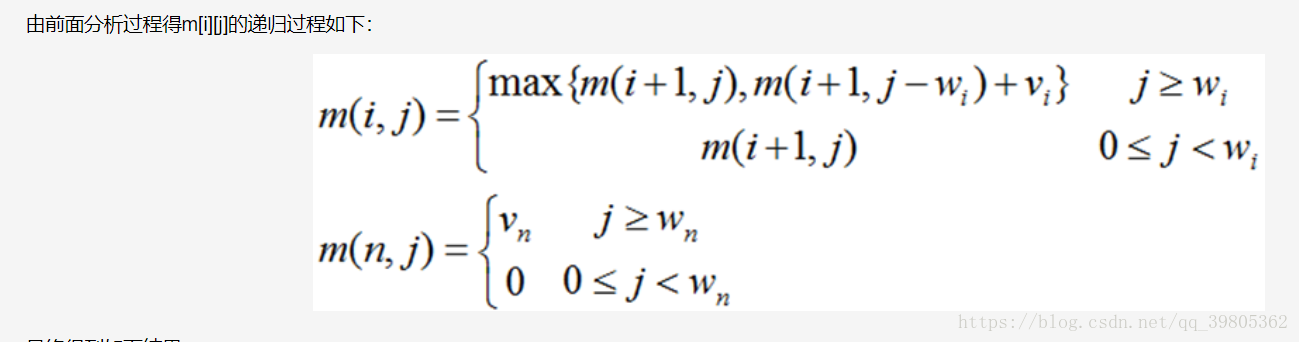

在此谢过博主的帮助了。