01
题目信息
题目地址：
https://leetcode-cn.com/problems/validate-binary-search-tree/
给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入: 2 / \ 1 3 输出: true
示例 2:
输入: 5 / \ 1 4 / \ 3 6 输出: false 解释: 输入为: [5,1,4,null,null,3,6]。 根节点的值为 5 ，但是其右子节点值为 4 。
02
解法一：递归
和上题一样可以很好的想到递归的思路，左边都是越来越小，右边是越来越大。这个地方容易产生一种错觉。
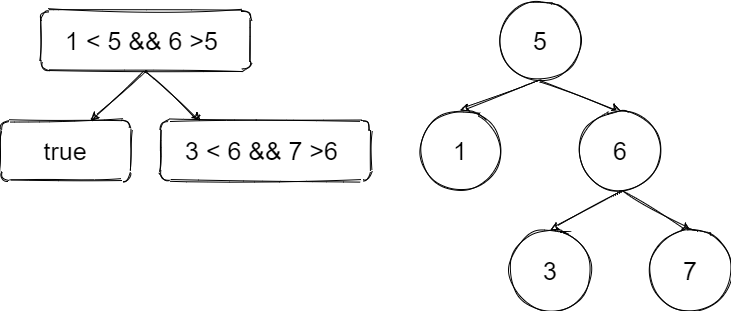
1
错误思路及代码：
就是只比较左右子节点的与父节点大小关系，如上图第一次是满足的，接下来递归左节点但他没有子节点结束并返回true,递归右节点也满足关系，继续递归其右节点因无子节点结束，左边同理。整个递归完成最终是true,但因为3比根节点5小应该在左子树不满足二叉搜索树
public boolean isValidBST(TreeNode root) { if(root == null) return true; if(root.left != null && root.left.val >= root.val) return false; if(root.right != null && root.right.val <= root.val) return false; return isValidBST(root.left) && isValidBST(root.right); }
那么问题就在于我们要比较的东西是什么？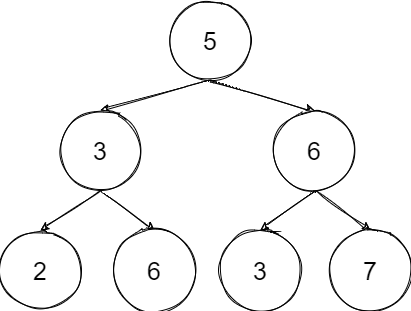
对于叶子节点2来说它比3小就可以没有限制，对于叶子节点6的位置它只能大于3并且小于5才有效 也就是说我们往左边走即是小那么就有一个上限之后不能超过，往右边走即是大就有一个下限。
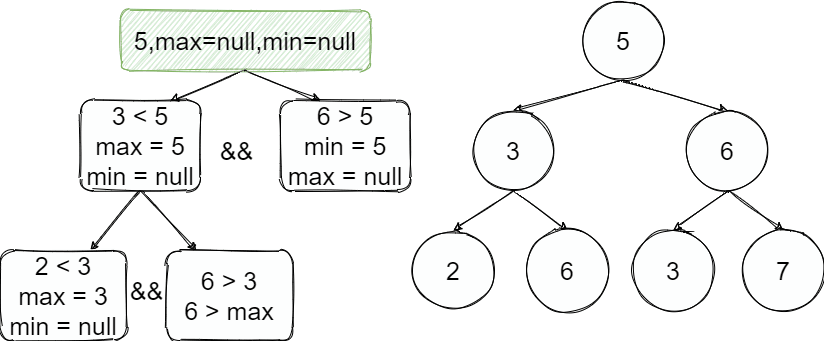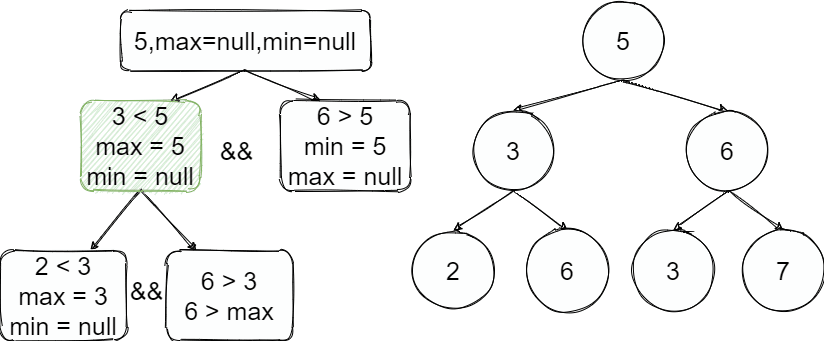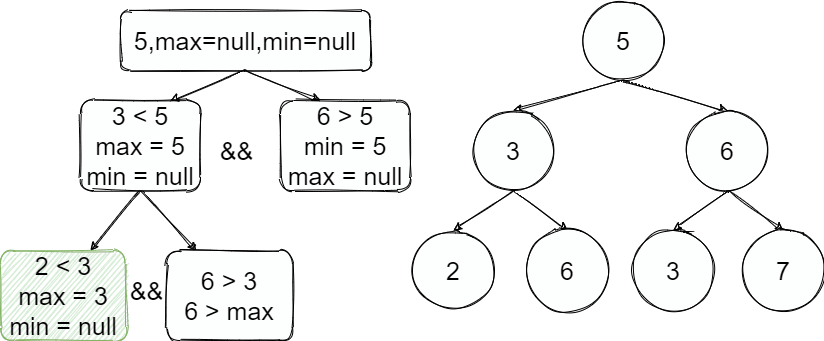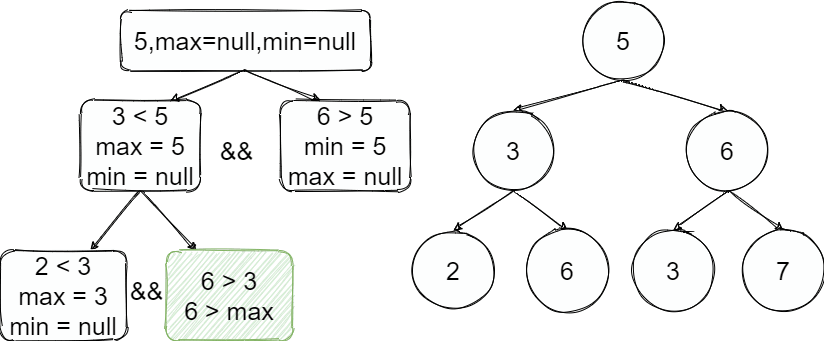
3
按照整个过程如上图，从根节点开始往左进入递归，往左了以后这边的值都小于上限5并且3满足小于5继续递归找到2也是满足并且2之后的树上限是3，继续递归为空了出去，执行下一步的兄弟节点判断时超过了上线结束
代码如下：
public boolean isValidBST(TreeNode root) { return process(root, null, null); } //递归方法 public boolean process(TreeNode node, Integer min, Integer max) { if (node == null) return true; if (min != null && node.val <= min) return false; if (max != null && node.val >= max) return false; if (!process(node.right, node.val, max)) return false; if (!process(node.left, min, node.val)) return false; return true; }
4
03
解法二：中序遍历
中序遍历是树的一种遍历方式，先数左子树在数中间在数右子树，那么通过中序遍历如果是真的二叉搜索树是一个从小到大的序列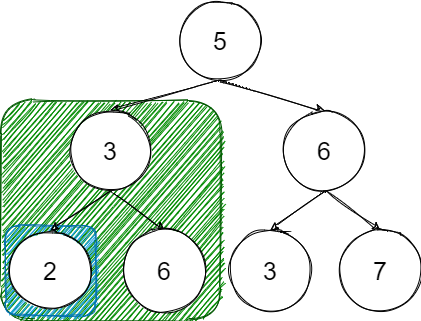
上图中序遍历：[2,3,6,5,3,6,7]
//记录前一个 Integer pre = null; public boolean isValidBST(TreeNode root) { if (root == null) return true; // 访问左子树 if (!isValidBST(root.left)) return false; // 访问当前节点：如果当前节点小于等于中序遍历的前一个节点.即不满足 if (pre != null && root.val <= pre) return false; pre = root.val; // 访问右子树 return isValidBST(root.right); }
6
04
总结
其实两种解法也都是属于深度优先，一个在过程中处理遍历方式为后序，一个是中序。使用不同的遍历过程那么就需要想清楚在这种遍历下处理判断逻辑。
本文分享自微信公众号 - IT那个小笔记（qq1839646816）。
如有侵权，请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。
