完整示例代码请移步至GitHub | Gitee

如有错误，还请指正。

微信扫描下方二维码，一起学习更多计算机基础知识。

1.0. 什么是线性表？

所谓线性，即一条线，这条线可以是直线，也可以是曲线。

所谓表，肯定都不陌生，生活中有各种各样的表或者表格。我们在表格中填写各种各样的信息，通过表格，能够很好地对信息进行分类储存和分析。

表的特点有：

• 表由若干单元格组成
• 单元格之间有顺序
• 除特殊位置的单元格（首起和结尾）有一个“邻居”外，其他单元格都有两个“邻居”。

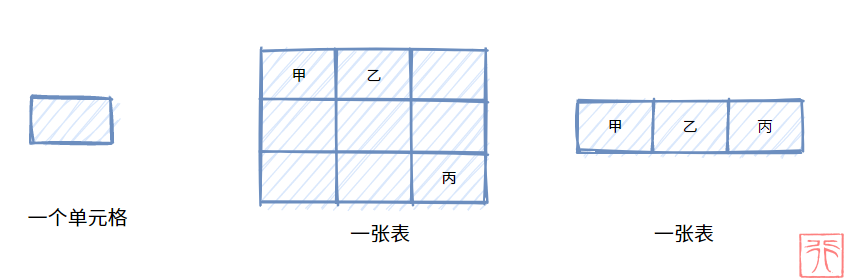
那么什么是线性表呢？简单来说，就是使用“直线”或“曲线”连接起来的表。

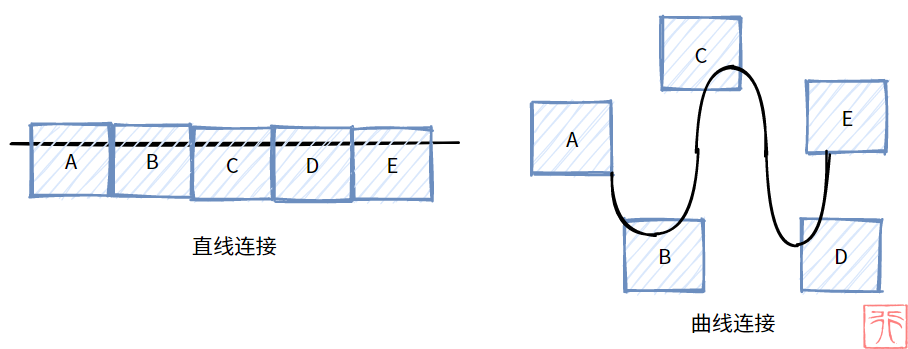
明确几个名词：

• 我们在表中称呼的“单元格”，在线性表中可以称之为元素。
• 对于某个元素，在其前邻的元素称之为直接前驱元素，在其后邻的元素称之为直接后继元素。
• 线性表中元素的个数称之为线性表的长度。
• 第一个元素称之为首元素，最后一个元素称之为尾元素。

由上图可以总结出线性表的特点：

• 线性表由若干元素组成，用来存储信息。
• 元素之间有顺序。
• 除了首元素（只有一个直接后继元素）和尾元素（只有一个直接前驱元素）外，其它元素都有且仅有一个直接前驱元素和一个直接后继元素。简单来说，即元素之间只能由一对一的关系。

总结一下，线性表是由若干元素按线性结构（一对一的关系）组成的有限序列。

1.1. 线性表的顺序存储结构

不管数据结构的形式再怎么变，数据结构的最根本的目的始终不会变，那就是为了更高效地对数据进行存储、修改、删除和访问，这种高效通常体现在时间上和空间上，也即程序运算速度快慢和所用存储空间的少多。

那么线性表这种数据结构是如何进行存储的呢？前面介绍了一种“用直线连接”的线性表，“直线”只是形象化的语言，实际上的存储中是不会有所谓“直线”这种东西的。

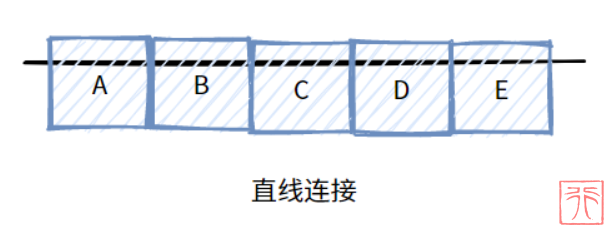
所谓“直线连接”即顺序存储，那么什么是顺序存储呢？

首先得先解释一下什么是内存。内存是计算机的存储器的一种，它扮演着非常中要的角色。世上的一切东西，即使是虚拟的，也需要有物理的实体作为载体。

举个例子，孩子们的玩耍需要有土地来承载，公园、游乐园等都是这种载体。没有土地作为载体，再活泼的孩子也没法活泼起来。对于代码来说，内存就是玩耍时需要的那块土地。

总之，内存就是代码运行时各种信息数据的载体空间。有了内存，我们才能施展拳脚。

既然涉及到空间，那该空间的东西肯定会以某种形式排列起来。通常来说，无外乎“整齐划一”和“杂乱无章”两种形式。

比如，一群孩子肩并肩地站成一排，占据一定的连续土地。

反映在内存中，就是数据紧密相接，占据一定的连续内存。

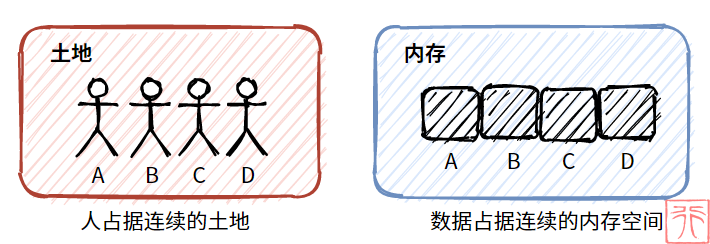
这种“占据连续的内存空间”即为顺序存储方式。

可以把内存比作一幢大楼，楼中有许多房间，每个房间都有房间号，一个房间刚好住一个人。当 A、B、C、D 四位小朋友来到大楼里，选了连续的 4 个房间分别入住，那么我们就可以认为，这四位小朋友是“顺序入住”的。

内存 = 大楼，房间 = 内存单元，房间号 = 内存地址，入住的人 = 要存储的数据。

反映在内存中，所谓顺序存储，即用一段连续的内存单元分别存储线性表中的数据。

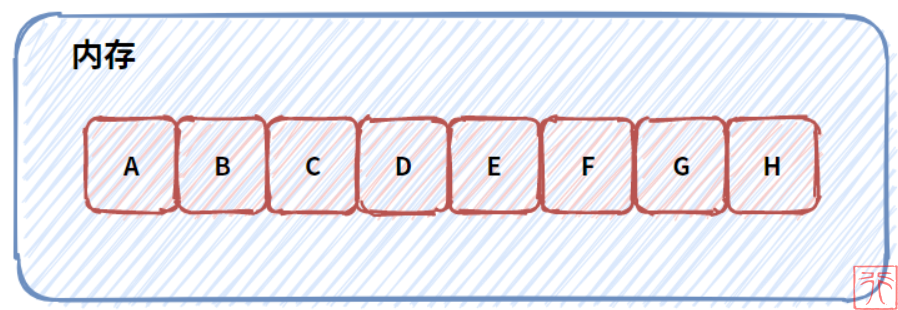
如上图所示，线性表的顺序存储是在内存空间中开辟一块连续的空间，开辟好之后，这块空间就被这个线性表“占用”了。

这种顺序存储结构的线性表我们可以称之为顺序表。

1.2. 顺序表的实现思路

线性表的每个数据元素的类型都相同、数据元素个数有限。根据这个特性我们很容易想出可以用一维数组来实现顺序存储结构。

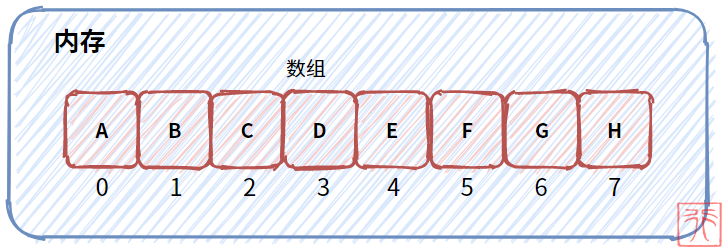
注意：是先占用再使用，也即线性表的长度不能超过最大存储容量（数组的长度）。

如何用代码表示一个用数组实现的线性表？首先搞清楚一个这样的线性表有哪些必要的东西。

1. 线性表需要一个数组用来存储数据元素；
2. 线性表需要一个最大存储容量（数组长度），即你想要“占”多少个位子，是要事先声明的，不再轻易改变；
3. 线性表需要一个长度用来表示存了多少数据元素，线性表的长度随着数据的增删而变化，没有这个就可能导致你“塞”的数据比“占”的位子多，而“溢”出来。

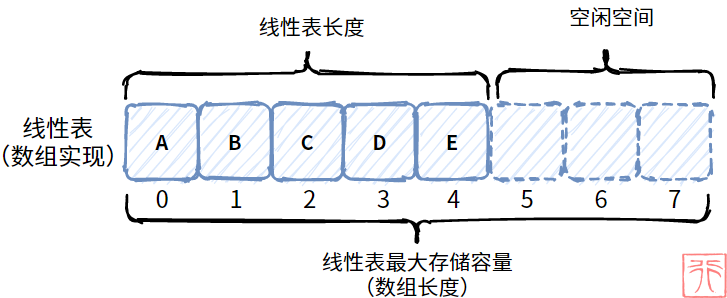
总结一下，一个顺序表 (ArrayList) 由以下三部分组成：

1. 用来实际存储数据的数组——data[]；
2. 用来表示线性表的最大存储容量的值——MAXSIZE；
3. 用来表示线性表的长度的值——length。

1.3. 顺序表的具体实现

有了上面的分析，下面就可以使用 C 语言的结构体来实现顺序表了。

为了说明问题简单，我们这里的顺序表只存储整数。

#define MAXSIZE 10 //顺序表的最大存储容量

typedef struct {
    int data[MAXSIZE]; //存储数据的数组
    int length; //顺序表的长度
} ArrayList;

这样的一个结构体就能完美地表示一个顺序存储结构的线性表了。

1.4. 顺序表的初始化

孩子们已经知道公园了在哪了，但还未踏上去。

到此为止，我们已经知道了什么是顺序存储，也知道了如何用代码表示顺序表，但仅停留在“知道”这一步，我们还未将其实际地“创造”出来放到内存中。

要想使用一个顺序表，那么我们得先声明一个顺序表，然后将其初始化为空顺序表，也即 length = 0：

/**
 * 初始化顺序表，将线性表的长度置为0
 * list : 要操作的顺序表的地址
 */
void init(ArrayList *list)
{
    list->length = 0;
}

注意：我们要改变顺序表的长度 length，所以要传给 init 函数的参数是一个 ArrayList 类型的指针。

ArrayList list; //声明顺序表list
init(&list); //初始化list

1.5. 顺序表的插入和删除

现在孩子们已经来到公园了，并且已经肩并肩地排好队开始玩游戏了，现在有一名小伙伴想要加入到队伍中和他们一块玩。所以有一部分孩子为他“腾”出了位置，让他“插队”。

由于 甲 要站在 B 的后面，所以 C、D、E 都要后退一个位置给 甲“腾空位”，然后 甲 才能“插队”到 B 后面。

可以把孩子们站成的队伍看成线性表，把孩子看成元素，下图所示过程就是顺序表的插入元素的操作过程。

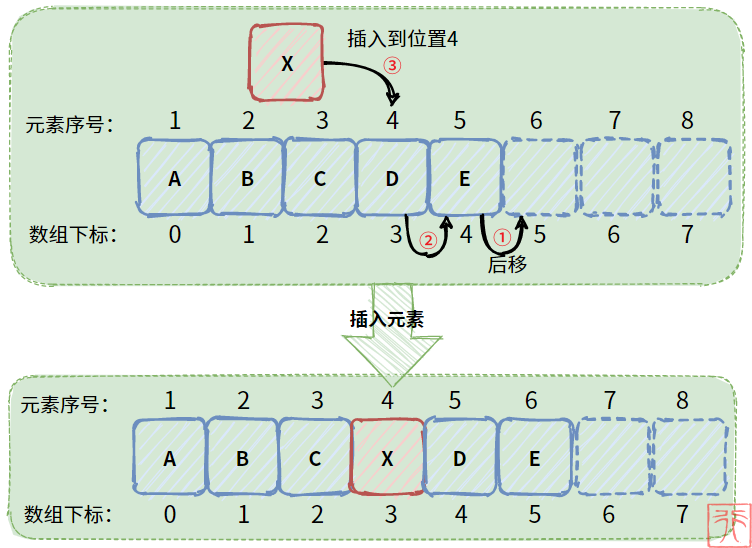
孩子们从最后一个人开始逐个后退，后退到需要的空位为止，线性表的元素也是如此，不过线性表是使用“向后赋值”来实现“后退”的效果的。

分析到此，代码就可以写出来了。

/**
 * 向顺序表的指定位置插入指定值
 * list : 顺序表的地址
 * position : 要插入的位置 (1 <= position <= list->length + 1)
 * elem : 要插入的值
 * return 0 : 插入失败；return 1 : 插入成功
 */
int insert(ArrayList *list, int position, int elem)
{
    if (list->length == MAXSIZE) {
        printf("顺序表已满\n");
        return 0;
    }
    if (position < 1 || position > list->length + 1) {
        printf("插入位置不合法\n");
        return 0;
    }
    for (int i = list->length - 1; i >= position - 1; i--) {
        list->data[i + 1] = list->data[i]; //向后赋值
    }
    list->data[position - 1] = elem;
    list->length++;
    return 1;
}

注意：

1. 需检查顺序表是否已满（length 是否等于 MAXSIZE）
2. 需检查插入位置是否合法（不能插入到表外）
3. 插入成功后，顺序表的长度要加一

现在，刚刚插队的小孩被妈妈喊回家吃饭了，所以他需要离开队伍，这时队伍中“空出”了一个位置，所以他后面的小孩都自觉的向前一步走，使队伍更紧凑。

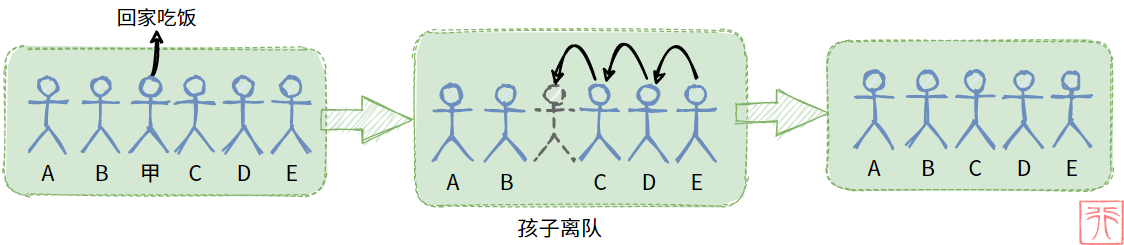
孩子离队后，“空位”之后的每个孩子都逐个“向前一步走”。线性表删除元素时，使用“向前赋值”来实现孩子“向前一步走”的效果。删除操作和插入操作刚好相反，下图是其过程：

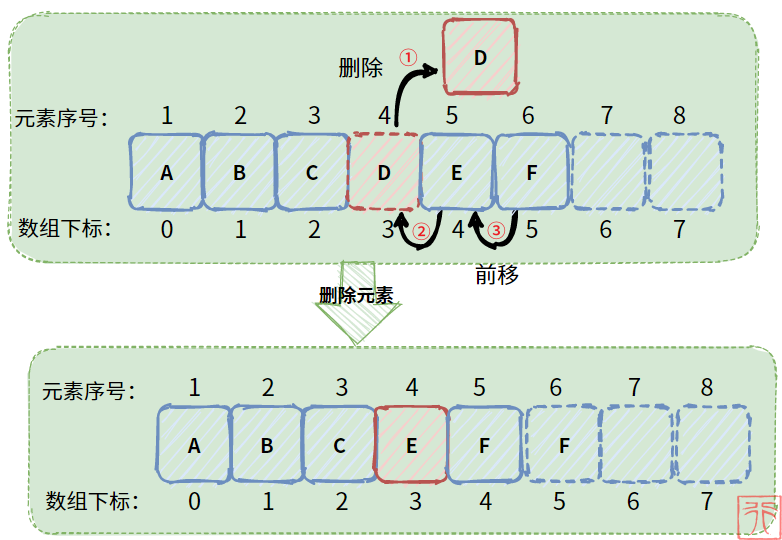
下面是代码实现：

/**
 * 删除指定位置的元素，并保存其值
 * list : 顺序表的地址
 * position : 要删除的元素位置
 * elem : 保存变量的地址
 * return 0 : 删除失败；return 1 : 删除成功
 */
int delete(ArrayList *list, int position, int *elem)
{
    if (list->length == 0) {
        printf("顺序表为空\n");
        return 0;
    }
    if (position < 1 || position > list->length) {
        printf("删除位置不合法\n");
        return 0;
    }
    *elem = list->data[position - 1];
    for (int i = position - 1; i < list->length - 1; i++) {
        list->data[i] = list->data[i + 1];
    }
    list->length--;
    return 1;
}

同样注意：

1. 需检查顺序表是否为空
2. 需检查删除位置是否合法
3. 删除成功后，顺序表长度要减一

1.6. 顺序表的其他操作

至此，已经介绍了基本的“增、删、改、查”的“增和删”。

至于“改和查”，由于顺序表是用数组来实现的，而数组的查询和修改是及其方便的，如：

int a = array[1]; //查询
array[2] = 5; //修改

所以，顺序表的查询和修改也极为方便。

下面是查询的代码：

/**
 * 查询指定位置的元素
 * list : 要操作的顺序表
 * position : 要查询的元素位置
 * elem : 保存变量的地址
 * return 0 : 查询失败；return 1 : 查询成功
 */
int get(ArrayList list, int position, int *elem)
{
    if (list.length == 0) {
        printf("顺序表为空\n");
        return 0;
    }
    if (position < 1 || position > list.length) {
        printf("位置不合法\n");
        return 0;
    }
    *elem = list.data[position - 1];
    return 1;
}

下面是更新的代码：

/**
 * 更新指定位置的元素
 * list : 要操作的顺序表的地址
 * position : 要更新的元素位置
 * elem : 要更新的值
 * return 0 : 更新失败；return 1 : 更新成功
 */
int update(ArrayList *list, int position, int elem)
{
    if (list->length == 0) {
        printf("顺序表为空\n");
        return 0;
    }
    if (position < 1 || position > list->length) {
        printf("位置不合法\n");
        return 0;
    }
    list->data[position - 1] = elem;
    return 1;
}

以上即为针对顺序表最基础的增删改查操作，会了这四种，其他的操作也基本上可以触类旁通了。

1.7. 顺序表的优缺点

上面的那个小孩加入队伍的时候，为了给他腾位置，很多人都而向后退一步。但是才玩了一会，他就被叫回去吃饭了，之前向后退步的人又不得不再向前走一步。因为一个人，而导致很多人不得不为之变动，小孩们很不乐意。

写过上面四个函数，我们也会有小孩们的体会。

增加和删除一个元素太麻烦了，当元素很少还不明显，但当有成百上千个元素时，就需要移动大量的元素了，很麻烦，我们很不乐意。

查询和修改一个元素却很简单，这是数组的功劳。

另外，线性表的容量是固定的，大多数情况下，我们并不会提前知道线性表的容量，所以容量的分配是一个很大的问题，少了不够用，多了太浪费。像极了在快速长身体的青春期时买衣服的你。

总结一下：

优点：

• 查询和修改元素方便快捷

缺点：

• 增加和删除某个元素需要移动大量的其他元素
• 难以确定容量大小（所以通常会尽可能分多一点来“兜底”，但这极易造成浪费从而影响性能）