完整示例代码请移步至GitHub | Gitee

如有错误，还请指正。

微信扫描下方二维码，一起学习更多计算机基础知识。

8.0. 何为查找？

我们平常做很多事情，都会涉及到大量的增删改查操作。比如一个用户管理系统，会涉及用户注册（增）、用户注销（删）、修改用户信息（改）、查找用户（查），其中“删”和“改”要依赖“查”操作。

下面重点来介绍一下查找这个重要的操作。

现给你一个点名册，让你查找一个学生。我们的做法是：根据这个学生的姓名或者学号，在点名册中一个个的比对，直到找到一个学号或姓名符合条件的学生为止，否则就可以说点名册中没有该学生。

学号	姓名	专业
101	张三	键盘清洁与维修
102	李四	母猪产后护理与保养
103	李四	计算机开关机专业操作员

点名册是一个集合，也可称之为查找表，其中有大量同一类型的元素，也可称之为记录——学生。学生中可能有重名的，但不会有重学号的，也即，一个学号唯一对应一个学生，一个姓名可能对应多个学生。如果我们根据学号找，只要点名册中有，那么就可以找到唯一一个符合条件的学生。如果我们根据姓名找，那么我们就可能找到多个符合条件的学生。

像学号和姓名这种可以标识一个学生的值，我们称之为关键字，学号这种唯一标识一个元素的值为主关键字，姓名这种可能标识若干元素的值为次关键字。当集合中的元素只有一个数据项时，其关键字即为该数据元素的值。

比如数组[1, 2, 3, 4, 5, 6, 7, 8, 9]，其元素只有一个数据项，关键字即元素值本身；而点名册中的元素——学生，却有三个数据项——学号、姓名、专业，其中学号、姓名为关键字。

如果你学过数据库，那么以上概念很容易理解。

所谓查找，通俗点说就是在一大群元素（集合 / 查找表）中，依照某个查找依据，找一个特定的、符合要求的元素（记录）。

• 如果找到了，即查找成功，返回元素的信息；

• 如果找遍所有元素还没找到，说明这群元素中没有符合要求的元素，即查找失败，返回一个可以明显标记失败的值，比如“空记录”或“空指针”。

所谓查找依据，就是给定一个目标值，比较该目标值和关键字是否相等。这就要求目标值和关键字的类型要相同。

8.1. 顺序查找（Sequential Search）

顺序查找是我们最容易想到的查找方式，上面的点名册例子中，查找一个学生就是用的就是顺序查找。

顺序查找思想：

从集合中的第一个元素开始至最后一个元素，逐个比较其关键字和目标值。

• 若某个关键字和目标值相等，则查找成功，返回所查元素的信息；
• 若没有一个关键字和目标值相等，则查找失败，返回失败标识值。

比如，给定一个数组[11, 8, 4, 6, 9, 1, 16, 22, 14, 10]，给定目标值 key，若找到，则返回其数组下标；否则，返回 -1：

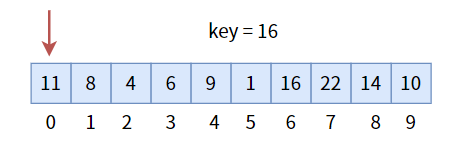
只需从下标 0 开始遍历整个数组进行比较即可：

/**
 * @description: 从头到尾遍历整个数组，查找目标值 key，返回其下标 index        
 * @param {int} *array 数组 为了说明问题简单，这里的数组元素不重复
 * @param {int} length 数组长度
 * @param {int} key 目标值
 * @return {int} 如果找到，返回目标值下标；否则返回 -1
 */
int sequential_search(int *array, int length, int key)
{
    for (int index = 0; index < length; index++) {
        if (array[index] == key) {
            return index;
        }
    }
    return -1;
}

以上代码存在可优化的地方，因为每次比较之前要判断数组是否越界：index < length，增加哨兵则可以避免这一步比较。

所谓哨兵，是一种形象的说法，将其放在数组头或尾，用来标记结束，当遍历到“哨兵”时，就说明数组中没有目标值，查找失败。

为此，我们要特意在数组中留出一个位置给“哨兵”，并且把哨兵的值设置为目标值：

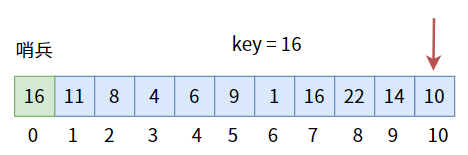
像这样，从另一侧往“哨兵”一侧遍历。如果数组中有目标值，则一定能找到；如果数组中没有目标值，那么就会遍历至“哨兵”而停下，因为“哨兵”的值就是目标值，所以返回下标为 0 时，意味着查找失败。

/**
 * @description: 顺序查找改进，增加哨兵
 * @param {int} *array array[0] 不存放数据元素，充当哨兵
 * @param {int} length 数组长度
 * @param {int} key 目标值
 * @return {int} 返回0，即哨兵下标，则查找失败；否则成功
 */
int sequential_search_pro(int *array, int length, int key)
{
    array[0] = key; // 哨兵
    int index = length - 1;
    while (array[index] != key) {
        index--;
    }
    return index;
}

在一侧放置“哨兵”的做法避免了每次遍历进行的数组越界检查，这样能提高效率。你可能会问就一句比较能提高多少效率？蚊子腿再小也是肉，而且当数据量很多时，这些“蚊子腿”就会积累成“大象腿”了。

以上就是顺序查找的基本内容，虽然加了“哨兵”可以小小地优化一下，但当数据量极大时，仍然改变不了这种查找方法效率低下的事实。

因为我们是从一头到另一头“顺序遍历”，所以有时候可能目标值就在第一个位置，只查找一次就找到了，仿佛是天选之子；但有时候可能目标值在最后一个位置，那就需要把所有元素都查找一遍才行，当有千万、亿条数据时，这种就太可怕了。

当然，优点也有：算法简单好理解、适合数据量小的情况使用（使用时尽量把常用数据排在前面，这样可以提高效率）。

8.2. 二分查找（Binary Search）

回到上面举得那个点名册的例子，那样一个个地找学号或姓名实在是太慢了，有没有什么更快的方法呢？

其实，在日常生活中的点名册更多的是已排序的，比如按姓氏首字母、按学号大小排序，这样一来，在找名字或找学号的时候就能有一个大致的区域了，而不必从头到尾一个个地找。

所以，排好序的集合是便于查找的。下面介绍一种利用已排序的查找——二分查找（或折半查找）。

所谓二分查找，关键在“二分”“折半”上，顾名思义，不断将集合进行二分（折半）拆分，以此将集合拆分几个区域，然后在某个区域中查找。前提条件是集合中的元素是有序的（从小到大或从大到小），元素必须采用顺序表（数组）存储。

二分查找思想：

在有序顺序表中，取中间元素，将有序顺序表分为左半区和右半区，比较中间元素的关键字和目标值 key 是否相等：

• 如果相等，则查找成功，返回中间元素的信息；
• 如果不相等，说明目标值 key 在左半区或右半区：
  • 若目标值 key小于中间元素的关键字，则来到左半区；
  • 若目标值 key 大于中间元素的关键字，则来到右半区；

不断在各半区中重复上述过程，直到查找成功；否则，则集合中无目标值，查找失败。

下面结合实例，看一下具体过程。

这是一个有序（从小到大）的数组，我们要查找 33：

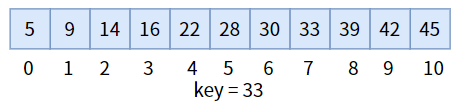
要想将数组分为左右半区，需要三个标致：最左标志位 left、最右标志位 right 和中间标志位 mid。其中 mid = (left + right) / 2，确定了 mid 的值之后，与目标值 key进行比较：

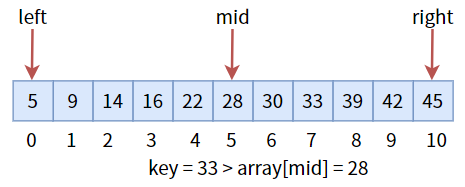
中间值 28 小于目标值key，说明目标值在右半区，所以更新三个标志位，进入右半区，然后继续比较：

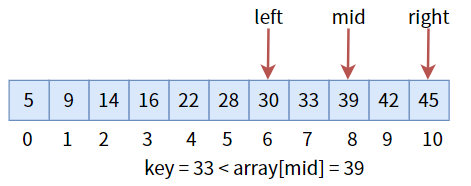
中间值 39 大于目标值key，更新三个标志位，进入左半区：

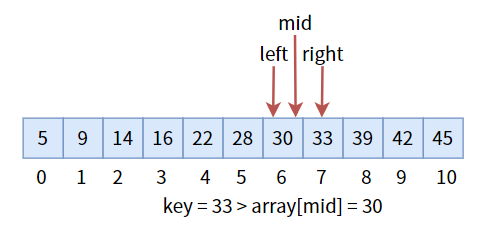
中间值 30 小于目标值key，更新三个标志位，进入右半区：

中间值 33 等于目标值key，返回其下标，即 mid。

具体代码如下：

/**
 * @description: 二分查找
 * @param {int} *array 有序数组
 * @param {int} length 数组长度
 * @param {int} key 目标值，和关键字比较
 * @return {int} 返回目标值下标；若查找失败，则返回 -1
 */
int binary_search(int *array, int length, int key)
{
    int left, mid, right;
    left = 0;
    right = length - 1;
    while (left <= right) {
        mid = (left + right) / 2; // 中间下标
        if (key < array[mid]) { // key 比中间值小
            right = mid - 1; // 更新最右下标，进入左半区
        } else if (key > array[mid]) { // key 比中间值大
            left = mid + 1; // 更新最左下标，进入右半区
        } else {
            return mid; // key 等于中间值，返回其下标
        }
    }
    return -1; //未找到，返回 -1
}

二分查找的精髓在于中间标志位 mid 把有序顺序表一分为二，通过比较中间值和目标值的大小关系，能够筛选掉一半的数据，相当于减少了一半的工作量。

上例只比较了四次，就找到了目标值，如果使用顺序查找，则需要八次。

可以看出，二分查找的效率相较于顺序查找有了很大提高，但美中不足的是二分查找必须要求元素有序。在元素的有序状态不变化或不经常变化的情景下，二分查找非常合适；但是如果涉及到频繁的插入和删除操作，就意味着元素的有序状态会被频繁破坏，这样一来，我们就不得不花精力去维护元素的有序状态，自然又会降低效率，所以要根据实际情况灵活取舍。

8.3. 二叉查找树（Binary Search Tree）

8.3.0. 是什么？

二叉查找树必须满足以下特点：

• 若左子树不为空，则左子树的所有结点值皆小于根结点值
• 若右子树不为空，则右子树的所有结点值皆大于根结点值
• 左右子树也是二叉排序树

如下图，是一颗二叉查找树：

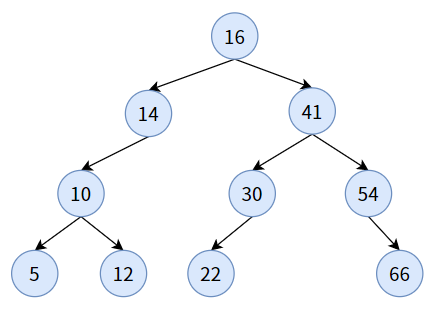
如果你对二叉查找树进行中序遍历，可以得到：5, 10, 12, 14, 16, 22, 30, 41, 54, 66。刚好是一个从小到大的有序序列，从这一点看，二叉查找树是可以进行排序的，所以这种树又叫二叉排序树（Binary Sort Tree）。

8.3.1. 查找

我们以上图为例，说明查找成功和失败两种过程。

先贴出代码：

int bst_search(BSTNode *root, int key, BSTNode **p, BSTNode *q)
{
    if (root == NULL) { // 空树，查找失败
        *p = q;
        return 0;
    } 
    if (key == root->data) { // 目标值相等根结点的值，查找成功
        *p = root;
        return 1;
    } else if (key < root->data) { // 目标值小于根结点的值，递归进入左子树
        return bst_search(root->left_child, key, p, root);
    } else { // 目标值大于根结点的值，递归进入右子树
        return bst_search(root->right_child, key, p, root);
    }
}

该方法中的三个指针的作用如下：

• 指针 root 始终指向根结点， 标识了与目标值比较的结点；

• 二级指针 p 指向最终查找的结果。如果查找成功，则指向“指向‘找到的结点’的指针”；如果查找失败，则指向“指向‘上次最后一个访问的结点’的指针”。

• 指针 q 初始为空，以后始终指向上一个根结点。

下面是查找成功的过程动图：

下面是查找失败的过程动图：

请注意，以上过程成立的前提是：二叉树是一颗二叉排序树，必须满足二叉排序树的三个特点。

所以，二叉排序树的“排序”二字是为查找而服务的，上面两个动图足以说明，排序方便了查找，因为每次比较都在缩小范围。

二叉排序树和二分查找本质上做的事是一样的，比如以下几方面：

1. 都是有序的。二分查找是全部有序，二叉排序数是局部有序。
2. 都是将一组数划分成若干区域。二分查找通过三个标志位，二叉排序树通过树结构。
3. 都是通过比较目标值和“区域分界点”的大小，从而确定目标值在哪个区域中。在二分查找中与中间标志位比较，在二叉查找树中与根结点比较。

我们在二分查找中说过：当涉及到频繁地插入和删除操作时，二分查找就不合适了。原因之一是二分查找要求元素是有序的（从小到大或从大到小），插入、删除破坏顺序后，需要额外精力维护有序状态。原因之二是二分查找使用顺序表实现，顺序表的插入和删除操作需要移动大量元素，也会影响效率。

但是二叉排序树是一个树，树结构通常使用链式结构来实现。链式结构对插入和删除操作很友好，也有利于我们维护二叉树的有序状态。

8.3.2. 创建和插入

现在给你一组没有顺序的数，比如 {16, 41, 14, 30, 10, 12, 54, 5, 22, 66}，如何创建出一颗二叉查找树（BST）？这里为了方便起见，我们约定二叉查找树中没有重复值。

所谓创建，即向一个空树中不断插入结点，从而构成一个非空的二叉查找树。所以关键在于如何向一个二叉查找树中插入结点。

所谓插入，即不断比较待插入结点和树中结点的值，使其插到合适的位置，怎么找到“合适的位置”呢？方法前面已经给出，即 bst_search。

如果我们在二叉查找树中查找待插入值，一定会查找失败，即 bst_search 一定返回 0，所以bst_search 方法中的 p 指针最终指向的是最后一个访问的根结点，这个根结点的左孩子或右孩子即是“合适的位置”。

下面是创建（插入）的过程动图，和查找失败的过程动图非常相似：

插入一个结点的代码如下，可以看出，和 bst_search 的代码很相似：

int insert_bst_node(BSTNode **p_root, int key)
{
    BSTNode *p;
    if (bst_search(*p_root, key, &p, NULL) == 0) { // 没有查找到 key
        BSTNode *new = create_bst_node(key); // 创建新结点
        if (p == NULL) { // 空树，新节点直接作为根结点
            *p_root = new;
            return 1;
        }
        if (key < p->data) { // 插入值小于 p 的值，插入到左子树
            p->left_child = new;
            return 1;
        }
        if (key > p->data) {  // 插入值大于 p 的值，插入到右子树
            p->right_child = new;
            return 1;
        }
    }
    return 0; // 插入失败
}

那么，创建操作用一个 for 循环就搞定了：

void create_bst(BSTNode **root, int *array, int length)
{
    // 循环向空二叉查找树中插入若干结点
    for (int i = 0; i < length; i++) {
        insert_bst_node(root, array[i]);
    }
}

8.3.3. 删除

至此，我们已经介绍过好几种数据结构了，每种都涉及到增加（插入）和删除操作。就像加法和减法一样，插入和删除操作可以看作是一对“反操作”。这意味着，它们在原理、代码上有相似之处，能够做到触类旁通。但这不是绝对了，必须具体问题结合具体环境进行具体分析。比如删除二叉查找树中的某个结点，可能会破坏二叉查找树的结构，破坏其顺序，所以我们就需要分情况讨论。

【情况一】

待删除的结点没有孩子，即删除叶子结点。这是最简单的情况，因为删除叶子不会破坏剩下的结构，也不会破坏剩下的结点的顺序。

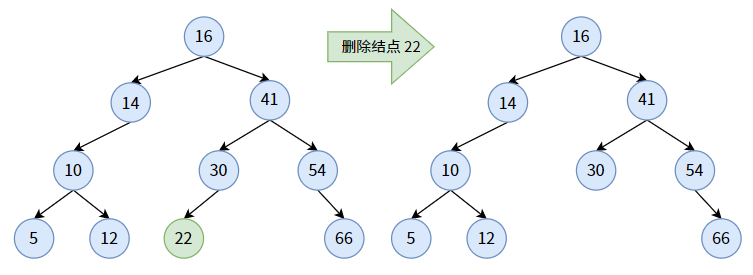
【情况二】

待删除的结点只有左子树或者右子树。这种情况也好做，将其左子树或右子树移动到删除结点处即可。由于二叉查找树使用了链式结构，所以删除操作的代价很小，只需要改变指针的指向。

【情况三】

待删除的结点既有左子树又有右子树。这种情况比较复杂，因为删除结点后，剩下了该结点的左子树和右子树“在风中飘荡”，一方面我们要维持树结构，另一方面我们要维持二叉查找树的结点大小顺序，所以删除结点会涉及到整个树结构的调整，即将“剩下的”左子树和右子树重新插到树结构中去。下面是过程：

从上图过程就可以看出，这有点太过打动干戈了。我们先是改变 结点 16 的右孩子指针，然后删除 结点 41，并将其右子树“摘出来”，然后把剩下的右子树中的所有结点重新插入到二叉查找树中。这样确实挺累人的。

不妨换一种思路：

我们将 32 赋值给结点 41，然后删除结点 32，同样能够达到删除结点 41 的效果。这种方式大大简化了操作，不需要移动甚至改变树的结构，代价较小。我称这种方式为——狸猫换太子。

那么为什么偏偏是把结点 32 赋值给待删除结点 41 呢？前面说过，二叉查找树的中序遍历是一个有序序列，这也是为什么叫它二叉排序树的原因。结点 32 刚好是结点 41 在中序遍历序列下的直接前驱结点，所以，将 32 赋值给结点 41 后，并不会影响二叉查找树的“左子树值小于根结点，右子树值大于根结点”的定义。

所以，如何找到待删除结点在中序序列下的直接前驱是关键。

在中序遍历序列下，根结点的直接前驱是其左子树中最右最下的那个结点，如上例中结点 41 的直接前驱是结点 32.

到此，如何写代码就很清晰了。

一、先递归地找到待删除结点：

/**
 * @description: 删除目标值结点
 * @param {BSTNode**} 二级指针，指向 指向树根结点的指针 的指针
 * @param {int} key 目标值
 * @return {int} 删除成功返回1；否则返回0
 */
int delete_bst_node(BSTNode **p_root, int key)
{
    if (*p_root == NULL) {
        return 0;
    }
    if (key == (*p_root)->data) { // 找到要删除的目标值 key
        rebuild_bst_after_delete(p_root);
    } else if (key < (*p_root)->data) { // 目标值小于根结点，递归进入左子树
        return delete_bst_node(&(*p_root)->left_child, key);
    } else { // 目标值大于右子树，递归进入右子树
        return delete_bst_node(&(*p_root)->right_child, key);
    }
}

可以看出，这段代码和删除操作的代码没有太大区别，本质仍是查找。

二、找到待删除结点后，将结点删除，然后调整以维持二叉查找树的结构：

/**
 * @description: 删除某个结点后重新调整二叉查找树
 * @param {BSTNode**} p_node 指向待删除结点的二级指针
 * @return {int} 成功返回1；失败返回0
 */
int rebuild_bst_after_delete(BSTNode **p_node)
{
    BSTNode *prev, *tmp;
    tmp = *p_node;
    if ((*p_node)->left_child == NULL) { // 左子树为空，重接右子树
        *p_node = (*p_node)->right_child;
        free(tmp);
        return 1;
    }
    if ((*p_node)->right_child == NULL) { // 右子树为空，重接左子树
        *p_node = (*p_node)->left_child;
        free(tmp);
        return 1;
    }
    // 左右子树均不为空
    if ((*p_node)->left_child != NULL && (*p_node)->right_child != NULL) {
        prev = (*p_node)->left_child;
        while (prev->right_child != NULL) { // 找到待删除结点的直接前驱
            tmp = prev;
            prev = prev->right_child;
        }
        (*p_node)->data = prev->data; // 赋值
        if (tmp != *p_node) { // 待删除结点有子孙结点
            tmp->right_child = prev->left_child;
        } else { // 待删除结点只有两个孩子结点，没有子孙结点
            tmp->left_child = prev->left_child;
        }
        free(prev);
        return 1;
    }
    return 0;
}