完整示例代码请移步至GitHub | Gitee

如有错误，还请指正。

微信扫描下方二维码，一起学习更多计算机基础知识。

7. 树（Tree）

7.0. 面临的问题

到目前为止，我们已经讲述了顺序表、链表、栈、队列四种数据结构，它们有一个共同的特点，就是它们都是线性表，换句话来说，它们都是线性结构，像一根绳子一样。

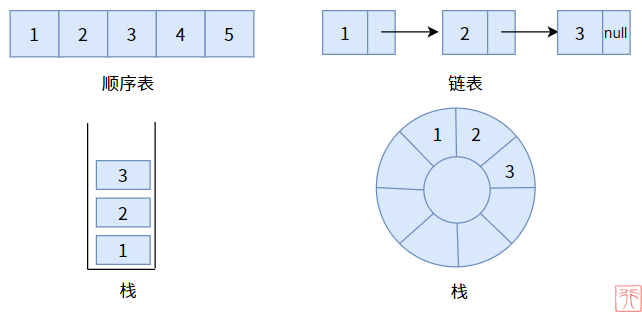
在 1.0. 什么是线性表？已经介绍过线性表的定义了，即由若干元素按照线性结构（一对一的关系）组成的有限序列。

关键词是一对一的关系。

显然，在复杂的现实社会中，这种一对一的关系是不能较好的满足我们的需求的。

比如说，父母和多个孩子之间的关系，一个父亲/母亲对应多个孩子，这显然不是一对一，而是一对多的关系。那么此时我们如何来描述这种一对多的关系呢？

当然是使用具有一对多关系的数据结构啦！有这种数据结构吗？有！本章就来介绍这种数据结构 —— 树。

7.1. 初识树

7.1.0. 什么是树？

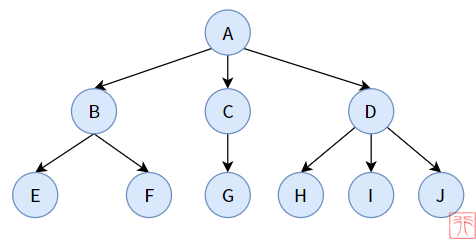
提到树（Tree），大家脑海中首先浮出的画面应该是类似这样的：

之所以我们会用“树”这个名词来命名具有“一对多关系”特性的数据结构，是因为树刚好能够很形象地诠释这种特性。我们来分析一下。

看一下上图中的树（土地以上的部分），它有一个树根，从树根开始往上分叉，主树干分叉成许多次树干，次树干又继续分叉为许多小树枝，小树枝上有许多叶子……

主树干对次树干、次树干对小树枝、小树枝对叶子都是一对多的关系，我们用圆圈代表树干和叶子，把自然界的树倒过来进行一次抽象，得下图（为了方便起见，我们的数据全为字符类型）：

可以看到，现实中的树完美契合我们需要的数据结构，所以我们称这种数据结构为树（Tree）。

7.1.1. 名词与概念

我们按图索骥，来认识树的相关名词。

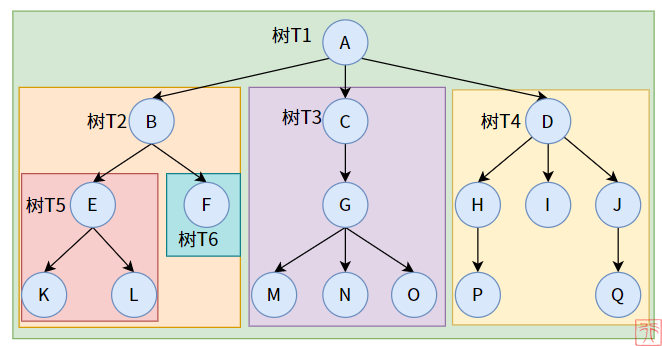
• 子树：树是一个有限集合，子树则是该集合的子集。就像套娃一样，一棵树下面还包含着其子树。

  比如，树T1 的子树为 树T2、T3、T4，树T2的子树为 T5、T6. 上图中还有许多子树没有标记出来。

• 结点（Node）：一个结点包括一个数据元素和若干指向其子树分支。

  比如，在树T1 中，结点A 包括一个数据元素A 和 三个指向其子树的分支。上图中共有 17 个结点。

• 根结点（Root）：一颗树只有一个树根，这是常识。在数据结构中，“树根”即根节点。

  比如，结点A 是树 T1 的根结点；结点C 是树T1 的子结点，是树 T3 的根结点。

• 度（Degree）：一个结点拥有的子树数。

  比如，结点A 的度为 3，结点G 的度为 3，结点H 的度为 1.

• 叶子（Leaf）/ 终端结点：度为 0 的结点被称为叶子结点，很形象吧。

  比如，对于树 T1来说，结点F、I、K、L、M、N、O、P、Q 均为叶子。

• 分支结点 / 非终端结点：和叶子结点相对，即度不为 0 的结点。

• 内部结点：顾名思义，在树内部的结点，即不是根结点和叶子结点的结点。

• 孩子（Child）、双亲（Parent）、兄弟（Sibling）、堂兄弟、祖先、子孙这些概念和族谱上的相同。

  比如，对于结点B 来说：结点A 是其双亲结点，结点E、F 是其孩子结点，结点C、D 是其兄弟结点，结点K 是其子孙结点。

• 层次（Level）：从根结点开始，根为第一层次，根的孩子为第二层次......以此类推。

  比如，结点K 在树 T1 中的层次为 4.

• 深度（Depth）/ 高度：指树的最大层次。

  比如，树 T1 的深度为 4.

• 有序树：如果结点的各子树从左到右是有次序的、不能颠倒，则为有序树，否则为无序树。对于有序树的孩子来说，最左边的孩子称为第一个孩子，最右边的孩子称为最后一个孩子。

  比如，如果树T1是一个有序树，则其根结点的第一个孩子为结点B，最后一个孩子为结点D.

7.1.2. 树的递归概念

前面已经介绍了树的轮廓和相关名词概念，为了回答什么是树这个问题，我们这里还需要介绍三种常见的树结构。

【空树】：一颗空树，即没有结点的树。

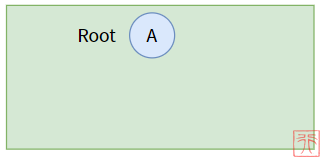
【只有根结点的树】：只有一个根节点，没有其他结点。

【普通的树】

现在我们能来回答什么是树了：

树（Tree）是由 N (N >= 0) 个结点构成的有限集合。

• 当 N = 0 时，树为空树
• 当 N = 1 时，树只有一个根结点
• 当 N > 1 时，树除了一个根结点外，其余结点又可分为若干个不相交的有限集合，我们称之为子树。

非空树有且仅有一个根结点。

树的一对多的关系存在于双亲结点和孩子结点之间。

在树中，因为存在树、子树的概念，所以树的子树仍是一颗树，子树的子树仍是一棵树。

举个例子：人类的孩子仍是人类，人类的孩子的孩子仍是人类。

因为存在双亲、孩子、子孙的概念，所以根结点的孩子结点可以其子树的根结点。

举个例子：一个人，在其孩子看来是父亲，在其父母看来是儿子。

这种概念，就是递归的概念。

即，对于某个“事物”而言，它的“孩子”和它本身并无实质区别，它做的事，它的“孩子”也会做、也要做。一直向下，“孙子”“曾孙”“玄孙”皆是如此。

为了说明递归这个概念，我们将上图的树递归地分解为子树，下图中每个区域都是一颗树（或子树）：

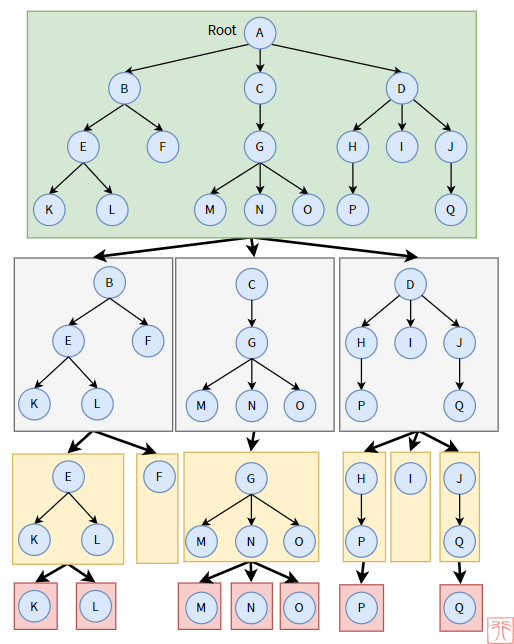
分解到最后，我们最终得到的，可以说是叶子结点，也可以说是只有根结点的树。如结点F、K、L.

在分解的过程中，我们还可以发现，对于每个结点来说，我们都可以将其看作某棵树（子树）的根结点。比如结点E、I都是某棵子树的根结点。这与树有且只有一个根结点并不矛盾。

这就好比我们说，小明只能有一个亲生父亲，但不影响他成为别人的父亲。

整个过程就像在族谱上从祖宗找到子孙一样。所以如果对树的概念有啥不了解的，可以找个族谱翻翻看。

到此，我们可以说，树的定义是一个递归的定义，树是由根结点和它的若干子树组成的，子树也是由根结点和它的若干子树组成的……即在树的定义中又用到树的定义。

7.1.3. 树和线性表的比较

看图直观体验何为（前驱结点和后继结点间）一对一的关系，何为（双亲结点和孩子结点之间）一对多的关系。

7.2. 初识二叉树

7.2.0. 什么是二叉树？

何为二叉树？首先它得是颗树，其次它得是二叉的。

前面已经初步认识了树，它的结点的孩子数量是没有限制的，即，你想要几个孩子就要几个孩子，想分几个叉就分几个叉。

而二叉树，则是限制了孩子数量，即每个结点最多只能有两个孩子（左孩子和右孩子），打个比方就是“二胎树”。

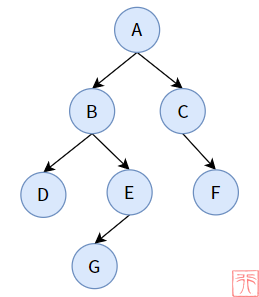
结点A 的左孩子是结点B，右孩子是结点C.

二叉树是一种每个结点至多有两棵子树（即每个结点的度最大为 2 ）的有序树。

7.2.1. 二叉树的几种形态

一、空二叉树

二、仅有根结点的二叉树

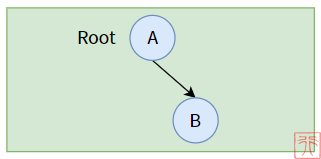
三、左子树为空的二叉树

四、右子树为空的二叉树

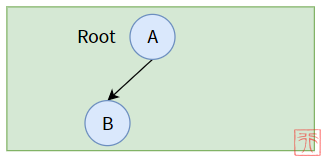
五、左右子树都不为空的二叉树

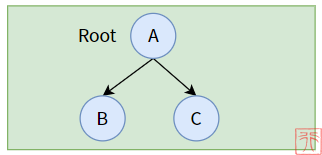
7.2.2. 满二叉树和完全二叉树

满二叉树的特点在于“满”，即每层的结点数都是最大结点数。

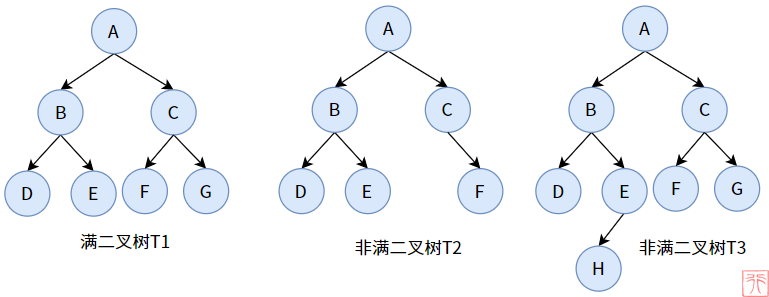
T2 的第 3 层次没有达到最大结点数，缺了 1 个；T3 的第 4 层次没有达到最大结点数，缺了 7 个。

完全二叉树是相对于满二叉树来说的，见下图：

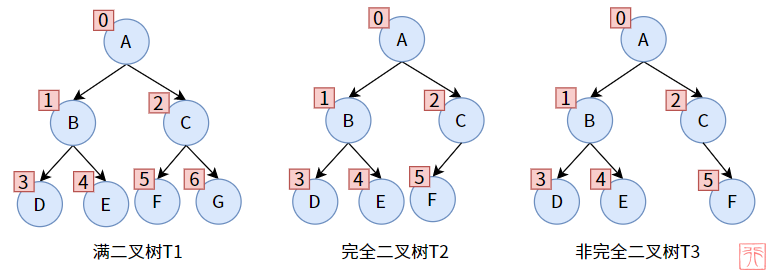
二叉树是有序树，对一颗满二叉树和一颗完全二叉树按「自上向下，自左向右」的顺序进行编号，如上图。

完全二叉树中的所有结点的编号必须和满二叉树的相同编号的结点在位置上完全相同。

换句话说，完全二叉树的结点按「自上向下，自左向右」的顺序不能中断。T3 的结点C 没有左孩子，显然按那个顺序是中断的。

7.3. 二叉树的遍历原理

本小节只讲述遍历的原理，具体代码实现在后面的小节中。

7.3.0. 如何遍历？

在线性表中，我们的遍历非常简单粗暴，找到线性表头，使用循环直接一股脑的到线性表尾，即完成遍历了。在树中，我们不能在做这么简单粗暴的事了，因为树是一对多的关系，所以从头到尾的遍历是不可能的。

遍历的实质是，利用循环将线性排列的元素顺序打印出来。（遍历操作不止干打印的事，为了方便起见，我们的遍历操作是打印元素）

而遍历和树之间的矛盾是，遍历是线性进行的，但我们的树不是线性的。

为了解决这个矛盾，我们可不可以约定好某种顺序，将树的元素按这种顺序线性排列起来，然后遍历就变成从头到尾的简单粗暴之事了？答案是可以的。

我们知道树是递归的定义，二叉树是由根结点、左子树、右子树这三部分递归地组合而成的。 所以我们要约定的就是这三部分谁先谁后。

按照人们写字先左后右的约定，我们也约定先左子树后右子树的顺序（当然你可以先右后左），那么根结点就只有三个位置可以放了。

• 根结点 >> 左子树 >> 右子树，称为先序（根）遍历
• 左子树 >> 根结点 >> 右子树，称为中序（根）遍历
• 左子树 >> 右子树 >> 根结点，称为后序（根）遍历

约定好之后，只需要按照顺序递归地来就好了，就像找族谱一样。

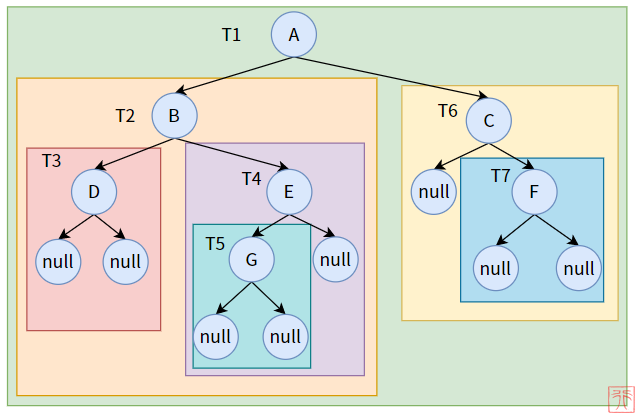
本节【7.3. 二叉树的遍历原理】以遍历下图中的二叉树为例：

为了方便起见，我们将 null 画出来，且将所有子树用颜色标志出来。

7.3.1. 先序遍历

先序遍历的递归描述如下：

若二叉树为空，则空操作；否则：

1. 访问根结点
2. 先序遍历左子树
3. 先序遍历右子树

你可能会问，怎么只有访问根结点这一步？左孩子和右孩子结点呢？前面说过一句话：对于每个结点来说，我们都可以将其看作某棵树（子树）的根结点。就像你的儿子会成为别人的父亲一样。所以只要递归地访问根结点，将每个结点递归地变为“根结点”，我们就能完成遍历。

所以与其说是在遍历结点，不如说是在遍历「根结点」，我们只是在递归地把“所有根结点”找出来而已。（因为每个结点都可以看做是根结点）

所以遍历的重点，在于将所有结点当作根结点看待。

又因为每棵树有且仅有一个根结点，所以我们要不断地递归分解子树（先左子树后右子树）。而只有正确地找到子树，我们才能将某个结点看作根结点。这样一直递归，直到分解到 NULL 为止。

举个例子，当我们认为结点 D 是根结点的时候，就意味着我们已经找到了树 T3，并且一定是针对 T3 而言的，否则就不能称结点 D为根结点。结点 D 只能是 T3 的根结点。

过程如下：

1. T1的根结点为结点A，输出A
2. T1的左子树不为空，为T2，进入T2
   1. T2的根结点为结点B，输出B
   2. T2的左子树不为空，为T3，进入T3
      1. T3的根结点为结点D，输出D
      2. T3的左子树为空，做空操作
      3. T3的右子树为空，做空操作
      4. 返回到T2
   3. T2的右子树不为空，为T4，进入T4
      1. T4的根结点为结点E，输出E
      2. T4的左子树不为空，为T5，进入T5
         1. T5的根结点为结点G，输出G
         2. T5的左子树为空，做空操作
         3. T5的右子树为空，做空操作
         4. 返回到T4
      3. T4的右子树为空，做空操作
      4. 返回到T2
   4. 返回到T1
3. T1的右子树不为空，为T6，进入T6
   1. T6的根结点为结点C，输出C
   2. T6的左子树为空，做空操作
   3. T6的右子树不为空，为T7，进入T7
      1. T7的根结点为结点F，输出F
      2. T7的左子树为空，做空操作
      3. T7的右子树为空，做空操作
      4. 返回到T6
   4. 返回到T1
4. 遍历完成

先序遍历的顺序为：A B D E G C F

如果你感觉文字描述不直观，可以在我以前写过的文章中找到二叉树遍历过程的动态图。

7.3.2. 中序遍历

中序遍历的递归描述如下：

若二叉树为空，则空操作；否则：

1. 中序遍历左子树
2. 访问根结点
3. 中序遍历右子树

过程如下：

1. T1的左子树不为空，为T2，进入T2
   1. T2的左子树不为空，为T3，进入T3
      1. T3的左子树为空，做空操作
      2. T3的根结点为结点D，输出D
      3. T3的右子树为空，做空操作
      4. 返回到T2
   2. T2的根结点为结点B，输出B
   3. T2的右子树不为空，为T4，进入T4
      1. T4的左子树不为空，为T5，进入T5
         1. T5的左子树为空，做空操作
         2. T5的根结点为结点G，输出G
         3. T5的右子树为空，做空操作
         4. 返回到T4
      2. T4的根结点为结点E，输出E
      3. T4的右子树为空，做空操作
      4. 返回到T2
   4. 返回到T1
2. T1的根结点为结点A，输出A
3. T1的右子树不为空，为T6，进入T6
   1. T6的左子树为空，做空操作
   2. T6的根结点为结点C，输出C
   3. T6的右子树不为空，为T7，进入T7
      1. T7的左子树为空，做空操作
      2. T7的根结点为结点F，输出F
      3. T7的右子树为空，做空操作
      4. 返回到T6
   4. 返回到T1
4. 遍历完成

中序遍历的顺序为：D B G E A C F

7.3.3. 后序遍历

后序遍历的递归描述如下：

若二叉树为空，则空操作；否则：

1. 后序遍历左子树
2. 后序遍历右子树
3. 访问根结点

过程和前序中序类似，不再描述，后序遍历的顺序为：D G E B F C A

7.3.4. 层序遍历

前面介绍了前序、中序和后序三种遍历方式，给人的直观感受是“不撞南墙（NULL 结点）不回头的愣头青”。

比如中序遍历，我们是“一头扎到底”地找左子树、左子树的左子树、左子树的左子树的左子树，直到找到 NULL 为止，才回头一步找右子树。

这个过程有点像我们在族谱上找自己那一支的祖宗：从老祖宗开始，只找自己的那一支的关系，父亲的兄弟姐妹、爷爷的兄弟姐妹皆不关心。

下面再介绍一种和以上三种皆不同的遍历——层序遍历。

树是有层次(见7.1.1. 名词与概念)的，从根结点开始，根为第一层次，根的孩子为第二层次......以此类推。层序遍历即按照这种层次来进行遍历。

这种有点像查族谱的时候，连带祖辈的兄弟姐妹也一块查。

层序遍历的顺序为：从上到下按层次遍历，同层次从左到右按顺序遍历。

如果说前序、中序、后序遍历偏向于“纵向”，那么我们可以说层序遍历偏向于“横向”。

所以上图树的层序遍历顺序为：ABCDEFG。

7.4. 二叉树的存储结构

7.4.0. 顺序存储——数组实现

前面介绍了满二叉树和完全二叉树，我们对其进行了编号——从 0 到 n 的不中断顺序编号，而恰好，数组也有一个这样的编号 —— 数组下标，只要我们把二者联合起来，数组就能存储二叉树了。

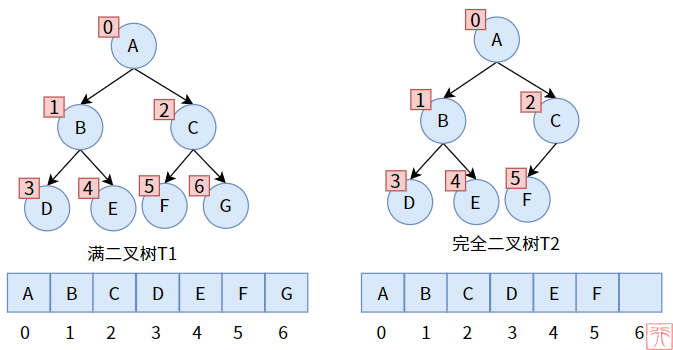
那么非满、非完全二叉树怎么使用数组存储呢？

我们可以在二叉树中补上一些虚构的结点，构造出来一个满/完全二叉树来，存储到数组中时，虚构的结点对应的数组元素不存储数据（# 代表虚构的不存在）。如下图：

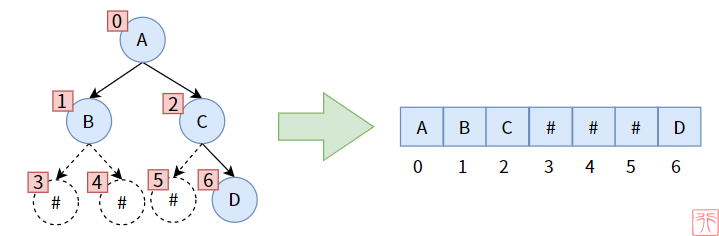
这样存储的缺点是，数组中可能会有大量空间未用到，造成浪费。

所以这种存储方式只适用于完全二叉树。

7.4.1. 链式存储——链表实现

我们画树的图时，采用的都是结点加箭头的方式，结点表示数据元素，箭头表示结点之间的关系，清晰明了。如果你对链表熟悉，那么肯定能觉察到这是典型的链式结构。链式结构完美解决了顺序结构中可能会浪费空间的缺点，而且也不会有数组空间限制。

下面来分析一下结点的结构。

树的结点包括一个数据元素和若干指向其子树分支。二叉树的结点则相对简单，包括：

• 数据元素
• 左子树分支（结点的左孩子）
• 右子树分支（结点的右孩子）

怎么来实现呢？单链表的结点是使用一个指向其后继结点的指针来表示其关系的。同样地，我们也可以使用指针来表示结点和其左孩子、右孩子的关系。

分析到这，二叉树的结点就清晰了：

• 一个存储数据的变量——data
• 一个指向其左孩子结点的指针——left_child
• 一个指向其右孩子结点的指针——right_child

上图中，叶子结点下的 NULL 结点是我们虚构出来的，便于理解。NULL 的作用是标识某个结点没有左子树或右子树，在实际实现时，只需将指针置空即可。

用 C 语言的结构体实现二叉树的结点（为了方便起见，我们的数据全为字符类型）：

/*二叉树的结点的结构体*/
typedef struct Node {
    char data; //数据域
    struct Node *left_child; //左孩子指针
    struct Node *right_child; //右孩子指针
} TreeNode;

7.5. 二叉树的创造

二叉树的定义是递归的定义，所以如果你想要创造一个二叉树，也可以借助递归去创造。如何递归创造呢？在现实中，一棵树先长根、再长枝干、最后长叶子。我们用代码创造树时，也遵守这个原则，即先创造根结点，然后左子树，最后右子树。整个过程和先序遍历相似。

我以前写过的某篇文章中有二叉树创建过程的动态图，这里不再赘述。

这里以创造下图中的树为例：

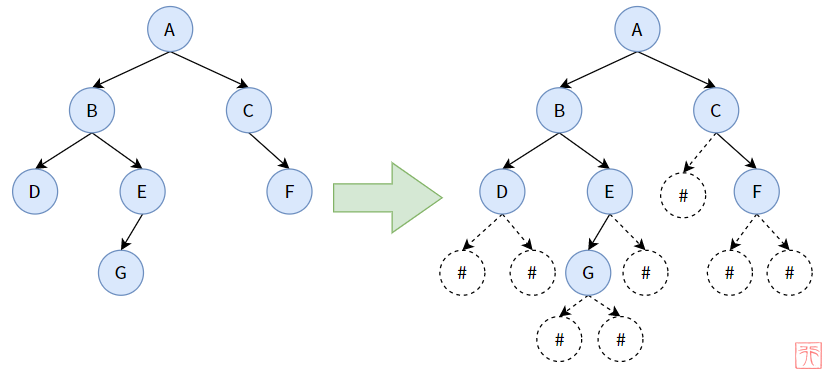
说明：当我们看到如左图的二叉树时，要立即能脑补出对应的右图。那么问题来了，#结点是什么？

在【7.3. 二叉树的遍历过程】和 【7.4.1. 链式存储——链表实现】中我们已经画出了类似的图，只不过那张图中出现的是 NULL 结点，它的作用是标识某个结点没有孩子，它是我们虚构出来的。

# 结点也是这个作用，只是因为我们在输入结点的时候无法直接输入 NULL 值，所以，在实际使用 C 语言创造二叉树时，需要使用 #或者其他的什么符号来告知程序这里应该是 NULL.

上图的先序遍历顺序为：ABDEGCF，如果加上 # 结点，则为：ABD##EG###C#F##. 我们就按照此顺序来创造二叉树。

代码如下：

/**
 * 创造一个二叉树
 * root: 指向根结点的指针的指针
 */
void create_binary_tree(TreeNode **root)
{
    char elem;
    scanf("%c", &elem);
    if (elem == '#') {
        *root = NULL;
    } else {
        *root = create_tree_node(elem); //创造一个二叉结点
        create_binary_tree(&((*root)->left_child));
        create_binary_tree(&((*root)->right_child));
    }
}

请注意，函数 create_binary_tree 接受的是一个指向根结点的指针的指针，至于为什么要使用指针的指针，理由在介绍单链表的时候——【2.6. 初始化链表】中已经解释了。

7.6. 二叉树的遍历实现

在 【7.3. 二叉树的遍历过程】中已经介绍了遍历的原理了，下面使用 C 语言实现它。

7.6.0. 遍历实质

这一点在【7.3.0. 如何遍历？】中已经介绍过，这里再提一下。

遍历的实质是将非线性的二叉树结点按照某种顺序给线性地排列起来，然后进行循环遍历。

按照什么顺序呢？

二叉树的定义是递归的定义，即在二叉树的定义中又用到了二叉树的定义。所以无论是在创造二叉树，还是在遍历二叉树，我们要做的只有三件事：访问根结点、找左子树、找右子树。所谓先序、中序、后序、层次遍历，无非是这三件事的顺序罢了。

顺序决定好了，二叉树从某种程度上就变成线性的了，我们就按照顺序线性遍历即可。

7.6.1. 先、中、后序遍历（递归实现）

我们如果使用递归代码，很容易就能实现遍历，而且代码非常简洁。

【先序遍历】

/**
 * 先序遍历
 * root: 指向根结点的指针
 */
void preorder_traversal(TreeNode *root)
{
    if (root == NULL) { //若二叉树为空，做空操作
        return;
    }
    printf("%c ", root->data); //访问根结点
    preorder_traversal(root->left_child); //递归遍历左子树
    preorder_traversal(root->right_child); //递归遍历右子树
}

【中序遍历】

/**
 * 中序遍历
 * root: 指向根结点的指针
 */
void inorder_traversal(TreeNode *root)
{
    if (root == NULL) { //若二叉树为空，做空操作
        return;
    }
    inorder_traversal(root->left_child); //递归遍历左子树
    printf("%c ", root->data); //访问根结点
    inorder_traversal(root->right_child); //递归遍历右子树
}

【后序遍历】

/**
 * 后序遍历
 * root: 指向根结点的指针
 */
void postorder_traversal(TreeNode *root)
{
    if (root == NULL) { //若二叉树为空，做空操作
        return;
    }
    postorder_traversal(root->left_child); //递归遍历左子树
    postorder_traversal(root->right_child); //递归遍历右子树
    printf("%c ", root->data); //访问根结点
}

事实上，大部分使用递归做的事，使用栈也可以做到。下面介绍遍历的栈实现。

7.6.2. 先、后序遍历（栈实现）

我们利用了栈的后进先出的特性，

栈实现的代码较复杂，受篇幅限制，这里只介绍先序遍历和后序遍历，详细代码请移步至代码仓库查看。

【先序遍历】

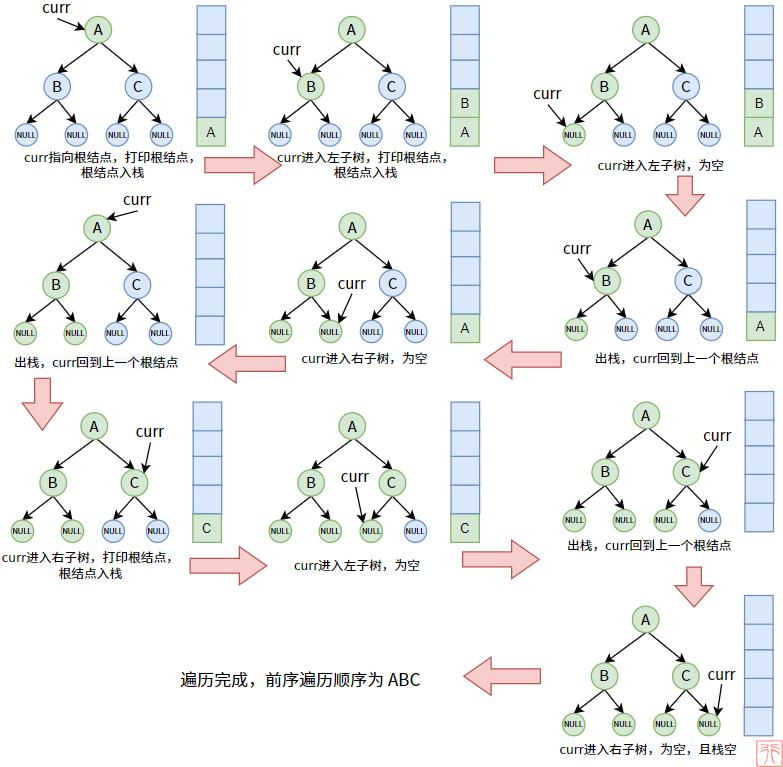
我们的树的结点是要全部都入栈的（暂不管顺序如何），那么入栈的条件是什么？就是该结点可以被看作某棵树（子树）的根结点的时候。即，curr 指针指向的结点一定为某颗树（子树）的根结点。

在 【7.3. 二叉树的遍历原理】中，我们已经看到了，遍历完某个子树时，一定要回到其双亲结点。这种回溯如何实现？可以利用栈的先进后出、后进先出的特点，这个特点能在栈种完美保存结点在树中父子关系，栈顶元素即为当前子树的双亲结点。

/**
 * 使用栈实现的先序遍历
 */
void preorder_traversal_by_stack(TreeNode *root)
{
    //创造并初始化栈
    Stack stack;
    init_stack(&stack);

    TreeNode *curr = root; //辅助指针curr

    while (curr != NULL || !stack_is_empty(&stack)) {
        while (curr != NULL) {
            printf("%c", curr->data); //打印根结点
            push(&stack, curr); //根结点入栈
            curr = curr->left_child; //进入左子树
        }
        if (!stack_is_empty(&stack)) {
            pop(&stack, &curr); //出栈，回到上一个根结点
            curr = curr->right_child; //进入右子树
        }
    }
}

【后序遍历】

后序遍历相较于前序和中序较为麻烦。因为先序和中序的根结点在右子树之前，所以我们可以在出栈的时候同时进行打印根结点和进入右子树。

后序遍历的根结点在右子树之后，这就要求我们再遍历完左子树后，先返回到根结点，然后进入右子树，遍历完右子树之后，再回到根结点，才能打印它。

关键之处还在于左子树、右子树、根结点的顺序。

所以当 curr 指针遍历完左子树后，我们不能直接将根结点出栈，而是先从栈顶读取到根结点，然后 curr 指针返回到根结点，然后 curr 指针进入右子树进行遍历，当右子树遍历完成后，将根结点出栈，才能打印根结点。

这样一来，后序遍历就有两次回到根结点的动作，且这两次的后续动作不一样。第一次通过读取栈顶回到根结点，然后进入右子树；第二次通过出栈回到根结点，然后打印根结点。

这样看似解决了后序遍历的顺序问题，但其实又得到了一个新的问题，即：我们如何知道右子树被遍历完了？

我们有两次回到根结点的动作，对于写代码的人来说，我们清楚知道两次回到根结点之后该干什么，知道右子树是否被遍历完了。但是对于 curr 指针来说，它不知道，两次回到根结点，它都不知道右子树是否被遍历完成了。

此时，对于curr 指针来说，就像有两条路摆在它面前让它选择其中一条，它难以抉择。但是如果当其中一条有过它的脚印，那么它就很容易选择那条没走过的路了。

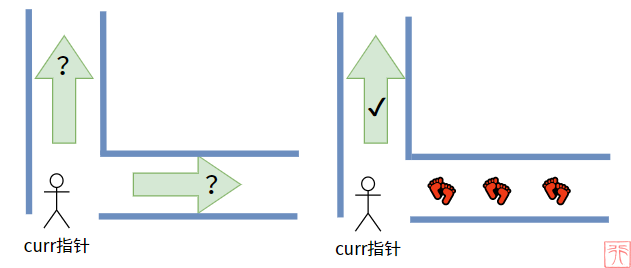
所以我们现在还需要一个“脚印”指针——prev，prev指针用来记录 curr访问过的结点。

当 curr 指针第二次回到根结点的时候，一看，哦！我的脚印留在那呢！（prev 指针指在右子树那里）curr 指针就直接放心打印根结点了。

/**
 * 使用栈实现的后序遍历
 */
void postorder_traversal_by_stack(TreeNode *root)
{
    Stack stack;
    init_stack(&stack);

    TreeNode *curr = root; //辅助指针curr，记录当前访问结点
    TreeNode *prev = NULL; //脚印指针prev，记录上一个访问过的结点

    while (curr != NULL || !stack_is_empty(&stack)) {
        if (curr != NULL) {
            push(&stack, curr); //根结点入栈
            curr = curr->left_child; //进入左子树
        } else {
            get_top(&stack, &curr); //读栈顶元素，不是出栈
            //右子树不为空，且右子树没被遍历
            if (curr->right_child != NULL && curr->right_child != prev) { 
                curr = curr->right_child; //进入右子树
                push(&stack, curr); //根结点入栈
                curr = curr->left_child; //进入左子树
            } else { //右子树已被遍历或者右子树为空，可以打印根结点了
                pop(&stack, &curr); //根结点出栈
                printf("%c", curr->data); //打印根结点
                prev = curr; //记录
                curr = NULL; //置空，进入下一轮循环
            }
        }
    }
}

7.6.3. 层序遍历（队列实现）

我们思考几个问题。

问 ：先序、中序、后序遍历是如何找到左子树的？

答 ：通过根结点进入左子树的。

问 ：先序、中序、后序遍历是如何找到右子树的？

答 ：左子树为空，先返回根结点，然后通过根结点进入右子树的。

问 ：要想找到子树，必须通过谁？

答 ：根结点。

在【7.3.4. 层序遍历】中已经比较了先、中、后序和层序的不同。

先、中、后序遍历偏向于“纵向”遍历，即找孩子、孩子的孩子、孩子的孩子的孩子......

层序遍历则偏向于“横向”遍历，即找孩子、孩子的兄弟们、孩子的孩子的兄弟们......

为什么层序遍历的思路有所不同呢？

一、我们是按层次进行逐层遍历的。这就要求我们找到根结点后，要能够找到其所有孩子。先序遍历那样的方式已经行不通了，因为孩子们的唯一共同点就是拥有同一个双亲，我们不同通过某一个孩子找到它的兄弟。只能在找到根结点的时候同时找到其所有孩子。

二、同层次的遍历是按照从左到右的顺序进行的。这就要求我们在通过根结点找到其所有孩子时，要保存孩子们之间的顺序。

如何做？可以借助其他数据结构，我们已经介绍了两种可以保存顺序的数据结构——栈和队列。

栈的入栈顺序和出栈顺序时相反的，队列的入队顺序和出队顺序则是相同的，所以我们选择队列。

具体遍历如下图：

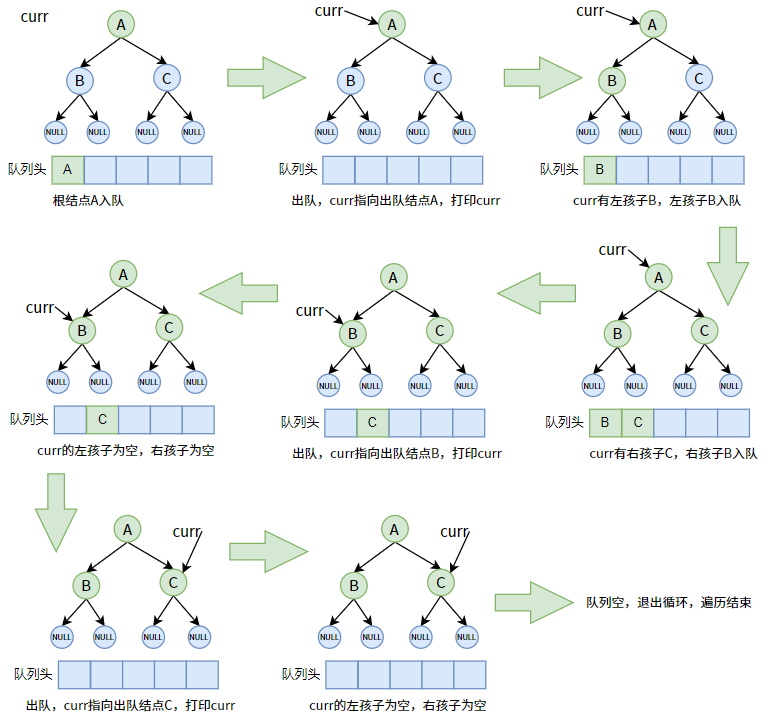
可见，队列的作用是存储结点的层序关系。

找到根结点（第 1 层次），将根结点和其所有孩子（第 2 层次）按顺序入队：A、B、C，这样一来，出队顺序就是层序遍历的顺序。如果结点B、C还有孩子（第 3 层次），那么我们在结点B、C出队的时候，将它们的所有孩子按顺序入队即可，这样一来，第 2 层次的结点出队完（遍历完）后，就能按顺序继续出队（遍历）第 3 层次的结点。

代码实现如下：

/**
 * 使用队列实现层序遍历
 */
void levelorder_travelsal_by_queue(TreeNode *root)
{
    Queue queue;
    TreeNode *curr;
    init_queue(&queue); //初始化队列

    en_queue(&queue, root); //入队

    while (!queue_is_empty(&queue)) {
        de_queue(&queue, &curr); //出队
        printf("%c", curr->data);
        if (curr->left_child != NULL) { //如果左孩子不为空
            en_queue(&queue, curr->left_child); //左孩子入队
        }
        if (curr->right_child != NULL) { //如果右孩子不为空
            en_queue(&queue, curr->right_child); //右孩子入队
        }
    }
}

以上代码中，栈和队列的相关函数这里不再给出，详细代码请移步至代码仓库。

7.6.4. 总结

到此为止，我们讲了四种遍历方式：先序、中序、后序、层序遍历，是时候总结一下了。

我们在遍历二叉树的时候，重点是将所有结点按照某种顺序给线性排列起来。因为二叉树是非线性的结构，而遍历操作是对于线性序列而言，使用循环完成的（你可以去看一看链表、栈、队列等线性表的遍历）。

但看递归实现的遍历，我们还不好理解那句“将所有结点按照某种顺序给线性排列起来”，但如果把目光放到栈实现和队列实现的遍历上的话，这句话就很好理解了。

先序、中序和后序遍历的特点是“纵向”的，我们称这种遍历为深度优先遍历。

套路是：通过根结点找到左子树，然后借助递归或者栈，将根结点存储起来，等左子树遍历完之后，将存储的根结点拿出来，再通过它找到右子树，然后遍历右子树。按照此规则遍历所有子树。

层序遍历的特点是“横向”的，我们称这种遍历为广度优先遍历。

套路是：找到根结点，将该根节点的所有孩子入队列，然后边出队列边把出队元素的孩子入队。借助队列把每层的结点之间的关系存储起来，以实现层序遍历。

7.7. 线索二叉树

7.7.0. 为什么要用到线索二叉树？

我们先来看看普通的二叉树有什么缺点。下面是一个普通二叉树（链式存储方式）：

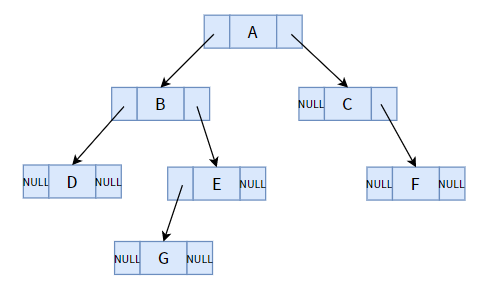
乍一看，会不会有一种违和感？整个结构一共有 7 个结点，总共 14 个指针域，其中却有 8 个指针域都是空的。对于一颗有 n 个结点的二叉树而言，总共会有 n+1 个空指针域，这个规律使用所有的二叉树。

这么多的空指针域是不是显得很浪费？我们学习数据结构和算法的重点就是在想法设法地提高时间效率和空间利用率。这么多的指针域就这么白白浪费了，太败家了！

所以我们要想法子好好利用它们，利用它们来帮助我们更好地使用二叉树这个数据结构。

那么如何利用呢？

前面已经强调过很多次了，遍历二叉树的实质是将二叉树中非线性结构的结点转化为线性的序列，然后才能方便我们遍历。

比如上图的中序遍历序列为：DBGEACF。

对于一个线性序列（线性表）来说，它有直接前驱和直接后继的概念（在【1.0. 什么是线性表？】中介绍过）。比如在中序遍历序列中，B 的直接前驱为 D，直接后继为 G。

我们之所以能知道 B 的直接前驱和直接后继，是因为我们按照中序遍历的算法，把二叉树的中序遍历序列写出来了，然后根据这个顺序序列说谁的前驱是谁、后继是谁。

直接前驱和直接后继是不能完全直接通过二叉树得到的，因为二叉树中只有双亲和孩子结点之间的直接关系，即二叉树的结点指针域中只存储了其孩子结点的地址。

现在的需求是，我想能直接从二叉树上得到某结点在中序遍历方式下的直接前驱和直接后继。

这时候就需要用到线索二叉树了。

7.7.1. 什么是线索二叉树？

当然，我们肯定需要借助结点的指针域来保存直接前驱和直接后继的地址。

其实，在上图的普通二叉树中（以中序遍历得到的序列），部分结点（指针域不为空的结点）是可以找到其直接前驱或后继的，比如结点 E 的左孩子 G 就是结点 E 的直接前驱；结点 A 的右孩子 C 就是结点 A 的直接后继。

但部分结点（指针域为空）是行不通的，比如结点 G 的直接后继是 E，直接前驱是 B，但在二叉树中却不能得出这样的结论。怎么办呢？我们注意到，结点 G 的两个指针域都为 NULL，并未被利用，那么我们使用这两个指针，分别指向其前驱和后继不就好了吗？

实在是两全其美，天作之合！但是问题并没有解决！

因为我们是利用空指针域来指向前驱或后继的，对于那些指针域不为空的结点，这样是矛盾的，比如结点 E 和结点 B。

既然有矛盾，那么我们就发现产生矛盾的根源，解决矛盾。

产生矛盾的根源是：结点的指针域为空和不为空时，指针的指向矛盾。即，指针不为空时指向孩子和指针为空时指向前驱或后继之间的矛盾。

那么我们对症下药，把指针域为空和不为空给区分出来，清晰地告诉指针：不为空时指向孩子，为空时指向前驱或后继。这就需要我们给两个指针各添加一个标志位。

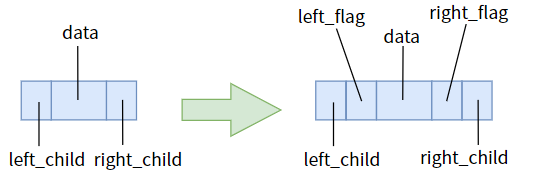
并约定以下规则：

• left_flag == 0 时，指针 left_child 指向左孩子
• left_flag == 1 时，指针 left_child 指向直接前驱
• right_flag == 0 时，指针 right_child 指向右孩子
• right_flag == 1 时，指针 right_child 指向直接前驱

二叉树的结点要有所变化：

/*线索二叉树的结点的结构体*/
typedef struct Node {
    char data; //数据域
    struct Node *left_child; //左指针域
    int left_flag; //左指针标志位
    struct Node *right_child; //右指针域
    int right_flag; //右指针标志位
} TTreeNode;

有了标志位，一切就能理清了。我们称指向直接前驱和后继的指针为线索。标志位为 0 的指针是指向孩子的指针，标志位为 1 的指针是线索。

一个二叉链表树，结点结构如上，我们将所有空指针都变为线索，这样的二叉树就是二叉线索树。

7.7.2. 如何创造线索二叉树？

在普通二叉树中，我们想要获取某个结点在某种遍历次序下的直接前驱或后继，每次都需要遍历获取到遍历次序之后才能知道。而在线索二叉树中，我们只需要遍历一次（创造线索二叉树时的遍历），之后，线索二叉树就能“记住”每个结点的直接前驱和后继了，以后都不需要再通过遍历次序获取前驱或后继了。

我们按照某种遍历方式，把普通二叉树变为线索二叉树的过程被称为二叉树的线索化。

接下来，我们用中序遍历的方式，将下面的二叉树线索化为线索二叉树

将标志位为 1 的指针，按照中序遍历序列，使其指向前驱或后继：

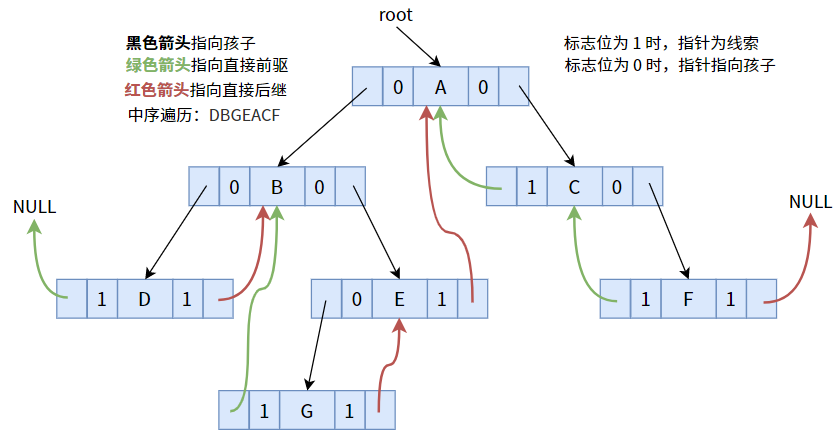
其中，结点 D 没有直接前驱，结点 F 没有直接后继，故指针为 NULL。

到此，我们算是解决了拥有 n 个结点的二叉树存在 n+1 个空指针域所造成的浪费，解决方式是给每个结点的指针增加一个标志位，以此来利用空指针域。标志位中存储的是 0 或 1 的布尔值，与浪费的空指针域相比，是相对比较划算的。而且使二叉树具有了一种新特性——二叉树中能保存在某种遍历次序下的结点之间的前驱和后继关系。

7.7.3. 线索化的实现

请注意一点，线索二叉树是由普通二叉树得来的，而且是按某种遍历顺序得来的。因为线索是在知道某个结点的前驱和后继的情况下才能设置，而前驱和后继关系不能通过二叉树直接体现，只能通过遍历二叉树得到的线性序列得出关系。所以要通过某种遍历方式得到具有前驱和后继关系的序列后，才能修改结点的空指针，进而设置线索。

即：线索化的实质是在按照某种遍历次序进行遍历二叉树的过程中修改结点的空指针，使其指向其在该遍历次序下的直接前驱或直接后继的过程。

我们在【7.3. 二叉树的遍历原理】和【7.6. 二叉树的遍历实现】分别介绍了二叉树四种遍历方式的原理及代码实现。当时我们是以打印为例来介绍遍历的。但遍历不止做打印的事，还可以做线索化的事。

所以，代码的大体结构还是一样的，我们只需把遍历代码中的打印代码换成线索化的代码，并作出一些其他改变即可。

下面以下图为例，分别介绍三种线索化：

一颗未线索化的二叉树，其所有标志位均默认为 0.

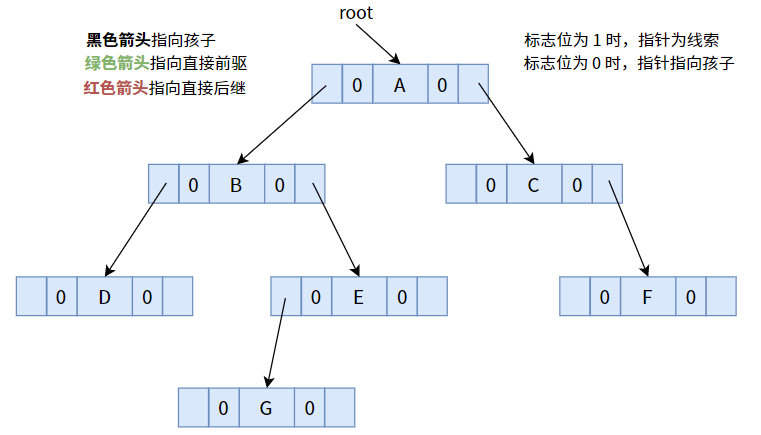
7.7.3.0. 中序线索化

按照中序遍历次序线索化后，可得下图：

我们先再次明确以下内容：

• 我们是在遍历二叉树的过程中进行线索化的。

• 中序遍历的顺序为：左子树 >> 根 >> 右子树。

• 线索化修改两个东西：空指针域和其对应的标志位。

• 如何修改？将空指针域置为直接前驱或后继。

所以我们的问题变成了：

1. 找到所有空指针域。
2. 找到空指针域所属结点，在先序次序下的直接前驱和直接后继。
3. 修改空指针域的内容，及其标志位，使该指针称为线索。

说明：我们在遍历二叉树时，使用到了递归，所以在进行线索化的时候，也会使用它。

具体代码如下：

//全局变量 prev 指针，指向刚访问过的结点
TTreeNode *prev = NULL;

/**
 * 中序线索化
 */
void inorder_threading(TTreeNode *root)
{
    if (root == NULL) { //若二叉树为空，做空操作
        return;
    }
    inorder_threading(root->left_child);
    if (root->left_child == NULL) {
        root->left_flag = 1;
        root->left_child = prev;
    }
    if (prev != NULL && prev->right_child == NULL) {
        prev->right_flag = 1;
        prev->right_child = root;
    }
    prev = root;
    inorder_threading(root->right_child);
}

7.7.3.0. 先序线索化

按照先序顺序线索化后，可得下图：

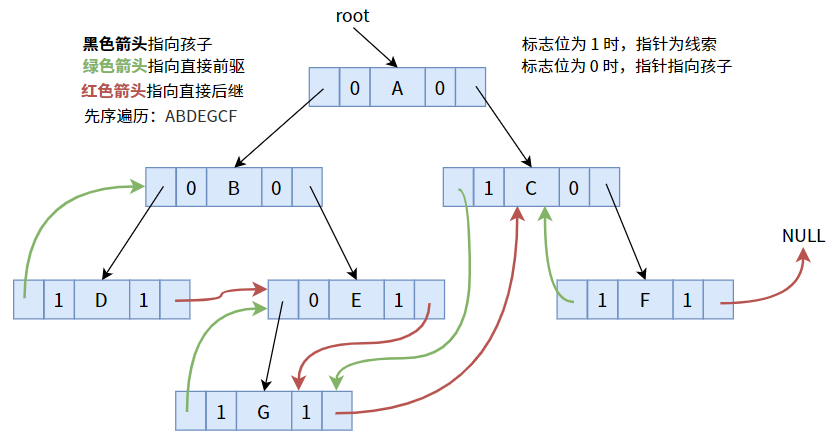
具体代码如下：

// 全局变量 prev 指针，指向刚访问过的结点
TTreeNode *prev = NULL;

/**
 * 先序线索化
 */
void preorder_threading(TTreeNode *root)
{
    if (root == NULL) {
        return;
    }
    if (root->left_child == NULL) {
        root->left_flag = 1;
        root->left_child = prev;
    }
    if (prev != NULL && prev->right_child == NULL) {
        prev->right_flag = 1;
        prev->right_child = root;
    }
    prev = root;
    if (root->left_flag == 0) {
        preorder_threading(root->left_child);
    }
    if (root->right_flag == 0) {
        preorder_threading(root->right_child);
    }
}

7.7.3.2. 后序线索化

按照后序遍历次序线索化后，可得下图：

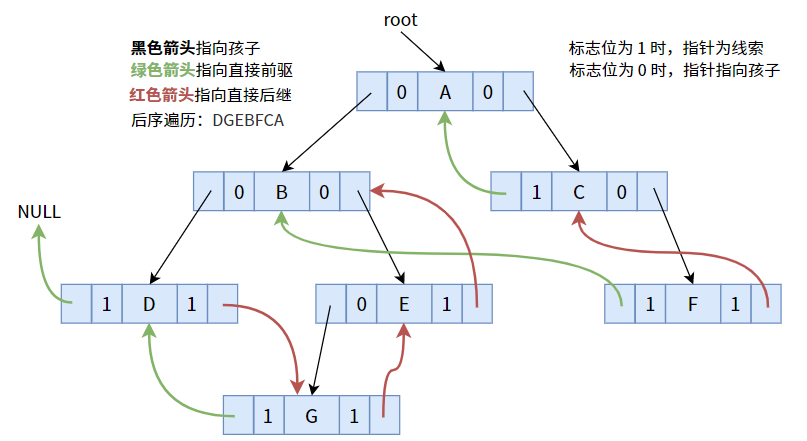
具体代码如下：

//全局变量 prev 指针，指向刚访问过的结点
TTreeNode *prev = NULL;

/**
 * 后序线索化
 */
void postorder_threading(TTreeNode *root)
{
    if (root == NULL) {
        return;
    }
    postorder_threading(root->left_child);
    postorder_threading(root->right_child);
    if (root->left_child == NULL) {
        root->left_flag = 1;
        root->left_child = prev;
    }
    if (prev != NULL && prev->right_child == NULL) {
        prev->right_flag = 1;
        prev->right_child = root;
    }
    prev = root;
}

线索二叉树充分利用了二叉树中的空指针域，给予二叉树一个新特性——通过一次遍历进行线索化后，二叉树中就能保存其结点之间的前驱和后继关系。

所以，如果我们需要频繁遍历二叉树，查找某个结点的直接前驱或后继结点，使用线索二叉树是非常合适的。

7.8. 二叉堆

7.8.0. 什么是二叉堆？

“二叉”自不必多说，本章主要介绍的树都是二叉树。那么啥是“堆”呢？

我们在日常生活中，通常会说“一堆东西”或者“堆东西”，这里的“堆”，通常指重叠放置的许多东西。

我们在堆东西的时候，肯定都有一个经验，即：为了使这堆东西更稳定，会将比较重的、大的东西放在下面，比较轻的、小的东西放在上面。

这个经验放在数据结构——二叉树中，同样适用。只不过“重”“大”是根据结点值的大小来判断的，并且是在双亲结点和孩子结点之间进行比较的。

比如，结点值大的，作为孩子结点；结点值小的，作为双亲结点。

下面举一个例子，先看下面一颗普通二叉树，也是一颗完全二叉树：

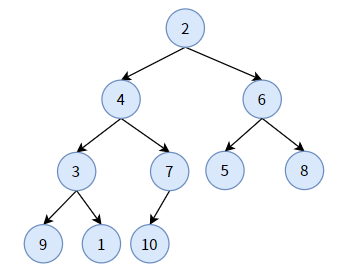
再看下面一颗二叉堆：

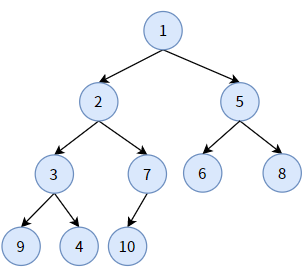
这个二叉堆的特点是：

• 它是一颗完全二叉树。事实上，该二叉堆就是由上图的完全二叉树经过调整转化而来；
• 任何一个双亲结点的值，均小于或等于左孩子和右孩子的值；
• 每条分支从根结点开始都是升序排序（如分支 1-2-3-4）。

这样的二叉堆被称为最小堆，它的堆顶，即根结点 A，是整棵树的最小值。

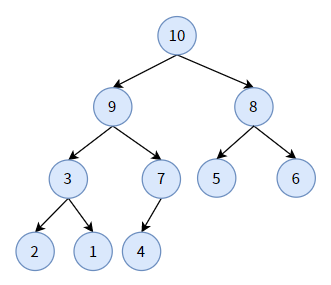
与最小堆相对应的是最大堆：

• 最大堆是一颗完全二叉树；
• 它的任何一个双亲结点的值，均大于或等于左孩子和右孩子的值；
• 每条分支从根结点开始都是降序排序。

最大堆的堆顶，是整棵树的最大值。

我们将上图中的普通二叉树转化为最大堆，如下图：

7.8.1. 二叉堆的操作

7.8.1.0. 构造二叉堆

给你一颗完全二叉树，如何调整结点，构造出一个二叉堆？下面是一颗无序的完全二叉树：

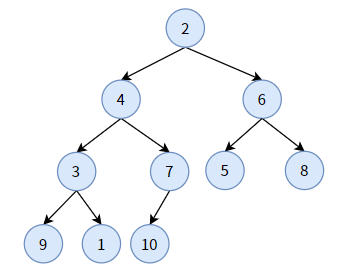
现在我们想要构造出一个最小堆，首先找到这颗完全二叉树中所有的非叶子结点（绿色标记）：

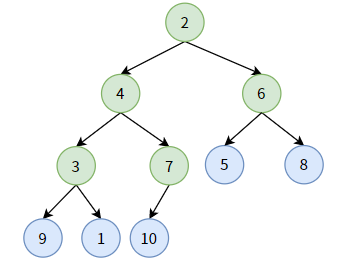
我们要做的事是：对每个非叶子结点，做最小堆的“下沉”调整。

何谓最小堆的“下沉”调整？

对某个非叶子结点，如果该结点大于其孩子结点中最小的那个，则交换二者位置，否则不用交换。在图上则表现出非叶子结点（即大值结点）“下沉”一个层次。运动是相对的，大值结点“下沉”，就相当于小值结点“上浮”。

需要注意的是，有时下沉一次是不够的，我们需要下沉多次，确保该结点下沉到底（即它不再大于其孩子）。

所有非叶子结点，从最后一个开始，按照从右到左，从下到上的顺序进行多次最小堆的下沉调整，即可构造成最小堆。

比如对于值为 4 的非叶子结点而言，它下沉到第 3 层次后，仍然大于其孩子，这不算“下沉到底”，还需要继续下沉到第 4 层次。至此，在分支 2-4-3-1 上，“大值”结点 4 算是下沉到底了。

下面进行分步解释：

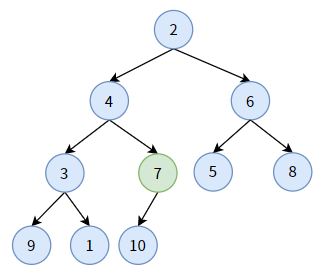
1. 对非叶子结点 7，它小于其孩子结点 10， 不用“下沉”；

   

2. 对非叶子结点 3，它大于其孩子结点中较大的结点 1，结点 3 要“下沉”，和结点 1 交换。显然，结点 3 沉到底了。

   

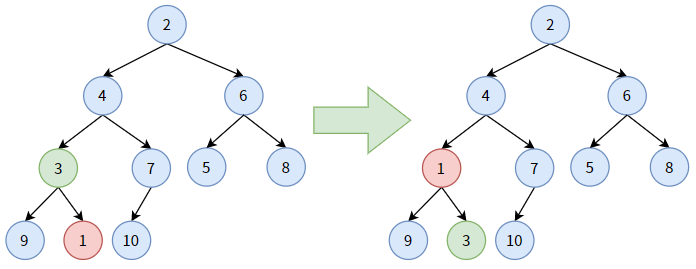
3. 对非叶子结点 6，它大于其孩子结点中较小的结点 5，结点 6 要“下沉”， 和结点 5 交换位置。显然，结点 6 沉到底了。

   

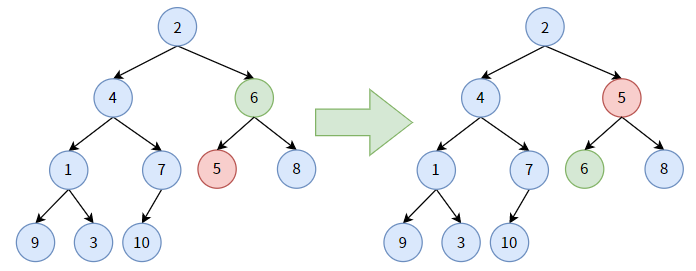
4. 对非叶子结点 4，它大于其孩子结点中最小的结点 1，结点 4 要 “下沉”，和结点 1 交换位置。显然，结点 4 并未沉到底。

   

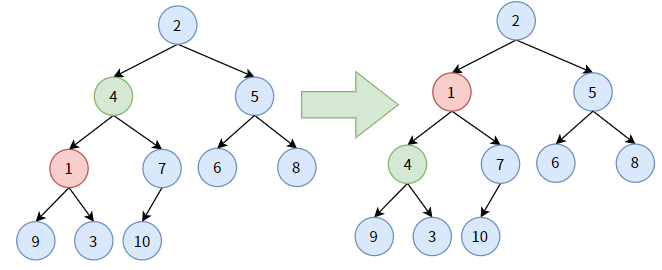
5. 仍对结点 4，它大于其孩子结点中最小的结点 3，结点 4 要“下沉”， 和结点 3 交换位置。此时，结点 4 算是沉底了。

   

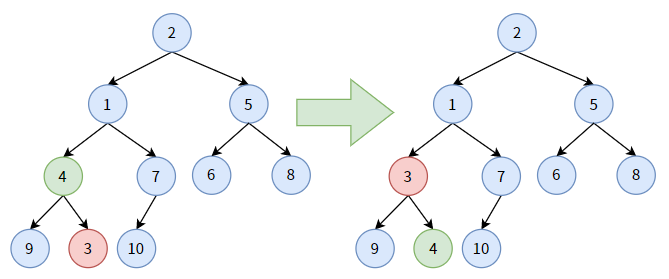
6. 对非叶子结点 2，它大于其孩子结点中最小的结点 1，结点 2 要“下沉”，和结点 1 交换位置。显然，结点 2 算是沉到底了。

   

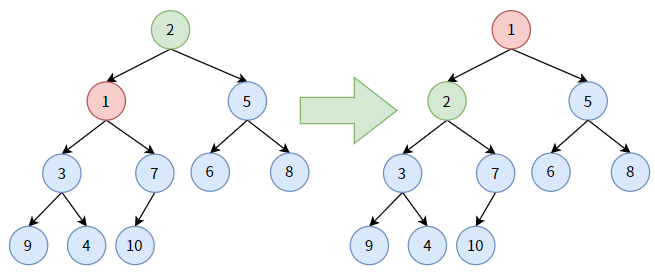
至此，我们将一颗无序的完全二叉树调整改造成了最小二叉堆，你可以检查一下，最小堆中的所有结点皆满足双亲的值小于孩子的值。并且，5 条分支上都是有序的。

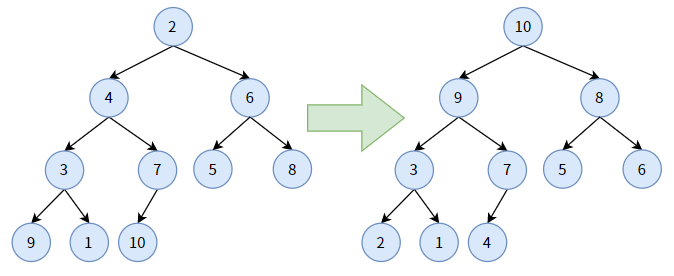
构造最大堆的步骤类似，不过最大堆的下沉调整是：如果某结点小于其孩子结点中最大的那个，则交换二者位置，在图上表现为非叶子结点（即小值结点）“下沉”一个层次。通过多次下沉调整，使该结点不再小于其孩子。

下图把一个无序完全二叉树调成为最大堆：

7.8.1.1. 插入结点

二叉堆是一个完全二叉树，要向其中插入结点，插入到完全二叉树的最后一个结点的下一个位置即可。

比如向下面的一个最大堆中插入结点 11，要插到最后一个结点 4 的下一个位置。当最大堆新插入一个结点 11 时，它就不再是最大堆了，因为结点 11 破坏了原堆的结构。所以，我们应当将其看作一个新的完全二叉树，然后调整新完全二叉树再次构造出最大堆。（调整过程见上）

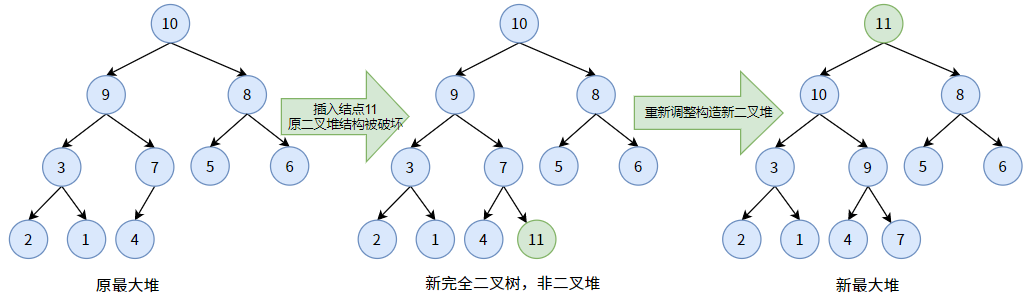
7.8.1.2. 删除结点

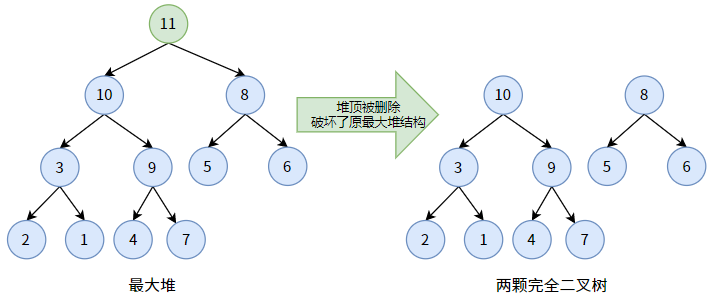
删除操作与插入操作相反，是删除第一个位置的元素，即删除堆顶。

我们以删除上图最大堆的堆顶 11 为例。

当删除堆顶 11 后，二叉堆原结构被破坏，甚至不是一颗二叉树了（变成两颗）：

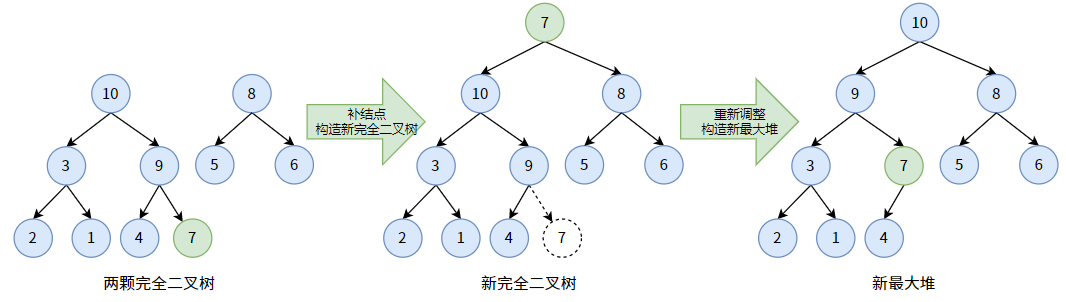
为了保持完全二叉树的形态，我们把最后一个结点 7 补到根结点去，顶替被删除的根结点 11。如此一来，我们又得到了一个新完全二叉树（不是二叉堆），然后我们根据这颗新完全二叉树再次构造出最大堆即可。

总结一下：

构造最大堆的本质是：将每颗子树的“大”结点上浮作为双亲，“小”结点下沉作为孩子。

构造最小堆的本质是：将每颗子树的“小”结点上浮作为双亲，“大”结点下沉作为孩子。

插入结点的本质是：插入新结点至二叉堆末尾，破坏了原二叉堆的结构，然后调整新得到的完全二叉树，重新构造二叉堆。

删除结点的本质是：删除堆顶，破坏了原完全二叉树的结构，然后使用最后一个结点，重新构造完全二叉树，再调整新得到的完全二叉树，重新构造二叉堆。

用四个字概括就是——破而后立。

7.8.2. 二叉堆的存储结构

二叉堆的存储结构是顺序存储，因为二叉堆是一颗完全二叉树，在【7.4.0. 顺序存储——数组实现】中我们说过：完全二叉树适合使用顺序存储结构来实现。

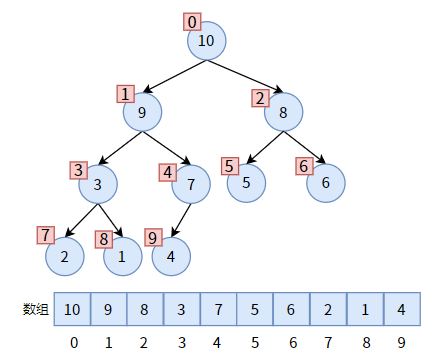
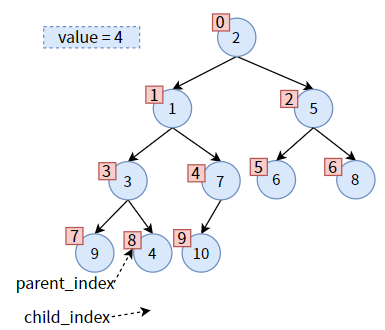
下图是一个最大堆，红色方框是对结点的编号，和数组下标一一对应。

链式存储结构能够清晰而形象地为我们展现出二叉堆中双亲结点和左右孩子的关系。但是数组中没有指针，只有数组下标，怎么表示双亲和孩子的关系呢？

其实对于完全二叉树来说，数组下标足矣！

现假设二叉堆中双亲结点的数组下标为 parent_index，左孩子的数组下标为 left_child_index，右孩子的数组下标为 right_child_index，那么它们之间有如下关系：

（一）left_child_index = 2 × parent_index + 1

（二）right_child_index = 2 × parent_index + 2

（三）parent_index = (left_child_index - 1) ÷ 2

（四）parent_index = (right_child_index - 2) ÷ 2

（五）right_child_index = left_child_index + 1

比如：结点 3 的下标为 3 ，则其左孩子 2 的下标为 2 × 3 + 1 = 7、右孩子 1 的下标为 2 × 3 + 2 = 8；

结点 3 的下标为 3，作为左孩子，其双亲下标为 (3 - 1) ÷ 2 = 1；结点 7 的下标为 4，作为右孩子，其双亲下标为 (4 - 2) ÷ 2 = 1；

假设某结点的数组下标为 child_index，你不知道该结点是左孩子还是右孩子，要求其双亲的下标，有

（六）parent_index = (child_index - 1) ÷ 2

比如：你不知道结点 5（下标为 5）、结点 6（下标为 6）是左孩子还是右孩子，则结点 5 和结点 6 的双亲下标分别为 (5 - 1) ÷ 2 = 2 、(6 - 1) ÷ 2 = 2。（注意，编程语言中的整型运算，所以结果不是小数）

这里，我们使用结构体实现二叉堆：

#define MAXSIZE 20 // 数组的最大存储空间

typedef struct {
    int array[MAXSIZE]; // 存储数组
    int length; // 当前堆长度（结点数）
} BinaryHeap;

在进行实际操作之前，需要初始化二叉堆，即对数组及堆长度赋值：

/**
 * @description: 初始化二叉堆
 * @param {BinaryHeap} *heap 二叉堆
 * @param {int} *array 数组首地址，该数组是一个无序完全二叉树
 * @param {int} arr_length 数组长度
 * @return {*} 无
 */
void init_heap(BinaryHeap *heap, int *array, int arr_length)
{
    // array 拷贝到 heap 中
    memcpy(heap->array, array, arr_length * sizeof(int));
    // 设置堆长度
    heap->length = arr_length;
}

7.8.3. 二叉堆的具体实现

7.8.3.0. 调整和构造

这里以构造最小堆为例。

要构造一个最小堆，就得调整所有的非叶子结点。而调整的依据就是比较非叶子结点和其孩子的大小。

我们约定 parent 为非叶子结点， parent_index 为其下标。child 为其孩子中较小的那个，child_index为其下标。

child 开始默认标识左孩子，那么右孩子的下标即为 child_index + 1。当左孩子小于等于右孩子时，child 不需要改变；当左孩子大于右孩子时，就得更新 child_index ，使child 标识右孩子。

下面结合下图中值为 4 的非叶子结点为例，讲述代码如何实现。

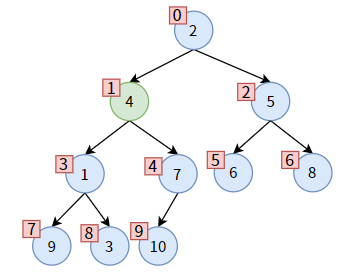
先比较 parent 的左右孩子，左孩子较小，则 child 为左孩子，不需要更新 child_index。

parent 和 child 各就各位，发现 parent 大于 child，可以交换位置。在交换之前，先保存一下 parent 的值，即 parent_value = 4：

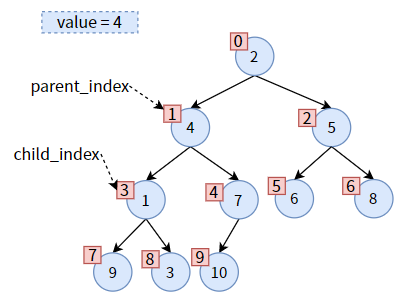
交换位置：先把 child的值赋给 parent，从而达到 值1 上浮的效果：

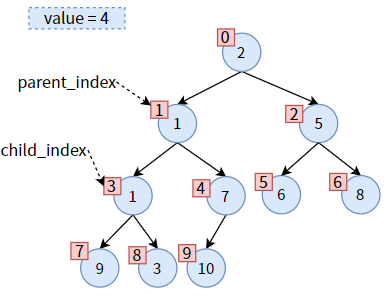
然后更新 parent_index 和 child_index，二者都往下走一层次：

然后将之前保存的 value 赋给现在的 parent，从而达到 值4 下沉的效果：

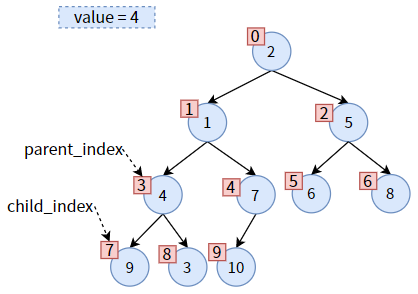
一次调整完成，但对于 值4 来说，并没有结束，因为 值4 还没有沉到底。

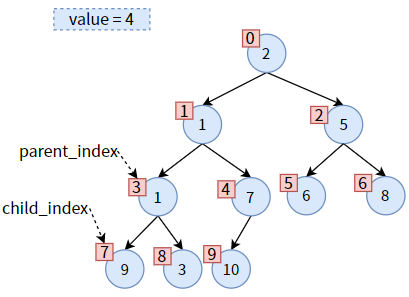
比较此时 parent 的左右孩子，发现右孩子较小，则 child 为右子树，需要更新 child_index，使 child 标识右孩子：

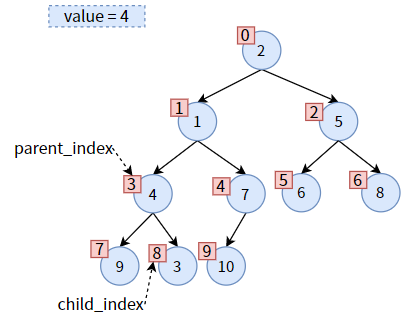
现在可以交换位置了，把 child 的值赋给 parent，达到 值3 的上浮：

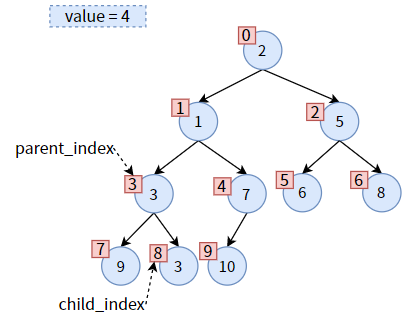
然后，更新 parent_index 和 child_index 的值，二者向下走一个层次：

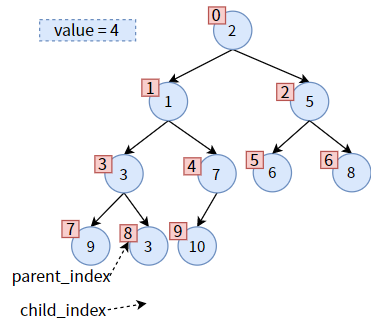
把 value 赋给 parent，达到 值4 的下沉：

此时，child_index 已超过了二叉堆的长度，即 值4 已经到底了。

调整代码如下：

/**
 * @description: 针对某个非叶子结点进行到底的下沉调整
 * @param {BinaryHeap} *heap 二叉堆（无序）
 * @param {int} parent_index 某个非叶子结点
 * @return {*} 无
 */
void adjust_for_min_heap(BinaryHeap *heap, int parent_index)
{
    // value 保存非叶子结点的值
    int value = heap->array[parent_index];
    // child_index 标识左孩子
    int child_index = parent_index * 2 + 1;
    // 最后一个结点的下标
    int last_child_index = heap->length - 1;

    // 双亲结点 parent 至少有一个孩子
    while (child_index <= last_child_index) {
        // 如果双亲结点 parent 有左孩子和右孩子
        if (child_index < last_child_index) {
            // 比较左孩子和右孩子谁小，如果右孩子小，
            if (heap->array[child_index] > heap->array[child_index + 1]) {
                // 则 child_index 标识右孩子
                child_index = child_index + 1;
            }
        }
        // 如果双亲的值大于 child 的值
        if (value > heap->array[child_index]) {
            heap->array[parent_index] = heap->array[child_index]; // 小节点上浮
            parent_index = child_index; // 更新双亲下标
            child_index = parent_index * 2 + 1; // 更新孩子下标
        } else { // 不做操作，跳出循环
            break;
        }
        // 大节点下沉
        heap->array[parent_index] = value;
    }
}

构造代码如下：

/**
 * @description: 构造最小堆
 * @param {BinaryHeap} *heap 二叉堆（无序）
 * @return {*} 无
 */
void create_min_heap(BinaryHeap *heap)
{
    // 每个非叶子结点都调整
    for (int i = (heap->length - 2) / 2; i >= 0; i--) {
        adjust_for_min_heap(heap, i);
    }
}

7.8.3.1. 插入结点

只需将新结点插入二叉堆最后一个结点的下一个位置，然后重新构造二叉堆。

以最小堆为例，代码如下：

/**
 * @description: 向最小堆中插入一个元素
 * @param {BinaryHeap} *heap 最小堆指针
 * @param {int} elem 新元素
 * @return {*} 无
 */
void insert_into_min_heap(BinaryHeap *heap, int elem)
{
    if (heap->length == MAXSIZE) {
        printf("二叉堆已满，无法插入。\n");
        return;
    }
    heap->array[heap->length] = elem; // 插入
    heap->length++; // 更新长度
    create_min_heap(heap); // 重新构造
}

7.8.3.2. 删除结点

将最后一个结点移动（赋值）到堆顶，然后重新构造二叉堆。

以最小堆为例，代码如下：

/**
 * @description: 删除最小堆的堆顶
 * @param {BinaryHeap} *heap 最小堆指针
 * @param {int} *elem 保存变量指针
 * @return {*} 无
 */
void delete_from_min_heap(BinaryHeap *heap, int *elem)
{
    if (heap->length == 0) {
        printf("二叉堆空，无元素可删。\n");
        return;
    }
    *elem = heap->array[0];
    heap->array[0] = heap->array[heap->length - 1]; // 移动到堆顶
    heap->length--; // 更新长度
    create_min_heap(heap); //重新构造
}

7.9. 优先队列

首先回忆一下队列的内容，只要记住八个字即可：先进先出（FIFO），后进后出（LILO）。

就像去医院门诊看病排队时一样：先来的先看，看完先走。

而优先队列的特性正是“优先”二字，“优先”二字意味着打破了“常规”“规则”。

优先队列不再遵守普通队列的先进先出的原则了，如何不遵守呢？

• 最大优先队列：不管入队顺序如何，谁的值最大谁先出队
• 最小优先队列：不管入队顺序如何，谁的值最小谁先出队

比如，对于最大优先队列，入队顺序为：14352，出队顺序则为：54321；对于最小优先队列，入队顺序为：14352，出队顺序则为：12345.

举个例子：医院的急诊病例，即便来的晚，也是可以优先看病的，因为生命至上。遇到灾难危险时，群众中会先疏散小孩子。

如果在诸如此类需要讲“优先”的情况下，再去讲什么“先进先出”的排队规则，那就不太好了。

那么该如何实现优先队列呢？

首先，在优先队列中，想要出队元素，肯定要先找到最大值，或者最小值；

其次，优先队列“不讲常规”，所以进队顺序已经不重要了，重要的是找到当前队列中的最大值或最小值。

那么，有没有一个能直接找到最大值或最小值，并不在意其它顺序的方法呢？

有！这个方法就是二叉堆！

1. 二叉堆的堆顶是该堆中的最大值或最小值
2. 插入一个结点，即插入到二叉堆的最末尾，然后会再次调整构成二叉堆
3. 删除一个结点，即删除堆顶，然后会再次调整构成二叉堆

所以可以借助二叉堆来实现优先队列，最大堆实现最大优先队列，最小堆实现最小优先队列

1. 出队即把堆顶出队
2. 入队即向二叉堆中插入一个结点
3. 出队即删除堆顶

天作之合！完美~

下面是最大优先队列的代码实现。

优先队列的结构体即是二叉堆的结构体：

typedef struct {
    int array[MAXSIZE];
    int length;
} BinaryHeap, PriorityQueue;

入队操作：

/**
 * @description: 最大优先队列入队
 * @param {PriorityQueue} *queue 队列指针
 * @param {int} elem 入队元素
 * @return {*} 无
 */
void en_max_queue(PriorityQueue *queue, int elem)
{
    insert_into_max_heap(queue, elem);
}

出队操作：

/**
 * @description: 最大优先队列出队
 * @param {PriorityQueue} *queue 队列指针
 * @param {int} *elem 保存变量指针
 * @return {*} 无
 */
void de_max_queue(PriorityQueue *queue, int *elem)
{
    delete_from_max_heap(queue, elem);
}

函数 insert_into_max_heap、delete_from_max_heap 的实现在上一节中已经实现了。