2013年蓝桥杯国赛C组危险系数（洛谷P8604）：图论算法解密

一、问题描述

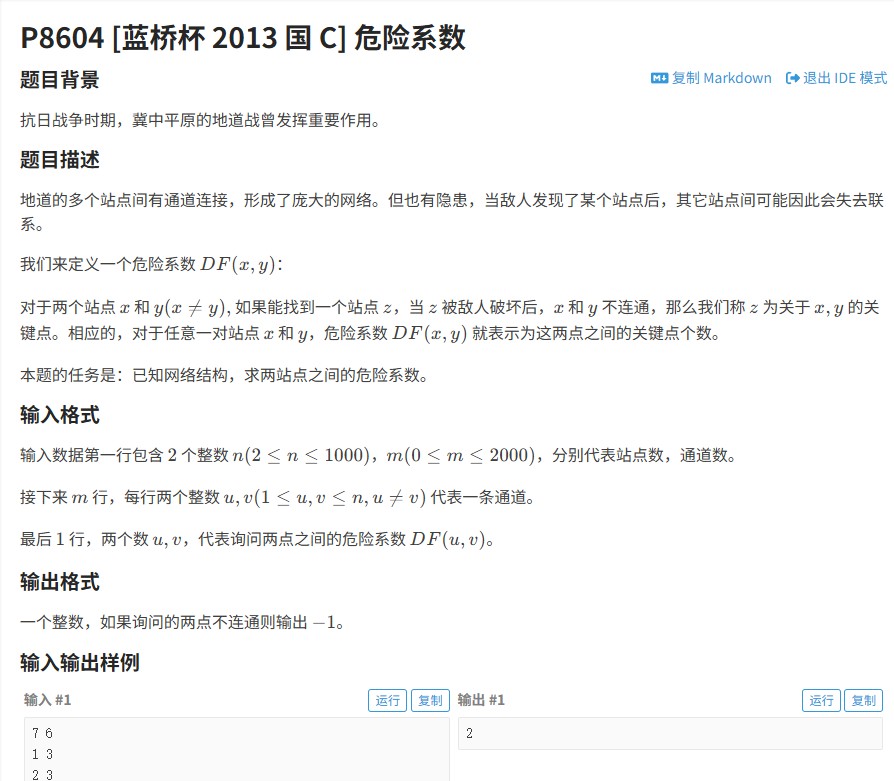
地下网络由多个站点和连接通道组成。当某个站点被敌人破坏后，可能导致其他站点间失去联系。危险系数DF(x,y)定义为：使站点x和y断开连接的所有关键点z的数量。

二、算法核心思想

图表示：使用邻接表存储网络结构
连通性检查：BFS 广度优先搜索算法
关键点判定：逐个排除节点后检查连通性

三、实现步骤

输入处理：读取站点数n、通道数m及所有通道
初始连通性检查：确保x和y初始连通
关键点检测：
- 遍历所有非x/y的站点z
- 暂时移除z后检查x和y的连通性
- 统计导致不连通的z的数量
结果输出：返回危险系数或-1（若不连通）

四、实现代码

#include <iostream>
#include <vector>
#include <queue>
using namespACe std;

const int MAXN = 1005;
vector<int> graph[MAXN]; // 邻接表存储图
bool visited[MAXN];

// BFS检查从u到v是否连通，忽略节点ignore
bool isConnected(int u, int v, int ignore, int n) {
    fill(visited, visited + n + 1, false);
    queue<int> q;
    q.push(u);
    visited[u] = true;
    visited[ignore] = true; // 标记忽略的节点为已访问

    while (!q.empty()) {
        int current = q.front();
        q.pop();

        for (int neighbor : graph[current]) {
            if (!visited[neighbor]) {
                if (neighbor == v) return true;
                visited[neighbor] = true;
                q.push(neighbor);
            }
        }
    }
    return false;
}

int main() {
    int n, m;
    cin >> n >> m;

    // 构建图
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        graph[u].push_back(v);
        graph[v].push_back(u);
    }

    int x, y;
    cin >> x >> y;

    // 首先检查初始连通性
    if (!isConnected(x, y, -1, n)) {
        cout << -1 << endl;
        return 0;
    }

    int count = 0;
    // 检查每个可能的z
    for (int z = 1; z <= n; z++) {
        if (z == x || z == y) continue; // 跳过x和y本身
        if (!isConnected(x, y, z, n)) {
            count++;
        }
    }

    cout << count << endl;
    return 0;
}