(1)代码题(leetcode类型),主要考察数据结构和基础算法,以及代码基本功
虽然这部分跟机器学习,深度学习关系不大,但也是面试的重中之重。基本每家公司的面试都问了大量的算法题和代码题,即使是商汤、face++这样的深度学习公司,考察这部分的时间也占到了我很多轮面试的60%甚至70%以上。我去face++面试的时候,面试官是residual net,shuffle net的作者;但他们的面试中,写代码题依旧是主要的部分。
大部分题目都不难,基本是leetcode medium的难度。但是要求在现场白板编程,思路要流畅,能做到一次性Bug-free. 并且,一般都是要给出时间复杂度和空间复杂度最优的做法。对于少数难度很大的题,也不要慌张。一般也不会一点思路也没有,尽力给面试官展现自己的思考过程。面试官也会引导你,给一点小提示,沿着提示把题目慢慢做出来也是可以通过面试的。
以下是我所遇到的一些需要当场写出完整代码的题目:
<1> 二分查找。分别实现C++中的lower_bound和upper_bound.
<2> 排序。 手写快速排序,归并排序,堆排序都被问到过。
时间复杂度可以到O(n)
<4> 给你一个数组,在这个数组中找出不重合的两段,让这两段的字段和的差的绝对值最大。
时间复杂度可以到O(n)
<5> 给你一个数组,求一个k值,使得前k个数的方差 + 后面n-k个数的方差最小
<6> 给你一个只由0和1组成的字符串,找一个最长的子串,要求这个子串里面0和1的数目相等。
时间复杂度可以到O(n)
<7> 给你一个数组以及一个数K, 从这个数组里面选择三个数,使得三个数的和小于等于K, 问有多少种选择的方法?
时间复杂度可以到O(n^2)
<8> 给你一个只由0和1组成的矩阵,找出一个最大的子矩阵,要求这个子矩阵是方阵,并且这个子矩阵的所有元素为1
时间复杂度可以到O(n^2)
<9> 求一个字符串的最长回文子串
时间复杂度可以到O(n) (Manacher算法)
<10> 在一个数轴上移动,初始在0点,现在要到给定的某一个x点, 每一步有三种选择,坐标加1,坐标减1,坐标乘以2,请问最少需要多少步从0点到x点。
<11> 给你一个集合,输出这个集合的所有子集。
<12> 给你一个长度为n的数组,以及一个k值(k < n) 求出这个数组中每k个相邻元素里面的最大值。其实也就是一个一维的max pooling
时间复杂度可以到O(n)
<13> 写一个程序,在单位球面上随机取点,也就是说保证随机取到的点是均匀的。
<14> 给你一个长度为n的字符串s,以及m个短串(每个短串的长度小于10), 每个字符串都是基因序列,也就是说只含有A,T,C,G这四个字母。在字符串中找出所有可以和任何一个短串模糊匹配的子串。模糊匹配的定义,两个字符串长度相等,并且至多有两个字符不一样,那么我们就可以说这两个字符串是模糊匹配的。
1、A为N*k矩阵,B为M*k的矩阵,求AB的欧式距离,要求用矩阵化的方法(不用for循环...)。
其中就是求一个distance矩阵。对A、B中的每一个元素直接求解他们的欧式距离。
一、for循环
分别对A和B中的数据进行循环遍历,计算每两个点之间的欧式距离,然后赋值给dist矩阵。

import numpy as np
def compute_squared_EDM_method(A,B):
# determin dimensions of data matrix
num1 = A.shape[0]
num2 = B.shape[0]
# initialize squared EDM D
dists = np.zeros((num1, num2))
# iterate over upper triangle of D
for i in range(num1):
for j in range(num2):
dists[i][j] = np.sqrt(np.sum(np.square(A[i] - B[j])))
return dists

二、使用矩阵运算的方法替代之前的循环操作。
dist=sqrt(A^2+B^2-2A.Bt)
dists = np.sqrt(-2 * np.dot(A, B.T) + np.sum(np.square(B), axis=1) + np.transpose(
[np.sum(np.square(A), axis=1)]))
2、给了个label和pred示例,计算AP写代码。
PR曲线:即 以 precision 和 recall 作为 纵、横轴坐标 的二维曲线。
AP值:Average Precision,即 平均精确度 。
如何衡量一个模型的性能,单纯用 precision 和 recall 都不科学。于是人们想到,哎嘛为何不把 PR曲线下的面积 当做衡量尺度呢?于是就有了 AP值 这一概念。这里的 average,等于是对 precision进行 取平均
mAP值:Mean Average Precision,即 平均AP值 。
是对多个验证集个体 求 平均AP值 。
Recall = TPR = TP/(TP+FN)
Precision = TP/(TP+FP) (精确度/率)
Accuracy = (TP+TN)/(P+N) = (TP+TN) / (TP + FN + FP + TN)(准确率,姑且这么叫吧,其中P为所有的正样本,N为所有的负样本)F-Meature = 2(Precision*Recall)/(Precision + Recall)
https://blog.csdn.net/Jesse_Mx/article/details/79169991SSD算法评估:AP, mAP和Precision-Recall曲线

for i in range(len(precisions) - 2, -1, -1):
precisions[i] = np.maximum(precisions[i], precisions[i + 1])
# Compute mean AP over recall range
indices = np.where(recalls[:-1] != recalls[1:])[0] + 1
mAP = np.sum((recalls[indices] - recalls[indices - 1]) *
precisions[indices])


[so,si]=sort(-out);%out is the result from your classifier
tp=gt(si)>0;
fp=gt(si)<0;
fp=cumsum(fp);%判为负样本的数
tp=cumsum(tp);%判为正样本的数
rec=tp/sum(gt>0);%召回率
prec=tp./(fp+tp);%精确度
ap=VOCap(rec,prec);
function ap = VOCap(rec,prec)
//matlab 计算AP的过程
mrec=[0 ; rec ; 1];
mpre=[0 ; prec ; 0];
for i=numel(mpre)-1:-1:1
mpre(i)=max(mpre(i),mpre(i+1));
end
i=find(mrec(2:end)~=mrec(1:end-1))+1;%去掉mrec中重复的部分,+1是保持下标的一致
ap=sum((mrec(i)-mrec(i-1)).*mpre(i));%area=(x(2)-x(1))*y

机器学习:Python实现聚类算法(二)之AP算法
3、一维maxpooling操作长度1*k,stride=1,窗口大小n,时间复杂度要求很小。

tf.layers.max_pooling1d(
inputs,
pool_size,
strides,
padding='valid',
data_format='channels_last',
name=None
)

- inputs:池的张量,秩必须为3。
- pool_size:单个整数的整数或元组/列表,表示池化窗口的大小。
- strides:单个整数的整数或元组/列表,指定池操作的步幅。
- padding:一个字符串,表示填充方法,可以是“valid”或“same”,不区分大小写。
- data_format:一个字符串,一个channels_last(默认)或channels_first,表示输入中维度的顺序,channels_last对应于具有形状(batch, length, channels)的输入,而channels_first对应于具有形状(batch, channels, length)的输入。
- name:字符串,图层的名称。
返回:
输出张量,秩为3。
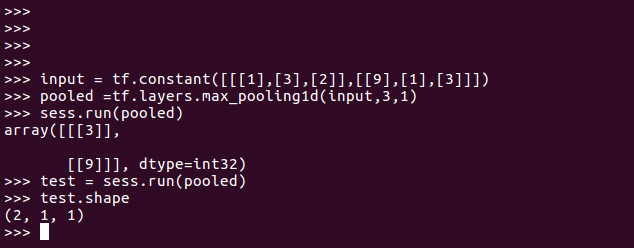
类似题目:对一个一维数组做核为k的max_pooling, 步长为1,并写出时间复杂度
max pooling 的操作如下图所示:整个图片被不重叠的分割成若干个同样大小的小块(pooling size)。每个小块内只取最大的数字,再舍弃其他节点后,保持原有的平面结构得出 output。
一维数组做max_pooling就是分段比较。

# max pooling
for r_idx in range(0,out_row):
for c_idx in range(0,out_col):
startX = c_idx * poolStride
startY = r_idx * poolStride
poolField = temp_map[startY:startY + poolSize, startX:startX + poolSize]
poolOut = np.max(poolField)
outputMap[r_idx,c_idx] = poolOut
# retrun outputMap
return outputMap

4、字符串反转 hello world ---> dlrow olleh。
String str = "Hello World"; //首先定义一个Hello World字符串
StringBuilder sb = new StringBuilder(str); //创建一个StringBuilder变量,将定义的字符串传递进去
System.out.println(sb.reverse().toString()); //使用StringBuilder里面的函数,将字符串反转,然后已字符串的方式输出。
hello world 输出 olleh dlrow
字符串翻转集合, case1, hello world->world hello; case2, hello world->olleh dlrow
Python实现字符串反转的几种方法
5、fast_Rcnn原理和实现
R-CNN,Fast R-CNN,Faster R-CNN原理及执行与训练的实例+实现自己的目标检测
用自己的数据训练Faster-RCNN,tensorflow版本(一)
6、
问:Pooling知道吧?我们在做cv的时候,图像经常是不同size的,我们在训练的时候经常通过crop图片取得同size的输入数据。但是训练的时候,输入是整张图,【这样会造成什么后果呢?】用没有什么办法可以解决这个问题呢?即测试的时候如何有效利用整张图的信息?
答:测试的时候也crop,每个croped图片有一个预测结果,通过投票的形式得到最后结果。
问:因为crop是overlapping的,这种方式会造成在部分图片区域上的重复卷积,增加计算复杂度,有没有办法解决这个问题?
答:在卷积输出层,也就是fc层前进行crop(但是网络结构不能改变)
问:怎么做呢?举个例子,原来是8x8x128的卷积输出层,换成全图之后,是10x12x128的卷积层,怎么连接到fc1层(假设是20维的)?
答:用20x8x8x128(n,c,h,w)的卷积核对10x12x128的map进行(s=1,p=0)的卷积,其实就相当于crop,得到fc1为20x3x5(c,h,w)的输出
问:但是此时fc1层改变了(从20编程20x3x5), fc2层与之的连接也就失效了, 怎么解决?
答:(用5x20x1x1的卷积核再操作,得到5x3x5的输出结果
要得到一个五维的输出向量,对3x5区域做一个平均就可以了(每个channel是3x5=15个结果,即对卷积层输出卷积操作得到3x5个不同feature预测的结果,就是15个crop对应的结果)
问:为什么选InceptionV3?
答:实现方便,top1正确率和其他比较新的模型差不多
[LeetCode] Maximum Product Subarray的4种解法
leetcode每日解题思路 221 Maximal Square
LeetCode:Subsets I II
(2)数学题或者"智力"题。
如果一个女生说,她集齐了十二个星座的前男友,我们应该如何估计她前男友的数量?
- 「秩」是图像经过矩阵变换之后的空间维度
- 「秩」是列空间的维度
矩阵低秩的意义?:低秩表征着一种冗余程度。
秩越低表示数据冗余性越大,因为用很少几个基就可以表达所有数据了。相反,秩越大表示数据冗余性越小。
一个m*n的矩阵,如果秩很低(秩r远小于m,n),则它可以拆成一个m*r矩阵和一个r*n矩阵之积(类似于SVD分解)。后面这两个矩阵所占用的存储空间比原来的m*n矩阵小得多。
VD的效果就是..用一个规模更小的矩阵去近似原矩阵...
这里A就是代表图像的原矩阵..其中的 尤其值得关注,它是由A的特征值从大到小放到对角线上的..也就是说,我们可以选择其中的某些具有“代表性”的特征值去近似原矩阵!
尤其值得关注,它是由A的特征值从大到小放到对角线上的..也就是说,我们可以选择其中的某些具有“代表性”的特征值去近似原矩阵!
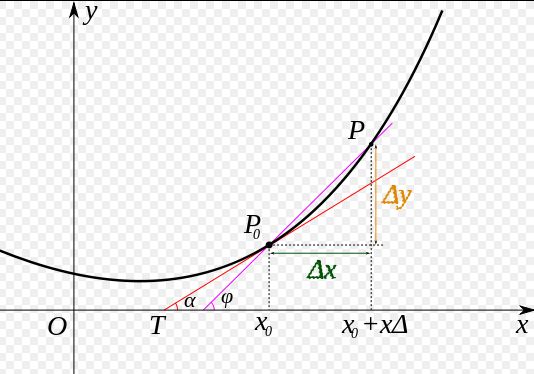
导数的几何意义可能很多人都比较熟悉: 当函数定义域和取值都在实数域中的时候,导数可以表示函数曲线上的切线斜率。 除了切线的斜率,导数还表示函数在该点的变化率。
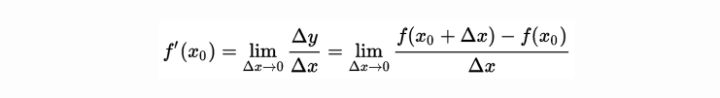
将上面的公式转化为下面图像为:
(3)机器学习基础
这两种算法都是基于回归的概念。
逻辑回归相对容易理解,就是通过Sigmoid函数将线性方程ax+b对应到一个隐状态P,P=S(ax+b),然后根据发生概率(p)与没有发生概率(1-p)的大小决定因变量的取值,0或者1。具体操作就是p除以1-p再取对数,这个变换增加了取值区间的范围;改变了函数值与自变量间的曲线关系,根据大量实验数据,这个变换往往能使函数值和自变量之间呈线性关系。
SVM则是通过一个非线性映射p,把样本空间映射到一个高维乃至无穷维的特征空间中(Hilbert空间),使得在原来的样本空间中非线性可分的问题转化为在特征空间中的线性可分的问题.简单地说,就是升维和线性化。作为分类、回归等问题来说,很可能在低维样本空间无法线性处理的样本集,在高维特征空间中却可以通过一个线性超平面实现线性划分(或回归)。一般的升维都会带来计算的复杂化,但SVM方法巧妙地应用核函数的展开定理简化了计算,不需要知道非线性映射的显式表达式
。简单来说,SVM是在高维特征空间中建立线性学习机,几乎不增加计算的复杂性,并且在某种程度上避免了“维数灾难”,这一切要归功于核函数的展开和计算理论.
综上所述,逻辑回归和SVM都可以用于分类问题的解决,其主要区别就在于映射函数选择上的不同,逻辑回归常用于处理大数据,而SVM则正好相反。
SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。
而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重,两者的根本目的都是一样的。
svm考虑局部(支持向量),而logistic回归考虑全局,
1.损失函数不一样,逻辑回归的损失函数是log loss,svm的损失函数是hinge loss
2.损失函数的优化方法不一样,逻辑回归用剃度下降法优化,svm用smo方法进行优化
3.逻辑回归侧重于所有点,svm侧重于超平面边缘的点
4.svm的基本思想是在样本点中找到一个最好的超平面
相同点:
1,LR和SVM都是分类算法。
2,如果不考虑核函数,LR和SVM都是线性分类算法,即分类决策面都是线性的。
3,LR和SVM都是监督学习算法。
不同点:
1,本质上是其loss function不同。
2,支持向量机只考虑局部的边界线附近的点,而逻辑回归考虑全局(远离的点对边界线的确定也起作用)。
线性SVM不直接依赖于数据分布,分类平面不受一类点影响;LR则受所有数据点的影响,如果数据不同类别strongly unbalance,一般需要先对数据做balancing。
3,在解决非线性问题时,支持向量机采用核函数的机制,而LR通常不采用核函数的方法。
这个问题理解起来非常简单。分类模型的结果就是计算决策面,模型训练的过程就是决策面的计算过程。通过上面的第二点不同点可以了解,在计算决策面时,SVM算法里只有少数几个代表支持向量的样本参与了计算,也就是只有少数几个样本需要参与核计算(即kernal machine解的系数是稀疏的)。然而,LR算法里,每个样本点都必须参与决策面的计算过程,也就是说,假设我们在LR里也运用核函数的原理,那么每个样本点都必须参与核计算,这带来的计算复杂度是相当高的。所以,在具体应用时,LR很少运用核函数机制。
4,线性SVM依赖数据表达的距离测度,所以需要对数据先做normalization,LR不受其影响。
5,SVM的损失函数就自带正则!!!(损失函数中的1/2||w||^2项),这就是为什么SVM是结构风险最小化算法的原因!!!而LR必须另外在损失函数上添加正则项!!!
本节来自算法比较-SVM和logistic回归,该博客里有些写的并不准确,具有参考价值。
在Andrew NG的课里讲到过:
1. 如果Feature的数量很大,跟样本数量差不多,这时候选用LR或者是Linear Kernel的SVM
2. 如果Feature的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gaussian Kernel
3. 如果Feature的数量比较小,而样本数量很多,需要手工添加一些feature变成第一种情况
可以说神经网络是通过多个感知器(Perceptron)的组合叠加来解决非线性的分类问题. 而SVM通过核函数视图非线性的问题的数据集转变为核空间中一个线性可分的数据集.
另外, 神经网络非常依赖参数. 比如学习率, 隐含层的结构与节点个数. 参数的好坏会极大影响神经网络的分类效果. 而SVM是基于最大边缘的思想, 只有少量的参数需要调整.
各种机器学习的应用场景分别是什么?例如,k近邻,贝叶斯,决策树,svm,逻辑斯蒂回归和最大熵模型。
主成分分析,奇异值分解
PCA是一种无监督学习,其存在的假设是:_方差越大信息量越多_。但是信息(方差)小的特征并不代表表对于分类没有意义,可能正是某些方差小的特征直接决定了分类结果,而PCA在降维过程中完全不考虑目标变量的做法会导致一些关键但方差小的分类信息被过滤掉。
随机森林,GBDT, 集成学习
为什么说bagging是减少variance,而boosting是减少bias?
基于树的adaboost和Gradient Tree Boosting区别?
为什么在实际的 kaggle 比赛中 gbdt 和 random forest 效果非常好?
过拟合
1 获取更多数据,2 数据增强&噪声数据3 简化模型.
提前终止,L1和L2正则化
正则化的一个最强大最知名的特性就是能向损失函数增加“惩罚项”(penalty)。所谓『惩罚』是指对损失函数中的某些参数做一些限制。最常见的惩罚项是L1和L2:
- L1惩罚项的目的是将权重的绝对值最小化
- L2惩罚项的目的是将权重的平方值最小化
Dropout-深度学习
机器学习中使用「正则化来防止过拟合」到底是一个什么原理?为什么正则化项就可以防止过拟合?
(4)深度学习基础
卷积神经网络,循环神经网络,LSTM与GRU,梯度消失与梯度爆炸,激活函数,防止过拟合的方法,dropout,batch normalization,各类经典的网络结构,各类优化方法
卷积神经网络的复杂度分析:时间和空间,以及影响。
CNN(卷积神经网络)、RNN(循环神经网络)、DNN(深度神经网络)的内部网络结构有什么区别?
sgd有多种改进的形式(rmsprop,adadelta等),为什么大多数论文中仍然用sgd?
你有哪些deep learning(rnn、cnn)调参的经验?
深度学习中 Batch Normalization为什么效果好?













