吾日三省吾身:为人谋而不忠乎?与朋友交而不信乎?传不习乎?
导读: 我们介绍过用matplotlib制作图表的一些tips,感兴趣的同学可以戳→纯干货:手把手教你用Python做数据可视化(附代码)。matplotlib是一个相当底层的工具。你可以从其基本组件中组装一个图表:数据显示(即绘图的类型:线、条、框、散点图、轮廓等)、图例、标题、刻度标记和其他注释。
在pandas中,我们可能有多个数据列,并且带有行和列的标签。pandas自身有很多内建方法可以简化从DataFrame和Series对象生成可视化的过程。另一个是seaborn,它是由Michael Waskom创建的统计图形库。seaborn简化了很多常用可视化类型的生成。
导入seaborn会修改默认的matplotlib配色方案和绘图样式,这会提高图表的可读性和美观性。 即使你不适用seaborn的API,你可能更喜欢导入seaborn来为通用matplotlib图表提供更好的视觉美观度。
作者:Wes McKinney
本文摘编自《利用Python进行数据分析》(原书第2版),如需转载请联系我们
01 折线图
Series和DataFrame都有一个plot属性,用于绘制基本的图型。默认情况下,plot()绘制的是折线图(见图9-13):
In [60]: s = pd.Series(np.random.randn(10).cumsum(), index=np.arange(0, 100, 10))
In [61]: s.plot()
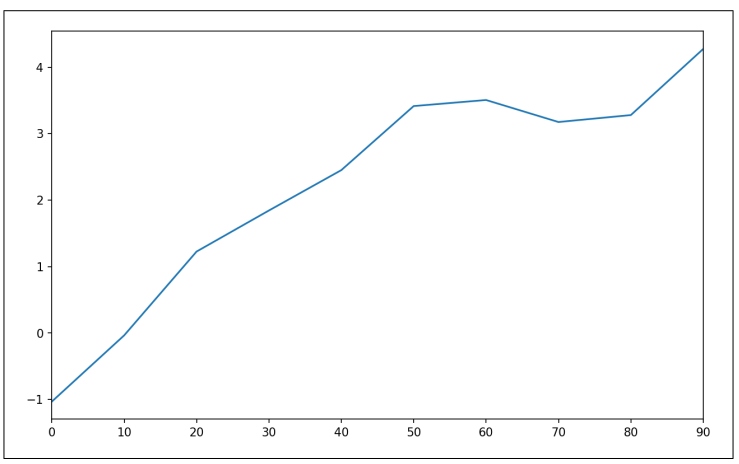
▲图9-13 简单序列图形
Series对象的索引传入matplotlib作为绘图的x轴,你可以通过传入use_index=False来禁用这个功能。x轴的刻度和范围可以通过xticks和xlim选项进行调整,相应地y轴使用yticks和ylim进行调整。表9-3是plot的全部选项列表。本节我会介绍这些选项中的一些,其余你可以自行探索。
大部分pandas的绘图方法,接收可选的ax参数,该参数可以是一个matplotlib子图对象。这使你可以更为灵活的在网格布局中放置子图。
DataFrame的plot方法在同一个子图中将每一列绘制为不同的折线,并自动生成图例(见图9-14):
In [62]: df = pd.DataFrame(np.random.randn(10, 4).cumsum(0),
....: columns=['A', 'B', 'C', 'D'],
....: index=np.arange(0, 100, 10))
In [63]: df.plot()
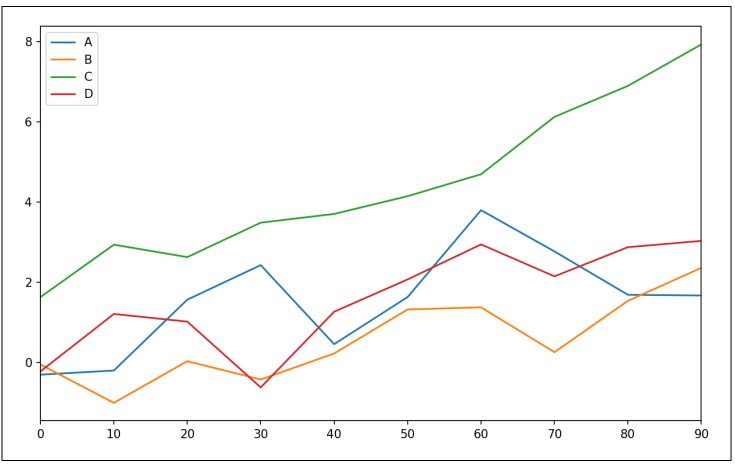
▲图9-14 简单DataFrame绘图
plot属性包含了不同绘图类型的方法族。例如,df.plot( )等价于df.plot.line( )。我们之后将会探索这些方法中的一部分。
要绘制的其他关键字参数会传递到相应的matplotlib绘图函数,因此你可以通过了解更多的matplotlib的 API信息来进一步定制这些图表。
参数 | 描述 |
label | 图例标签 |
ax | 绘图所用的matplotlib子图对象;如果没传值,则使用当前活动的matplotlib子图 |
style | 传给matplotlib的样式字符串,比如'ko--' |
alpha | 图片不透明度(从0到1) |
kind | 可以是 'area'、 'bar'、 'barh'、 'density'、'hist'、 'kde'、 'line'、 'pie' |
logy | 在y轴上使用对数缩放 |
use_index | 使用对象索引刻度标签 |
rot | 刻度标签的旋转(0到360) |
xticks | 用于x轴刻度的值 |
yticks | 用于y轴 |
xlim | x轴范围(例如[0,10]) |
ylim | y轴范围 |
grid | 展示轴网格(默认是打开的) |
▲表9-3 Series.plot方法参数
DataFrame拥有多个选项,允许灵活地处理列;例如,是否将各列绘制到同一个子图中,或为各列生成独立的子图。参考表9-4了解更多选项。
参数 | 描述 |
subplots | 将DataFrame的每一列绘制在独立的子图中 |
sharex | 如果subplots=True,则共享相同的x轴、刻度和范围 |
sharey | 如果subplots=True,则共享相同的y轴 |
figsize | 用于生成图片尺寸的元组 |
title | 标题字符串 |
legend | 添加子图图例(默认是True) |
sort_columns | 按字母顺序绘制各列,默认情况下使用已有的列顺序 |
▲表9-4
02 柱状图
plot.bar()和plot.barh()可以分别绘制垂直和水平的柱状图。在绘制柱状图时,Series或DataFrame的索引将会被用作x轴刻度(bar)或y轴刻度(barh)(参考图9-15):
In [64]: fig, axes = plt.subplots(2, 1)
In [65]: data = pd.Series(np.random.rand(16), index=list('abcdefghijklmnop'))
In [66]: data.plot.bar(ax=axes[0], color='k', alpha=0.7)
Out[66]: <matplotlib.axes._subplots.AxesSubplot at 0x7fb62493d470>
In [67]: data.plot.barh(ax=axes[1], color='k', alpha=0.7)
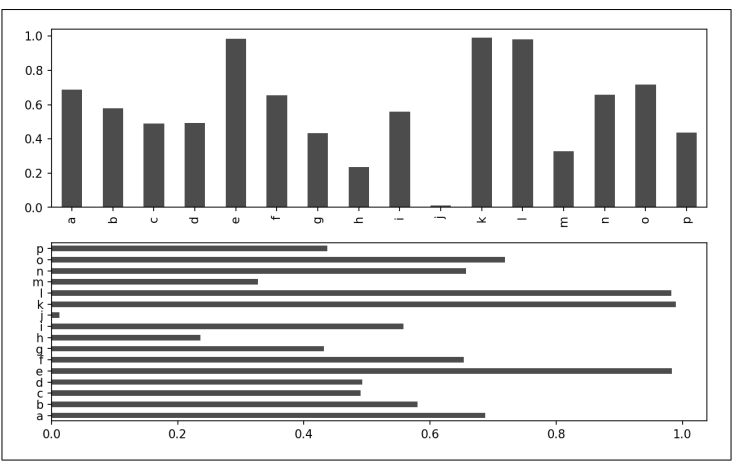
▲图9-15 水平柱状图和垂直柱状图
选项color='k'和alpha=0.7将柱子的颜色设置为黑色,并将图像的填充色设置为部分透明。
在DataFrame中,柱状图将每一行中的值分组到并排的柱子中的一组。参考图9-16:
In [69]: df = pd.DataFrame(np.random.rand(6, 4),
....: index=['one', 'two', 'three', 'four', 'five', 'six'],
....: columns=pd.Index(['A', 'B', 'C', 'D'], name='Genus'))
In [70]: df
Out[70]:
Genus A B C D
one 0.370670 0.602792 0.229159 0.486744
two 0.420082 0.571653 0.049024 0.880592
three 0.814568 0.277160 0.880316 0.431326
four 0.374020 0.899420 0.460304 0.100843
five 0.433270 0.125107 0.494675 0.961825
six 0.601648 0.478576 0.205690 0.560547
In [71]: df.plot.bar()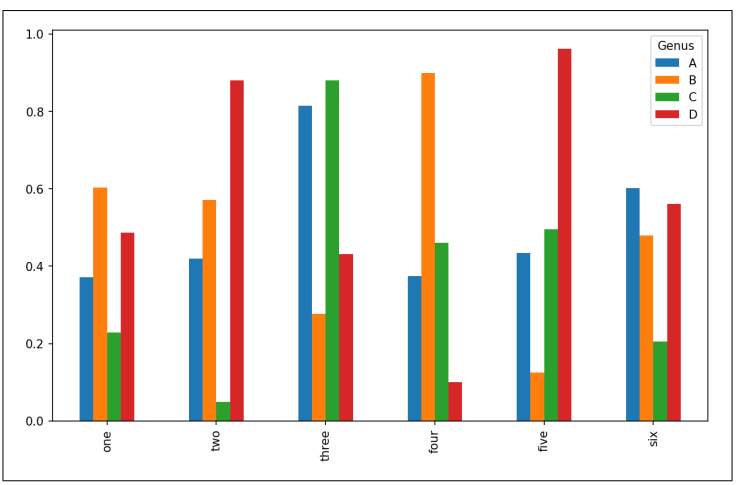
▲图9-16 DataFrame柱状图
请注意DataFrame的列名称"Genus"被用作了图例标题。我们可以通过传递stacked=True来生成堆积柱状图,会使得每一行的值堆积在一起(参考图9-17):
In [73]: df.plot.barh(stacked=True, alpha=0.5)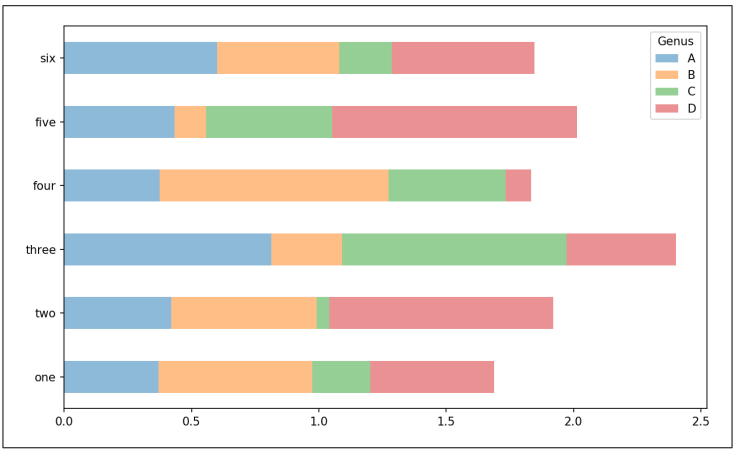
▲图9-17 DataFrame堆积柱状图
使用value_counts: s.value_counts().plot.bar()可以有效的对Series值频率进行可视化。
回到本书之前使用的数据集,假设我们想要绘制一个堆积柱状图,用于展示每个派对在每天的数据点占比。使用read_csv载入数据,并根据星期几数值和派对规模进形成交叉表:
In [75]: tips = pd.read_csv('examples/tips.csv')
In [76]: party_counts = pd.crosstab(tips['day'], tips['size'])
In [77]: party_counts
Out[77]:
size 1 2 3 4 5 6
day
Fri 1 16 1 1 0 0
Sat 2 53 18 13 1 0
Sun 0 39 15 18 3 1
Thur 1 48 4 5 1 3
# 没有太多的1人和6人派对
In [78]: party_counts = party_counts.loc[:, 2:5]之后,进行标准化以确保每一行的值和为1,然后进行绘图(见图9-18):
# 标准化至和为1
In [79]: party_pcts = party_counts.div(party_counts.sum(1), axis=0)
In [80]: party_pcts
Out[80]:
size 2 3 4 5
day
Fri 0.888889 0.055556 0.055556 0.000000
Sat 0.623529 0.211765 0.152941 0.011765
Sun 0.520000 0.200000 0.240000 0.040000
Thur 0.827586 0.068966 0.086207 0.017241
In [81]: party_pcts.plot.bar()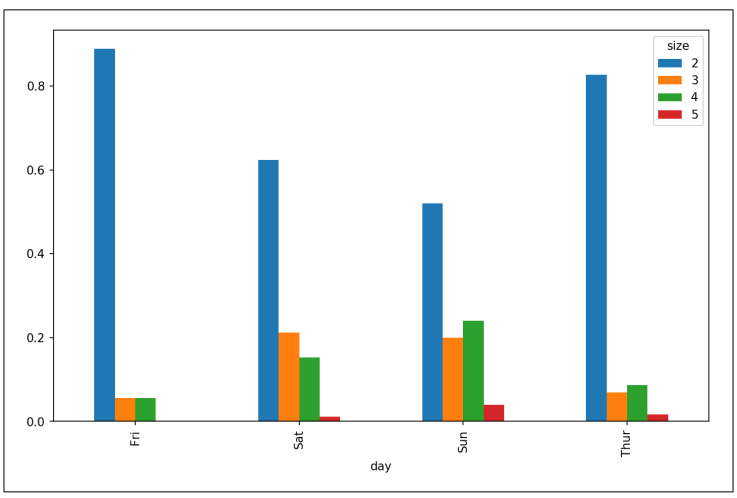
▲图9-18 每天派对数量的百分比
你可以看到本数据集中的派对数量在周末会增加。
对于在绘图前需要聚合或汇总的数据,使用seaborn包会使工作更为简单。现在让我们看下使用seaborn进行按星期几数值计算小费百分比(见图9-19中的结果图):
In [83]: import seaborn as sns
In [84]: tips['tip_pct'] = tips['tip'] / (tips['total_bill'] - tips['tip'])
In [85]: tips.head()
Out[85]:
total_bill tip smoker day time size tip_pct
0 16.99 1.01 No Sun Dinner 2 0.063204
1 10.34 1.66 No Sun Dinner 3 0.191244
2 21.01 3.50 No Sun Dinner 3 0.199886
3 23.68 3.31 No Sun Dinner 2 0.162494
4 24.59 3.61 No Sun Dinner 4 0.172069
In [86]: sns.barplot(x='tip_pct', y='day', data=tips, orient='h')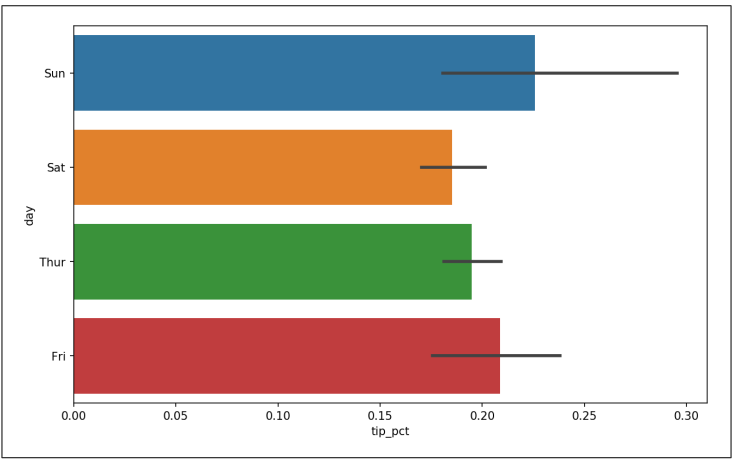
▲图9-19 用错误栏按天显示小费百分比
seaborn中的绘图函数使用一个data参数,这个参数可以是pandas的DataFrame。其他的参数则与列名有关。因为day列中有多个观测值,柱子的值是tip_pct的平均值。柱子上画出的黑线代表的是95%的置信区间(置信区间可以通过可选参数进行设置)。
seaborn.barplot拥有一个hue选项,允许我们通过一个额外的分类值将数据分离:
In [88]: sns.barplot(x='tip_pct', y='day', hue='time', data=tips, orient='h')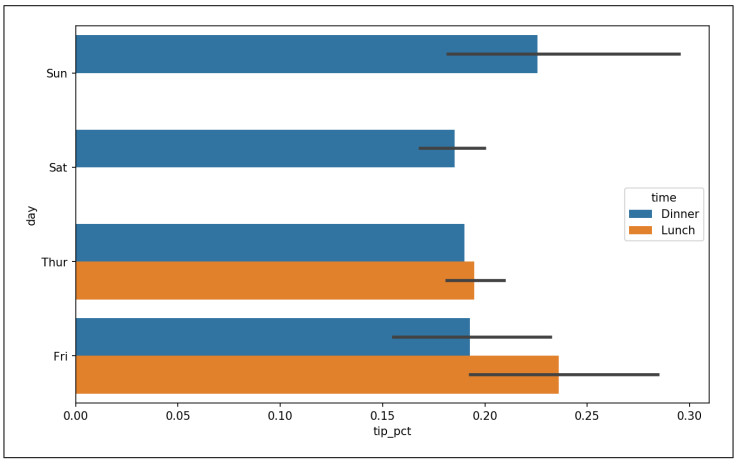
▲图9-20 根据星期几数值和时间计算的小费百分比
请注意seaborn自动改变了图表的美观性:默认的调色板、图背景和网格线条颜色。你可以使用seaborn.set在不同的绘图外观中进行切换:
In [90]: sns.set(style="whitegrid")03 直方图和密度图
直方图是一种条形图,用于给出值频率的离散显示。数据点被分成离散的,均匀间隔的箱,并且绘制每个箱中数据点的数量。使用之前的小费数据,我们可以使用Series的plot.hist方法制作小费占总费用百分比的直方图(见图9-21):
In [92]: tips['tip_pct'].plot.hist(bins=50)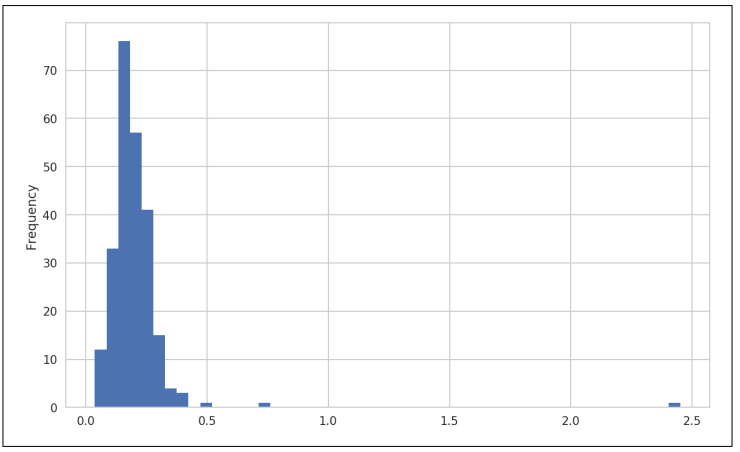
▲图9-21 小费百分比的直方图
密度图是一种与直方图相关的图表类型,它通过计算可能产生观测数据的连续概率分布估计而产生。通常的做法是将这种分布近似为“内核”的混合,也就是像正态分布那样简单的分布。因此,密度图也被成为内核密度估计图(KDE)。plot.kde使用传统法定混合法估计绘制密度图(见图9-22):
In [94]: tips['tip_pct'].plot.density()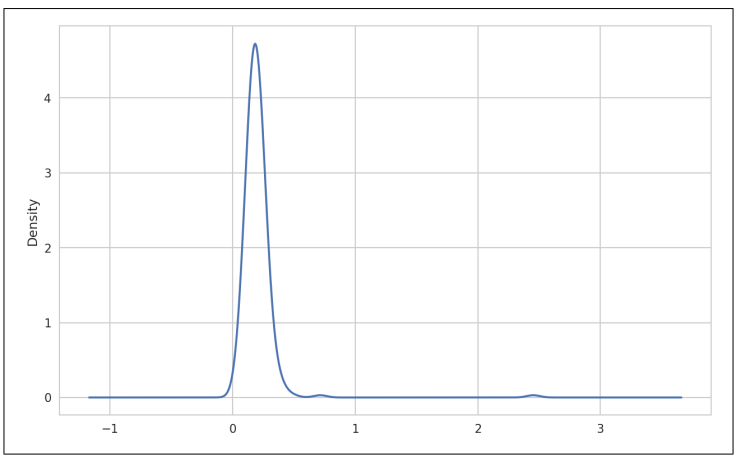
▲图9-22 小费百分比密度图
distplot方法可以绘制直方图和连续密度估计,通过distplot方法seaborn使直方图和密度图的绘制更为简单。作为例子,考虑由两个不同的标准正态分布组成的双峰分布(见图9-23):
In [96]: comp1 = np.random.normal(0, 1, size=200)
In [97]: comp2 = np.random.normal(10, 2, size=200)
In [98]: values = pd.Series(np.concatenate([comp1, comp2]))
In [99]: sns.distplot(values, bins=100, color='k')
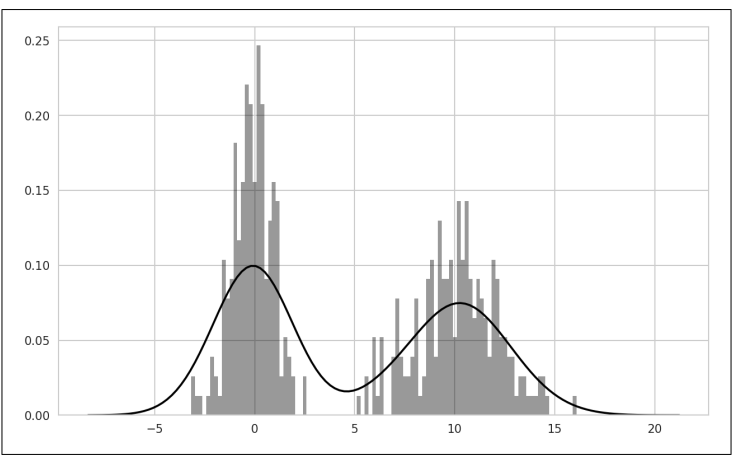
▲图9-23 正态混合的标准化直方图与密度估计
04 散点图或点图
点图或散点图可以用于检验两个一维数据序列之间的关系。例如,这里我们从statsmodels项目中载入了macrodata数据集,并选择了一些变量,之后计算对数差:
In [100]: macro = pd.read_csv('examples/macrodata.csv')
In [101]: data = macro[['cpi', 'm1', 'tbilrate', 'unemp']]
In [102]: trans_data = np.log(data).diff().dropna()
In [103]: trans_data[-5:]
Out[103]:
cpi m1 tbilrate unemp
198 -0.007904 0.045361 -0.396881 0.105361
199 -0.021979 0.066753 -2.277267 0.139762
200 0.002340 0.010286 0.606136 0.160343
201 0.008419 0.037461 -0.200671 0.127339
202 0.008894 0.012202 -0.405465 0.042560然后我们可以使用seaborn的reglot方法,该方法可以绘制散点图,并拟合出一个条线性回归线(见图9-24):
In [105]: sns.regplot('m1', 'unemp', data=trans_data)
Out[105]: <matplotlib.axes._subplots.AxesSubplot at 0x7fb613720be0>
In [106]: plt.title('Changes in log %s versus log %s' % ('m1', 'unemp'))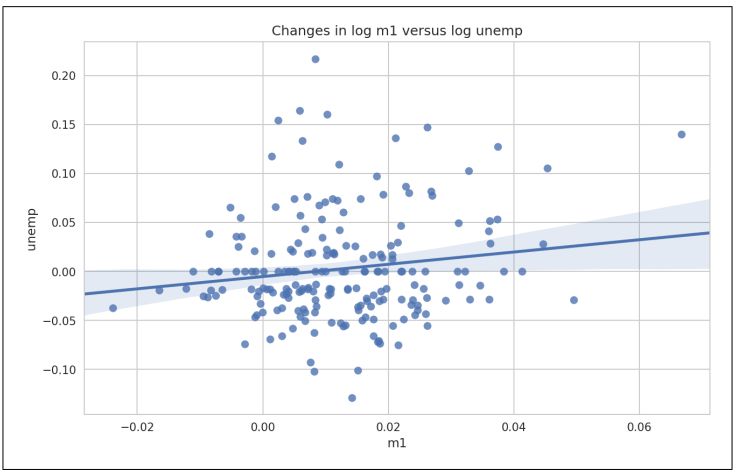
▲图9-24 seaborn回归/散点图
在探索性数据分析中,能够查看一组变量中的所有散点图是有帮助的; 这被称为成对图或散点图矩阵。从头开始绘制这样一个图是有点工作量的,所以seaborn有一个方便的成对图函数,它支持在对角线上放置每个变量的直方图或密度估计值(结果图见图9-25):
In [107]: sns.pairplot(trans_data, diag_kind='kde', plot_kws={'alpha': 0.2})
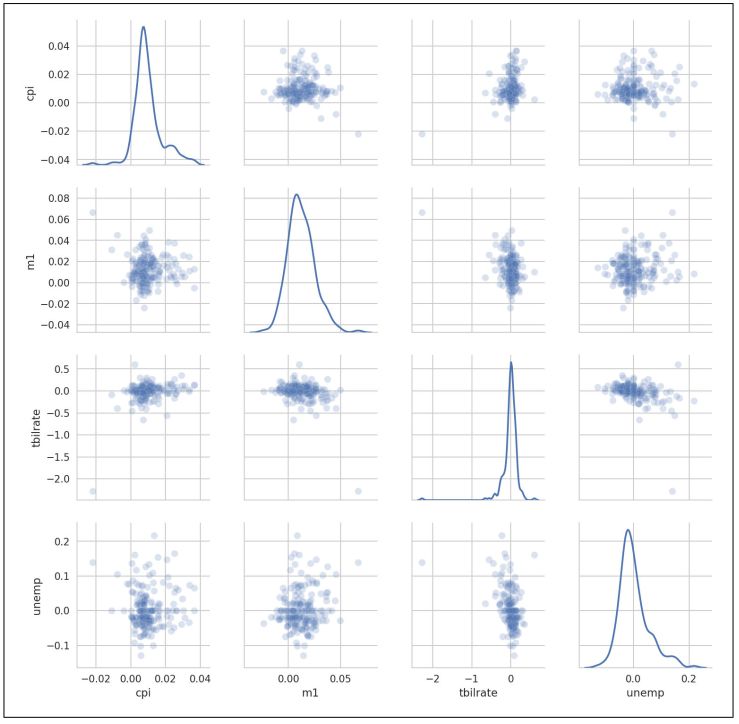
▲图9-25 statsmodels macro数据的成对图矩阵
你可能会注意到plot_ksw参数,这个参数使我们能够将配置选项传递给非对角元素上的各个绘图调用。参考seaborn.pairplot的文档字符串可以看到更多细节的设置选项。
05 分面网格和分类数据
如果数据集有额外的分组维度怎么办?使用分面网格是利用多种分组变量对数据进行可视化的方式。seaborn拥有一个有效的内建函数factorplot,可以简化多种分面绘图(见图9-26):
In [108]: sns.factorplot(x='day', y='tip_pct', hue='time', col='smoker',
.....: kind='bar', data=tips[tips.tip_pct < 1])

▲图9-26 按星期几数值/时间/是否吸烟划分的小费百分比
除了根据'time'在一个面内将不同的柱分组为不同的颜色,我们还可以通过每个时间值添加一行来扩展分面网格(见图9-27):
In [109]: sns.factorplot(x='day', y='tip_pct', row='time',
.....: col='smoker',
.....: kind='bar', data=tips[tips.tip_pct < 1])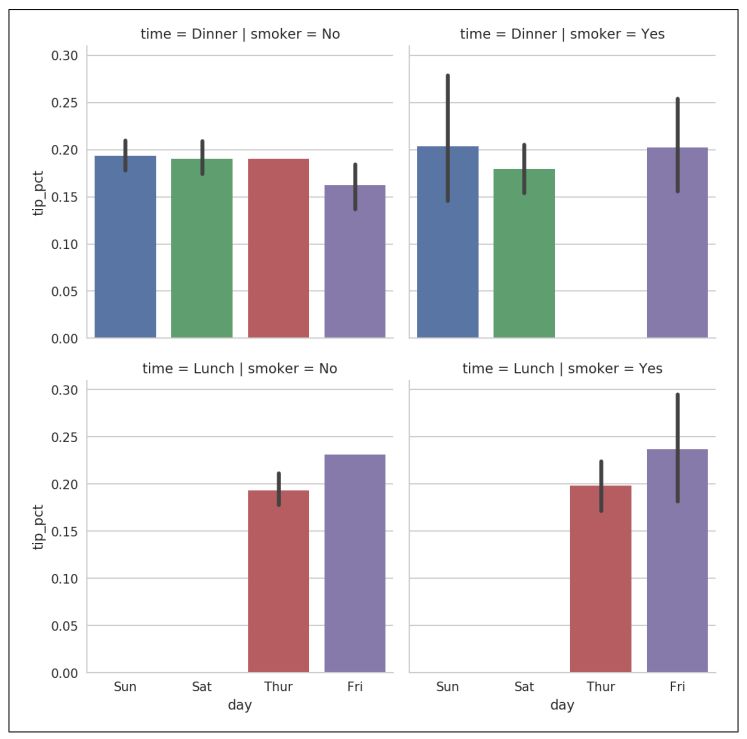
▲图9-27 根据时间/是否吸烟分面后按星期几数值划分的小费百分比
factorplot 支持其他可能有用的图类型,具体取决于你要显示的内容。 例如,箱形图(显示中位值,四分位数和异常值)可以是有效的可视化类型(图9-28):
In [110]: sns.factorplot(x='tip_pct', y='day', kind='box',
.....: data=tips[tips.tip_pct < 0.5])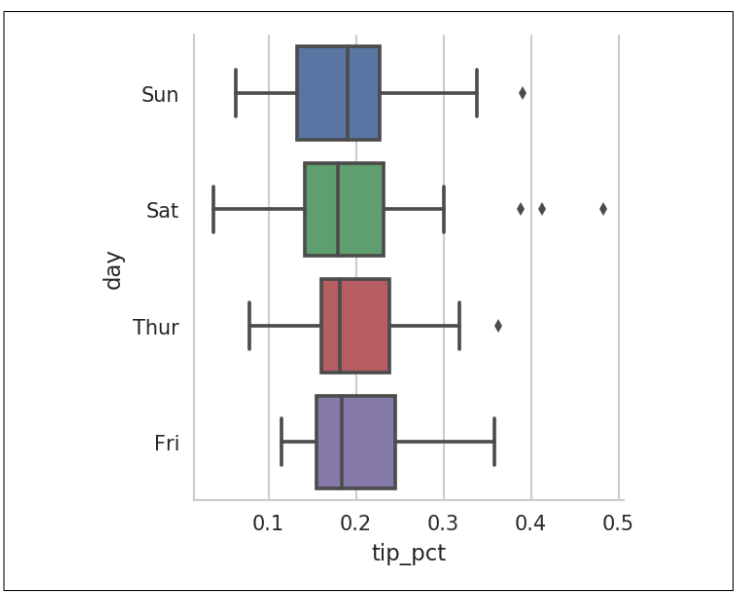
▲图9-28 根据星期几数值绘制的小费百分比箱型图
你可以使用更通用的seaborn.FacetGrid类创建自己的分面网格图。 具体请查看更多的seaborn文档。
06 其他Python可视化工具
和开源代码一样,在Python语言下创建图形的选择有很多(太多而无法一一列举)。自从2010年以来,很多开发工作都集中在创建web交互式图形上。借助像Bokeh和Plotly这样的工具,在web浏览器中创建动态的、交互式图像的工作现在已经可以实现。
如果是创建用于印刷或网页的静态图形,我建议根据你的需要使用默认的matplotlib以及像pandas和seaborn这样的附加库。 对于其他数据可视化要求,学习其他可用工具之一可能是有用的。我鼓励你探索Python可视化生态系统,因为它将持续增添新内容并在未来进行更多创新。
关于作者:韦斯·麦金尼(Wes McKinney)是流行的Python开源数据分析库pandas的创始人。他是一名活跃的演讲者,也是Python数据社区和Apache软件基金会的Python/C++开源开发者。目前他在纽约从事软件架构师工作。
本文摘编自《利用Python进行数据分析》(原书第2版),经出版方授权发布。
延伸阅读《利用Python进行数据分析》
点击上图了解及购买
推荐语:Python数据分析经典畅销书全新升级,第1版中文版累计销售100000册。针对Python 3.6进行全面修订和更新,涵盖新版的pandas、NumPy、IPython和Jupyter。

欢迎各位大佬点击链接加入群聊【helloworld开发者社区】:https://jq.qq.com/?_wv=1027&k=mBlk6nzX进群交流IT技术热点。
本文转自 https://mp.weixin.qq.com/s/a1ZvJ0mJbNizZcw3EbDHmA,如有侵权,请联系删除。















