 一、题目解读
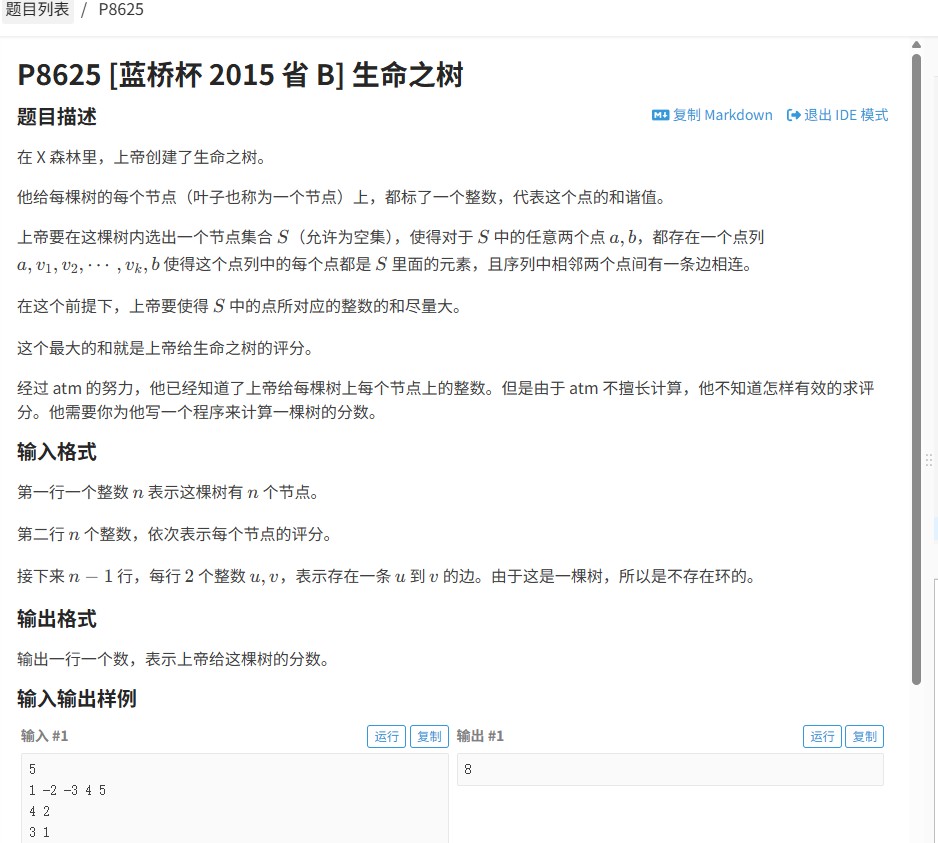
“生命之树”是一道经典的树形结构问题,要求计算一棵带权树中,以某个节点为根的最大子树权值和。题目输入为n个节点及边信息,每个节点有权值wi,需找到所有节点中,子树权值和最大的节点,并输出其值。核心挑战在于如何处理树形结构的递归关系,并高效聚合子节点信息。
一、题目解读
“生命之树”是一道经典的树形结构问题,要求计算一棵带权树中,以某个节点为根的最大子树权值和。题目输入为n个节点及边信息,每个节点有权值wi,需找到所有节点中,子树权值和最大的节点,并输出其值。核心挑战在于如何处理树形结构的递归关系,并高效聚合子节点信息。
二、解题思路 采用树形DP(Tree Dynamic Programming)策略,通过深度优先搜索(DFS)递归计算每个节点的贡献值。关键在于:
1. 状态定义:定义f[u]为以节点u为根的子树最大权值和。
2. 递归转移:遍历u的所有子节点v,若f[v]为正,则累加到f[u](排除负贡献子树)。
3. 结果更新:递归过程中维护全局最大值res,记录所有节点子树权和的最大值。
4.利用树形结构的递归性质,将复杂问题分解为子树求解,避免重复计算。三、解题步骤
1. 输入处理:读取n个节点权值w[],以及n-1条边信息构建邻接表g[]。
2. 初始化:设置res为极小值,确保首次更新有效。
3. 递归计算:从根节点1开始DFS,递归函数dfs(u, fa)计算u的子树权和,并排除父节点fa避免回溯。
4. 结果输出:最终res即为全局最优解。四、代码与注释
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 1e5 + 10; // 节点数上限
vector<int> g[MAXN]; // 邻接表存图
int w[MAXN]; // 节点权值
long long f[MAXN]; // 子树权和数组
long long res = -1e18; // 全局最大值(初始化为极小值)
// 递归计算以u为根的子树权和
void dfs(int u, int fa) {
f[u] = w[u]; // 初始化为节点自身权值
for (int v : g[u]) { // 遍历子节点
if (v == fa) continue; // 跳过父节点(避免反向遍历)
dfs(v, u); // 递归计算子树
if (f[v] > 0) f[u] += f[v]; // 累加正贡献子树
}
res = max(res, f[u]); // 更新全局最大值
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); // 加快输入输出
int n;
cin >> n;
for (int i = 1; i <= n; ++i) cin >> w[i]; // 读入权值
for (int i = 1; i < n; ++i) {
int u, v;
cin >> u >> v;
g[u].push_back(v); // 建边双向
g[v].push_back(u);
}
dfs(1, -1); // 从根节点1开始递归,-1表示无父节点
cout << res << endl;
return 0;
}五、总结 本解法通过树形DP将树形结构问题转化为子树递归求解,关键在于设计合理的状态转移方程,并利用动态规划避免重复计算。时间复杂度为O(n),空间复杂度O(n),适用于大规模树形数据。建议读者掌握树形DP的通用框架,结合题目特性优化状态设计。同时,递归时的剪枝(如排除负贡献子树)是提升效率的关键技巧。 原文:【蓝桥杯2015省赛解析】生命之树:树形DP解题全攻略(洛谷P8625代码详解)