题目
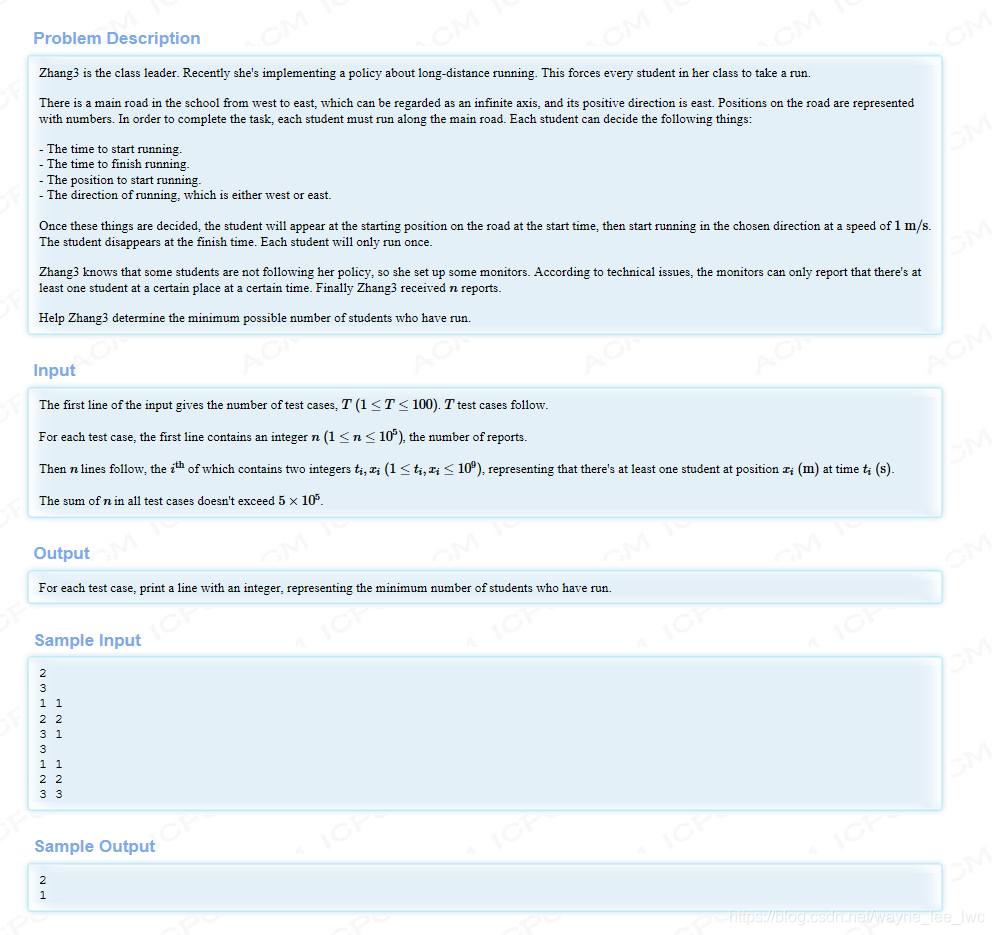
题目大意是这样的:在一条双向的轴上,有若干同学在跑步,每位同学的速度是固定的,都是1单位长度/s。在n个时刻t,位置
x上将至少有一个人在跑步,但是方向不确定,仅能确定有人。
需要求解的问题就是根据这n个时刻的信息,问能确定最少有多少同学在跑步?
二分图匹配
首先这个问题,以时间为横轴,位置为纵轴建系x-t图像,将n个数据描点。
题目中提到学生跑步有起始时间和终止时间,反映在坐标系上就是一条线段。但是由于题目要求的是最小的学生数量,因此不妨假设学生跑步时间是无限长,且开始的无限早,这反映在坐标系上就是一条直线。
也就是说倘若一个学生在向正方向跑,那么其跑出的直线斜率为1,反之斜率为-1。
如果两个点描述的是同一个学生,那么这两个点就在同一条直线上。
那么问题就转变成了给定n个点,使用斜率为1或者-1的直线覆盖这些点,问最少直线数量是多少?
斜率为-1或1不太好处理,我们不妨将坐标轴顺时针旋转45°。
我们假设原横纵坐标为t,p;
可使用矩阵乘法进行旋转:
[ x y ] = [ 1 1 1 − 1 ] [ t p ] \begin{bmatrix} x\\ y \end{bmatrix}= \begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} \begin{bmatrix} t\\ p \end{bmatrix} [xy]=[111−1][tp]
即:
{ x = t + p y = t − p \left\{\begin{matrix} x= t + p\\ y=t - p \end{matrix}\right. {x=t+py=t−p
写在程序中可以直接写成:
int x,y;
scanf("%d%d",&x,&y);
x += y;
y = x - y * 2;
这样旋转之后,所有 斜率为1的直线都是平行于x轴的直线,所有斜率为-1的直线都是品性与y轴的直线。
(其实仔细思考一下,如果学生向负方向跑步那么他所有出现点,时间和位置的加和不变,如果向正方向跑,其时间和位置的差不变)
下面我们可以建立一个二分图,左边是横坐标,右边是纵坐标。对于点(xi,yi),我们将xi和yi连一条边。
接着,如果我们选择一个左边的点xi即等于选择了一条直线 x=xi ,同理右边的点yi代表着直线 y=yi 。对于没跳变,都要满足它的端点中存在至少一个被选择的点。
下面的问题就转化成了求二分图的最小点覆盖问题,有一个结论:二分图的最小点覆盖等于二分图的最大匹配。 于是转而求这张图的最大匹配即可。
由于题目中的点数量级是105使用匈牙利增广路算法O(n2)复杂度妥妥超时。于是可以考虑使用最大流来解决这个问题。
使用dinic算法跑最大流复杂度是O(Nsqrt(N))
代码:
#include<iostream>
#include<queue>
#include<cstring>
#include<cstdio>
#include<map>
using namespace std;
const int N = 1e6 + 50;
const int M = 3e6 + 50;
const int inf = 1 << 30;
struct Edge{
int point;
int next;
int flow;
}nxt[N];
int head[N];
int dis[N];
bool vis[N];
int n,T,m1,m2,tot;
int s,t;
map<long long,int> mp1;
map<long long,int> mp2;
queue<int> q;
inline int getMap1(int x){return mp1.find(x)->second;}
inline int getMap2(int x){return mp2.find(x)->second;}
inline int min(int x,int y){return x < y ? x : y;}
bool bfs(){
memset(vis,false,sizeof(vis));
dis[s] = 0;
vis[s] = true;
q.push(s);
int k;
while(!q.empty()){
k = q.front();
q.pop();
for(int i = head[k];i;i = nxt[i].next){
if(vis[nxt[i].point] || !nxt[i].flow)
continue;
dis[nxt[i].point] = dis[k] + 1;
vis[nxt[i].point] = true;
q.push(nxt[i].point);
}
}
return vis[t];
}
int dfs(int k,int flow){
if(k == t || flow == 0){
return flow;
}
int sum = 0,f;
for(int i = head[k];i;i = nxt[i].next){
if(dis[nxt[i].point] == dis[k] + 1 && (f = dfs(nxt[i].point,min(nxt[i].flow,flow)))){
flow -= f;
sum += f;
nxt[i].flow -= f;
nxt[i ^ 1].flow += f;
}
if(!flow)
break;
}
return sum;
}
/*dinic算法*/
int dinic(){
int sum = 0;
while(bfs()){
sum += dfs(s,inf);
}
return sum;
}
void link(int x,int y,int f){
nxt[++tot] = {y,head[x],f};head[x] = tot;
nxt[++tot] = {x,head[y],0};head[y] = tot;
}
int main(){
for(cin >> T;T;T--){
scanf("%d",&n);
m1 = 1;
m2 = n + 10;
mp1.clear();
mp2.clear();
tot = 1;
s = 0;
t = 1;
/*建边的时候建议使用map映射一下x和y的值,它们是离散的,有负数且会很大,不方便处理*/
long long x,y;
while(n--){
scanf("%lld%lld",&x,&y);
x += y;
y = x - y * 2;
if(!mp1.count(x)){
mp1.insert(pair<long long,int>(x,++m1));
link(s,m1,1);
}
if(!mp2.count(y)){
mp2.insert(pair<long long,int>(y,++m2));
link(m2,t,1);
}
link(getMap1(x),getMap2(y),1);
}
cout << dinic() << endl;
for(int i = 0;i <= m2;i++) head[i] = 0;
}
}