一、背景知识
在ChatGPT引发全球关注之后，学习和运用大型语言模型迅速成为了热门趋势。作为程序员，我们不仅要理解其表象，更要探究其背后的原理。究竟是什么使得ChatGPT能够实现如此卓越的问答性能？自注意力机制的巧妙融入无疑是关键因素之一。那么，自注意力机制究竟是什么，它是如何创造出如此惊人的效果的呢？今天，就让我们共同探索这一机制背后的原理。
在亿万年的进化中，人类具备了快速关注环境中变化因素的能力，从而可以更好地趋利避害。这种能力就是注意力。在机器学习领域中，仿生学的理念也被广泛的使用。与神经网络、遗传算法相同，注意力机制在上世纪80年代，就已经在相关的研究中出现。在初期阶段，注意力机制常用于识别和提取图片中的关键信息。比如下图中，通过注意力算法提取图片中“停止指示牌”。
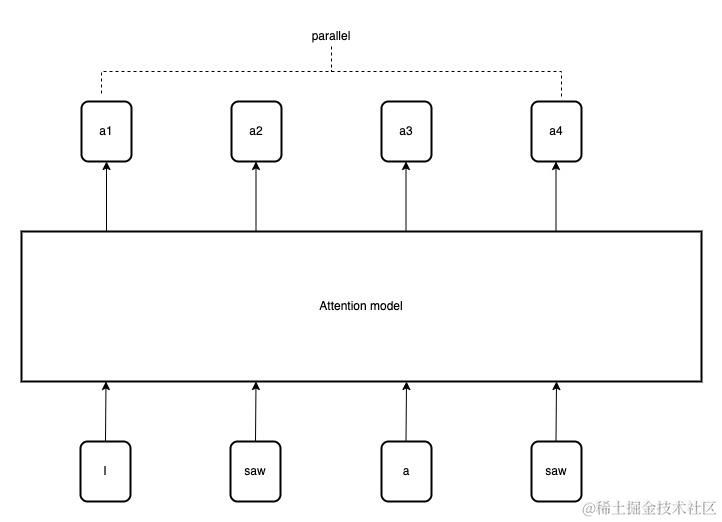
伴随深度学习算法的进步，在序列输入（Sequence Input）处理中，注意力机制也得到了较多的应用，其中比较有名的就属Transformer模型中的自注意力机制了。与无差别的对待每个顺序输入内容的算法相比，自注意力机制可以提取出输入内容间的相关性，因而取得了更好地结果表现。以词性分析为例，现在需要模型来分析句子中每个词的词性，输入的句子为“I saw a saw”。句子中出现了两个saw，第一个为动词，表示“看到了”的意思。而第二个为名词，表示“锯子”的意思。如果单独分析每个单词的词性，算法模型是无法判断此单词是名词还是动词。因此，必须要将两个词放入同一个上下文中分析，才可以得到预期的结果。我们通过设置窗口的方式，来获取连续上下文的效果。窗口的长度与计算的成本将成正相关。因此文本的长度越长，算法模型处理的资源消耗就越多。在大模型中，自注意力机制的引用，就是为了打破窗口长度与文本内容长度的相关性而设计的。
使用自注意力的模型可以直接计算出当前字符的结果，而不需要依赖前序内容的计算结果。这样可以保证计算的并行进行，并且不依赖窗口的限制。所以在处理超长序列内容时，其效率会有巨大的提升。
二、理解注意力机制（Attention mechanism）
注意力机制是模拟人的注意力的算法。可以将其理解成一个函数，可以用来计算两个向量的相关程度。如果两个向量相关程度越高，则注意力得分（Attention score）越高。如下图所示，是计算I向量在N向量上的注意力，I向量是由输入的第i个token进行词嵌入得来。N向量输入第n个token进行词嵌入得来。其O向量代表结果，是向量I在N上的注意力得分。在对O做处理后（比如多值时的Softmax处理），可以认为是I在输入N上的权重。经过注意力计算后，向量I与向量N的得分越高，则说明I与N的相关度越高。这样在后续的计算中，就可以只关注注意力得分高的向量关系，从而优化了计算效率。
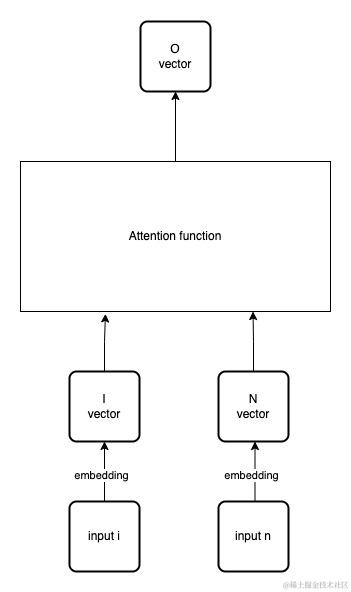
Attention function是一个确定的函数，在下一章节中会详细解释。简单的理解，在算法层面的注意力，就是两个向量的相似度计算。当两个向量相似度高时，此时输入向量的权重将更大，更抽象的讲，此时的输入向量将获得更多的注意力倾斜。
三、理解Self Attention
在Transformer框架（一种基于自注意力机制的深度学习模型）中，引用的注意力机制被称为自注意力机制（Self Attention，有时称为intra-attention）。这是在上一节介绍的基础上，对顺序输入内容进行了上下文相关的增强，使注意力机制可以更好的注意到整段输入内其他输入token的关联性信息，从而可以为提取更多信息创造条件。正是自注意力的作用，使得使用Transformer框架的GPT模型，在内容生成方面的效果出众。
如下图所示，输入是一组向量a1a4，输出为经过自注意力计算后的向量组b1b4。输入向量a1可能是一组原始的输入在经过词嵌入后，得到的向量。输入向量a1也可能是前序的某隐藏层的输出。换而言之，自注意力的计算结果，通常会作为其他层的输入，帮助模型的后续部分更好的理解输入向量组中，关联程度高的向量关系。
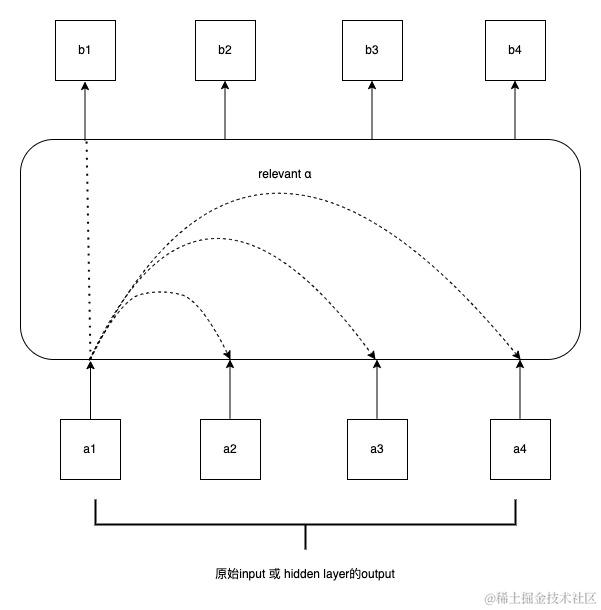
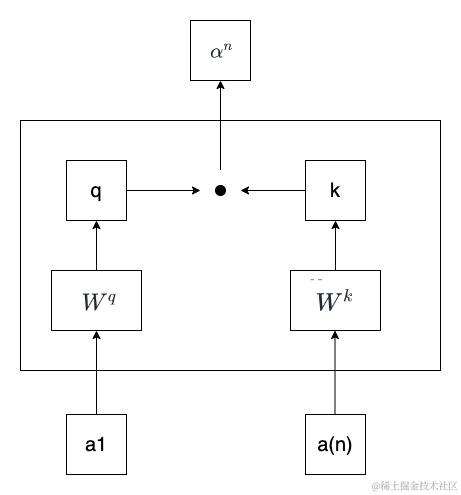
在上图中，输出向量b1是，输入向量a1经过考虑与所有输入向量的相关性（relevant）后，得到的结果。那么如何计算a1与a(n)的相关性α呢？这里就是上一章中提到的计算方式了。下面我们来看下，attention function中具体做了哪些计算。
首先，a1与
相乘得到向量q，a(n)与得到向量k。然后，再用向量q与k做点积（Dot Product）计算，得到a1与a(n)的相关性。整体过程如下图所示。其中，与是两个通过模型训练而学习得的矩阵，可以理解为确定的常量，其代表着注意力关注的重点（也可以理解为知识）。
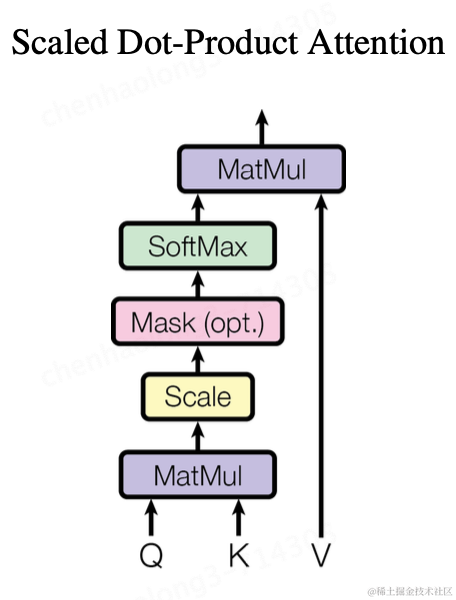
在attention function的选择上，并没有一个确定的公式。比如在Transformer中，就是使用了一种名为Scaled Dot-Product Attention的公式算法。因此，具体使用何种算法作为attention function，是一个开放性的问题，可以根据自己的理解，而尝试不同的算法。
下面我们来具体看下Transformer的Self Attention都做了哪些优化。在Self Attention中，注意力函数被抽象为，将Query信息与一个Key-Value数据集进行相关性计算的过程，计算的Output结果为Key-Value数据集中每对元素与Query的权重值。其中Query、Key、Value和Output均为向量。此函数被称为Scaled Dot-Product Attention。
让我们继续以a1-a4的输入为例，拆解一下Transformer中的Scaled Dot-Product Attention的计算过程。
1、将a1与
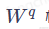相乘得到向量q1。
2、分别将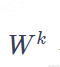
与a1、a2、a3、a4相乘，得到k1、k2、k3、k4。
3、分别将q1与k(n)点乘，得到
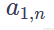
4、将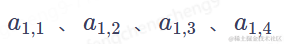
)进行softmax计算，得到
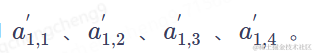)这里使用softmax是一个可替换的方案，也可以使用其他函数代替，比如ReLU。
5、分别将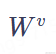
与a1、a2、a3、a4相乘，得到v1、v2、v3、v4。
6、最后 ，将v(n)乘以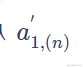
，得到矩阵b1。b2、b3、b4的计算过程同理，将输入的a1分别换成b2、b3、b4即可。
上述过程可以由下图描述得来。
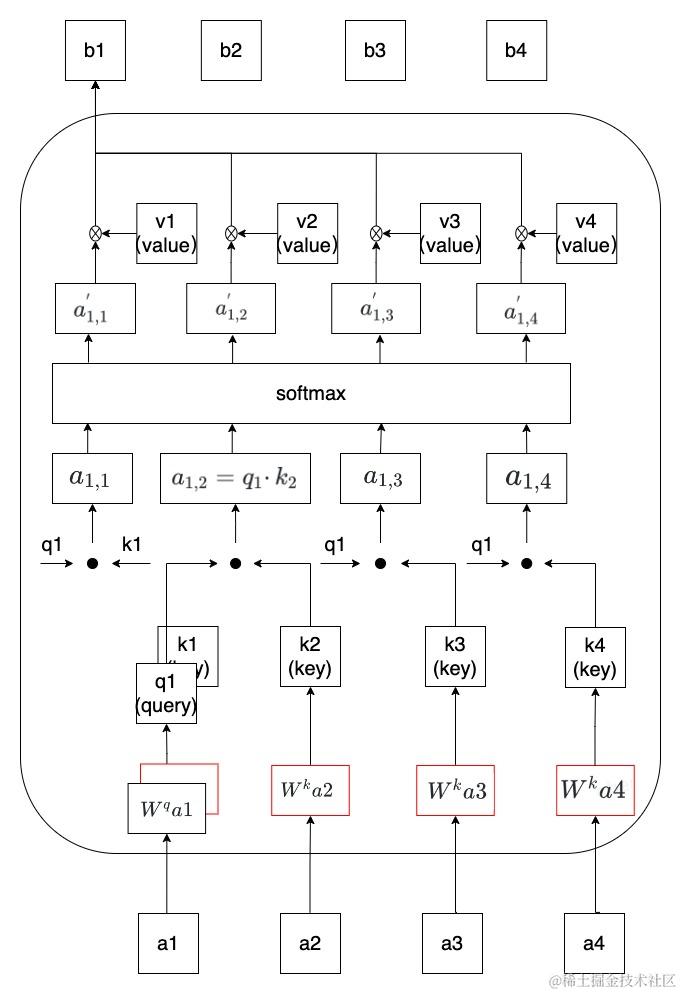
如果将a1、a2、a3、a4作为向量矩阵
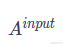)，一次性的输入到self-attention中。我们就可以得到对应的矩阵Q、K、V，即如下公式所示。其中
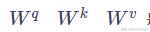是通过模型训练而学习到的常量系数。
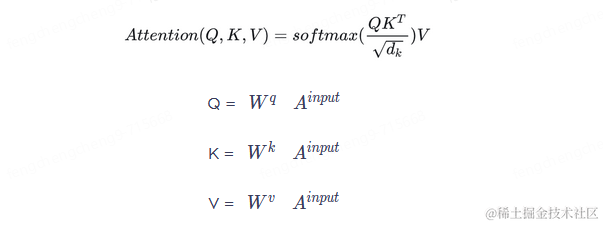
位置编码（Positional Encoding）
在上述的自注意力模型中，没有token对应的位置信息的输入。但是对于序列输入来讲，位置信息也包含了很重要的信息。比如之前的例子“I saw a saw”中，若去掉了位置信息，两个saw就无法判别具体是哪种含义。为了让Transformer模型关注到位置信息，模型设计者将位置进行了编码和向量化。这被成为了位置编码（Positional Encoding）。
模型设计者使用了sine、cosine函数，对位置进行编码，函数如下图。其中，pos代表当前位置，i代表维度。每个维度的位置预测都是一个正弦波，数值在
至之间。代表了词嵌入向量维度，使得生成的位置编码，可以使编码结果与词向量直接相加。
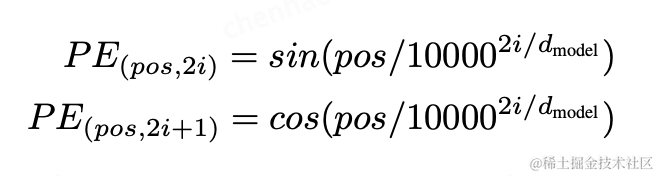
之所以选择在有限幅度循环震荡的sine、cosine函数进行位置编码，是为了让模型可以预测超过训练文本最大长度的内容。从而取得更好的泛化效果。
上述的位置编码函数，只是Transformer模型中使用的。编码函数的选择，也是一个暂无确定解的问题。模型的设计者，可以通过自身对位置的理解，而设计不同的位置编码函数。甚至在有一些论文中，已经使用模型训练的方式来动态生成位置编码信息。
四、理解Multi-head attention
Transformer架构为了能并行提取输入向量在不同维度的特征，在Self-attention的基础上，又提出了多头注意力（Multi-head attention）的概念。例如，在之前的训练中，模型分别学习了词性和句意两种维度的特征，分别记为
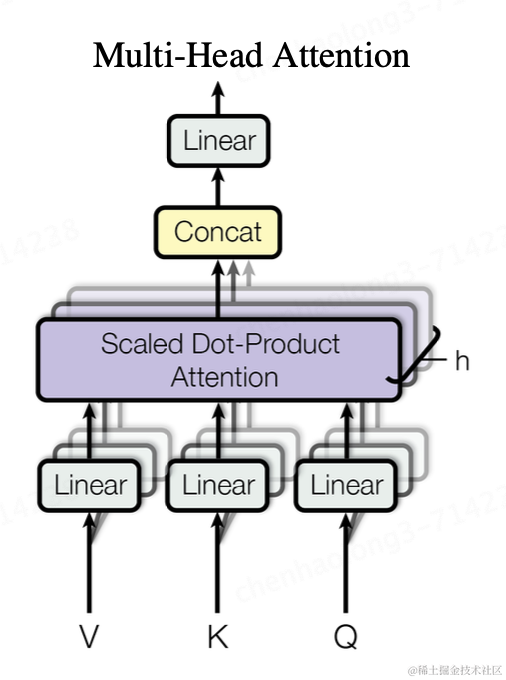
和，。这里就可以理解为由两个头（head）组成，分别用于提取不同注意力下的特征。多头注意力可以用下图表示，由h个头组成，分别用于计算不同的特征值。最后，由Concat方法，将特征进行合并，并送入下一层处理。
五、总结
自注意力概念首次在《Attention is all you need》这篇划时代的论文中被提出，标志着对注意力机制理解的一大突破。自注意力机制突破了传统注意力算法的性能局限，极大地提高了处理大规模数据集的效率。得益于此，模型在处理大数据集的训练效率主要取决于所投入的硬件资源，效果与之成正比。同时，自注意力机制的并行处理特性与GPU的并行计算能力相得益彰，进一步提升了训练的效率。因此，随着时间的流逝和对训练资源的持续投入，采用自注意力机制的大型语言模型在参数规模上也呈现出稳步的增长。
此外，本文只对与Transformer相关的自注意力机制做了介绍，而对比较经典的注意力机制介绍较少。但是了解注意力机制的发展过程，可以更好的帮助自注意力机制的理解。因此，推荐感兴趣的读者，读一下这篇专门介绍注意力机制发展史的论文《Attention Mechanism in Neural Networks: Where it Comes and Where it Goes》。
文章链接
BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding
NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE
Learning to Encode Position for Transformer with Continuous Dynamical Model
台大视频链接：
作者：京东物流 陈昊龙
来源：京东云开发者社区
