NumPy 泊松分布模拟与 Seaborn 可视化技巧

泊松分布

简介

泊松分布是一种离散概率分布，用于描述在给定时间间隔内随机事件发生的次数。它常用于模拟诸如客户到达商店、电话呼叫接入中心等事件。

参数

泊松分布用一个参数来定义：

λ：事件发生的平均速率，表示在单位时间内事件发生的平均次数。

公式

泊松分布的概率质量函数 (PMF) 给出了在指定时间间隔内发生 k 次事件的概率，计算公式为：

P(k) = e^(-λ) (λ^k) / k!

其中：

e^(-λ)：表示没有事件发生的概率。 (λ^k)：表示 k 次事件发生的概率。 k!：表示 k 个元素的阶乘，即 k × (k - 1) × (k - 2) × ... × 2 × 1。

生成泊松分布数据

NumPy 提供了 random.poisson() 函数来生成服从泊松分布的随机数。该函数接受以下参数：

lam：事件发生的平均速率。 size：输出数组的形状。

示例：生成一个平均速率为 5 的事件在 10 个时间间隔内发生的次数：

import numpy as np

data = np.random.poisson(lam=5, size=10)
print(data)

可视化泊松分布

Seaborn 库提供了便捷的函数来可视化分布，包括泊松分布。

示例：绘制平均速率为 7 的事件在 1000 个时间间隔内发生的次数分布：

import seaborn as sns
import numpy as np

data = np.random.poisson(lam=7, size=1000)
sns.distplot(data)
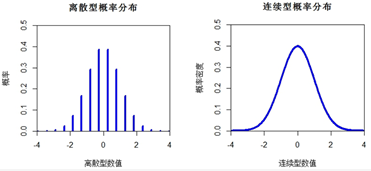
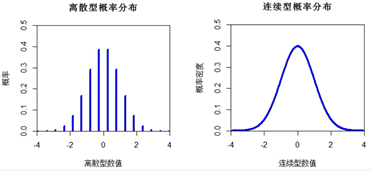
plt.show()

正态分布与泊松分布的关系

当事件发生的平均速率 λ 很大时，泊松分布可以近似为正态分布。其均值 μ 为 λ，标准差 σ 为 sqrt(λ)。

示例：比较泊松分布和正态分布的形状：

import seaborn as sns
import numpy as np

lam = 50

# 生成泊松分布数据
data_poisson = np.random.poisson(lam=lam, size=1000)

# 生成正态分布数据
mu = lam
sigma = np.sqrt(lam)
data_normal = np.random.normal(loc=mu, scale=sigma, size=1000)

sns.distplot(data_poisson, label="Poisson")
sns.distplot(data_normal, label="Normal")
plt.legend()
plt.show()

练习

在一个小时内，一家商店平均收到 10 位顾客。模拟顾客到达商店的次数并绘制分布图。
比较不同平均速率下泊松分布形状的变化。
利用泊松分布来模拟一个呼叫中心每天接到的电话呼叫数量，并计算平均呼叫量和每天接听超过 30 个电话的概率。

解决方案

import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt

# 1. 模拟顾客到达商店的次数并绘制分布图
data = np.random.poisson(lam=10, size=1000)
sns.distplot(data)
plt.show()

# 2. 比较不同平均速率下泊松分布形状的变化
lam_values = [5, 10, 20, 50]
for lam in lam_values:
    data = np.random.poisson(lam=lam, size=1000)
    sns.distplot(data, label=f"λ={lam}")
plt.legend()
plt.show()

# 3. 模拟电话呼叫数量并计算平均呼叫量和每天接听超过 30 个电话的概率
calls_per_day = np.random.poisson(lam=150, size=365)
print("平均呼叫量:", calls_per_day.mean())
print("每天接听超过 30 个电话的概率:", (calls_per_day > 30).mean())