文章目录
16. 数值的整数次方
题目链接
题目描述
解题思路
实现代码
16. 数值的整数次方
题目链接
NowCoder
题目描述
给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent,求 base 的 exponent 次方。
解题思路
下面的讨论中 x 代表 base,n 代表 exponent。
比如,我们求n的32次方,我们先知道n 的16次方,在16次方的基础上再平方就可以,同理,我们可以先求8次方,4次方,2次方,因此我们求32次方就变成了先求平方,在此基础上求4次方,再求8次方,再求16次方,最后就可以求得32次方。
我们提出如下的公式: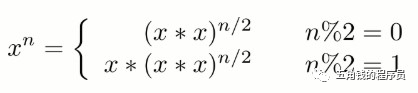
因为 (x*x)n/2 可以通过递归求解,并且每次递归 n 都减小一半,因此整个算法的时间复杂度为 O(logN)。
实现代码
package 数值的整数次方;/*作者 :XiangLin创建时间 :27/03/2020 17:00文件 :Solution.javaIDE :IntelliJ IDEA*/public class Solution { public double power(double base,int exponent){ if (exponent == 0) return 1; if (exponent == 1) return base; boolean isNagivate = false; if (exponent < 0){ isNagivate = true; exponent = -exponent; } double pow = power(base * base,exponent/2); if (exponent % 2 != 0){ pow = pow * base; } return isNagivate? 1 / pow : pow; } public static void main(String[] args) { Solution solution = new Solution(); System.out.println(solution.power(2.2,5)); }}

个人微信公众号,专注于学习资源、笔记分享,欢迎关注。我们一起成长,一起学习。一直纯真着,善良着,温情地热爱生活。
Don’t be in a hurry to grow up. Hold on to being a boy as long as you can.
不要急着长大,尽可能地做一个孩子吧。
本文分享自微信公众号 - 五角钱的程序员(xianglin965)。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。