::: tip 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度，记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2)，空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度，因为每次递归都要存储返回信息。 ::: 解题设计： ::: tip 算法设计的三个阶段： 第一阶段中，当节点数为奇数如a1到a7七个节点时，中间节点ppre指向a4，当节点数为偶数如a1到a6六个节点时，中间节点ppre指向a3。中间节点为分界线，将链表分为L1、L2两个链表。一般为了方便节点数为奇数时将中间节点划分到第一个链表L1中。 （双指针同时遍历是链表操作的常用场景。） 第二阶段中，链表的逆置不影响L2头节点。 第三阶段中，两个链表合并的操作可以当作是将L2链表插入进L1链表中。和头插法区别是L2链表中的节点已经有空间了，不需要在申请空间。 ::: 链表合并流程描述：组合后的新列表L以L1为基础，，L->next=L1->next即L指向的第一个节点为a1。pcur初始化指向第一个节点a1（此时L链表中只有一个节点a1，pcur指向新链表L的末尾节点即a1）。根据题意a1位置不变，p指向待放入节点的位置即L的a2，q指向L2的第一个节点，q指向的节点插入到L中的a2位置处时，pcur指向pcur的下一个节点a2（新链表尾部），q指向q的下一个节点。（新链表L中每添加一个节点，pcur都向后移动一个节点指向末尾）。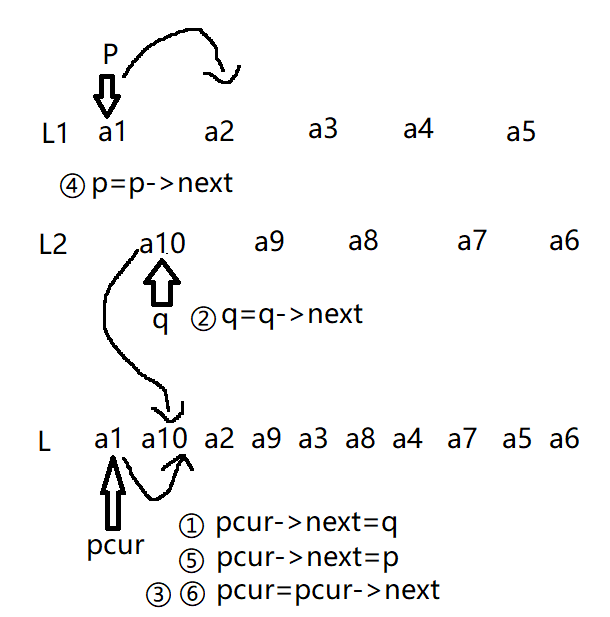 L独立出来如下图： 如上图a5是L1最后一个节点，p指向a5并放进L后，循环条件p!=NULL&&q!=NULL不成立，此时q指向a7，需要在循环外将q->next指向L2最后一个节点a6，然后pcur->next=q将a6放进L。 ::: tip 链表逆置的时间复杂度是O(n)，链表合并的空间复杂度为O(1)。 ::: 链表逆置 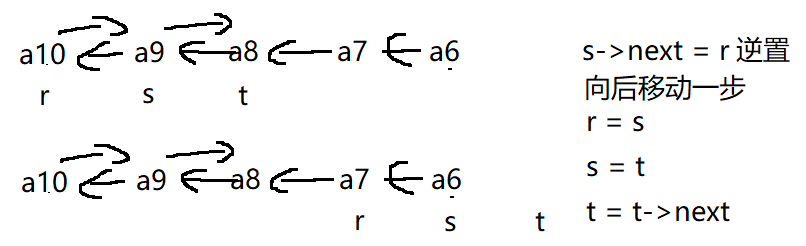全部代码如下：

#include <stdio.h>
#include <stdlib.h>

typedef struct node
{
    int data;
    struct node* next;
}NODE;
void insert_list(NODE*& L)
{
    L = (NODE*)malloc(sizeof(NODE));
    L->next = NULL;
    int x;
    scanf("%d", &x);
    NODE* s, * t;
    t = L;
    while (x != 9999)
    {
        s = (NODE*)malloc(sizeof(NODE));
        t->next = s;
        s->data = x;
        t = s;
        scanf("%d", &x);
    }
    t->next = NULL;
}
void find_mid(NODE* L, NODE*& L2)  //找到链表中间节点并设置好L2
{
    L2 = (NODE*)malloc(sizeof(NODE));  //为L2申请头节点
    NODE* pppre, * pcur;
    pppre = pcur = L->next;  //pppre指向中间节点，pcur指向最后一个节点
    while (pcur)  //循环到末尾时停止
    {
        pcur = pcur->next;
        //不能连续走两步，每走一步后需要判断是否来到链表尾部
        if (NULL == pcur)
        {
            break;
        }
        pcur = pcur->next;
        if (NULL == pcur)  //节点数为奇数时不需要这个判断，为偶数时需要，否则pppre会向下多走一步
        {
            break;
        }
        pppre = pppre->next;  //pcur可以成功向下走，则pppre也可以，不需要再做判断
    }
    //pppre指向中间节点，属于L链表的最后一个节点，pppre以后的节点属于L2链表
    L2->next = pppre->next;
    pppre->next = NULL;
}
void reverse(NODE*& L2)
{
    NODE* r, * s, * t;  //r、s、t分别指向L2的前三个节点
    r = L2->next;
    if (NULL == r)  //判断链表是否为空（没有节点）
    {
        return;
    }
    s = r->next;
    if (NULL == s)  //判断链表中是否只有一个节点
    {
        return;
    }
    t = s->next;
    while (t)  //t可以为空，t为空不影响其他指针
    //while(t)等同于while(t!=NULL)，表示节点t不存在，即t的数据域和指针域都不存在
    {
        s->next = r;  //节点逆置
        //三个指针同时向后走一步
        r = s;
        s = t;
        t = t->next;  
        //进入循环时已经确保节点t的存在，当t是最后一个节点t->next为NULL时，while循环跳出
    }
    s->next = r;
    L2->next->next = NULL;  //L2指向第一个节点，逆置后原来的第一个节点变为最后一个，指针域为空
    L2->next = s;  //此时链表的第一个节点变为s指向的节点，头节点的next指向链表第一个节点
}

void merge(NODE* L, NODE* L2)  //L和L2的两个头节点不变，不需要引用&
{
    NODE* pcur, * p, * q;
    pcur = L->next;  //pcur指向第一个节点
    p = pcur->next;  //p也可以指向pcur->next，即p从第二个节点开始加
    q = L2->next;
    while (q != NULL && p != NULL)  //while (q && p)
    {
        //pcur始终指向L的末尾，每次向L中放入一个节点，pcur都要向后走一步
        pcur->next = q;
        q = q->next;  //q用来遍历L2列表
        pcur = pcur->next;  
        pcur->next = p;  //p用来遍历L1列表
        p = p->next;
        pcur = pcur->next;
    }

    //两个链表中会有其一有剩余节点
    if (p==NULL)
    {
        pcur->next = q;
    }
    if(q==NULL)
    {
        pcur->next = p;
    }
    //或如下：
    //if (p != NULL)
    //{
    //    pcur->next = p;
    //}
    //if (q != NULL)
    //{
    //    pcur->next = q;
    //}
}

void print(NODE* L)
{
    L = L->next;
    while (L != NULL)
    {
        printf("%3d", L->data);
        L = L->next;
    }
    printf("\n");
}
int main()
{
    NODE* L;
    insert_list(L);
    print(L);
    NODE* L2 = NULL;
    find_mid(L, L2);  //L2指向中间节点
    reverse(L2);
    print(L2);
    merge(L, L2);
    free(L2);
    print(L);
    return 0;
}

所写代码的时间复杂度： 时间复杂度的分析重点是三个阶段写的三个子函数。 find_mid中的while循环条件是pcur!=NULL，pcur每次向后走两个节点，总的节点数为n时，while循环的次数是n/2，忽略首项系数1/2，时间复杂度为O(n)。 reverse中的while循环条件是t!=NULL，reverse逆置L2链表时对L2链表做遍历，L2链表中节点数为n/2，忽略首项系数1/2，时间复杂度为O(n)。 merge中的while循环条件是q!=NULL&&p!= NULL，p和q两条链表中节点数都为n/2，p和q遍历链表，循环遍历的次数为n/2，忽略首项系数1/2，时间复杂度为O(n)。 ::: warning 以上三个函数的总运行次数为n/2+n/2+n/2=1.5n，忽略首项系数1.5，整体时间复杂度为O(n)。 ::: ::: tip 时间复杂度不考虑代码的行数。 :::