CGAffineTransformMake(a,b,c,d,tx,ty)
a d 缩放, b c 旋转, tx ty 位移
(x , y) -> (x' , y') 的公式
x' = ax + cy + tx
y' = bx + dy + ty
矩阵的基本知识:
struct CGAffineTransform {
CGFloat a, b, c, d;
CGFloat tx, ty;
};
CGAffineTransform CGAffineTransformMake(CGFloat a, CGFloat b, CGFloat c, CGFloat d, CGFloat tx, CGFloat ty);
为了把二维图形的变化统一在一个坐标系里,引入了齐次坐标的概念,即把一个图形用一个三维矩阵表示,其中第三列总是(0,0,1),用来作为坐标系的标准。所以所有的变化都由前两列完成。
以上参数在矩阵中的表示为:
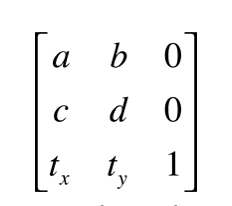
运算原理:原坐标设为(X,Y, 1)
| a b 0 |
(X,Y, 1) ⅹ | c d 0 | = (aX + cY + tx , bX + dY + ty , 1) ;
| tx ty 1 |
通过矩阵运算后的坐标(aX + cY + tx, bX + dY + ty, 1) 我们对比一下可知:
一、设a=d=1, b=c=0
(aX + cY + tx , bX + dY + ty , 1) = (X + tx , Y + ty , 1)
可见,这个时候,坐标是按照向量(tx,ty)进行平移,
也就是函数CGAffineTransform CGAffineMakeTranslation(CGFloat tx,CGFloat ty)的计算原理。
二、设b=c=tx=ty=0
(aX + cY + tx , bX + dY + ty , 1) = (aX , dY , 1)
可见,这个时候,坐标X按照a进行缩放,Y按照d进行缩放,a,d就是X,Y的比例系数,
也就是函数CGAffineTransform CGAffineTransformMakeScale(CGFloat sx, CGFloat sy)的计算原理。
a对应于sx,d对应于sy。
三、设tx=ty=0,a=cosβ,b=sinβ,c=-sinβ,d=cosβ
(aX + cY + tx , bX + dY + ty , 1) = (Xcosβ - Ysinβ , Xsinβ + Ycosβ , 1)
可见,这个时候,β就是旋转的角度,逆时针为正,顺时针为负。
也就是函数CGAffineTransform CGAffineTransformMakeRotation(CGFloat angle)的计算原理。
angle即β的弧度表示。
参考:







