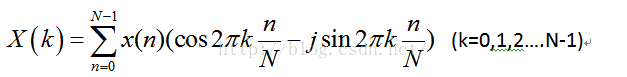利用离散傅立叶打造一个频谱app 先来look一下效果： 视频播放地址

来看一下离散傅立叶算法 这是我的，当然每个人的实现方式会一定偏差，主要是要依据傅立叶变化来。

                    int N = 16;
                    double PI = 3.1415926;
                    float[] real = new float[N];
                    float[] imag = new float[N];
                    for (int k = 0; k < N; k++) {
                        for (int n = 0; n < N; n++) {
                            real[k] = (float) (real[k] + buffer[n] * Math.cos(2 * PI * k * n / N));
                            imag[k] = (float) (imag[k] - buffer[n] * Math.sin(2 * PI * k * n / N));
                        }
                    }
                    float[] result = new float[real.length];
                    for (int i = 0; i < real.length; i++) {
                        result[i] = (float) Math.sqrt(real[i] * real[i] + imag[i] * imag[i]);
                    }

下面来介绍一下fft（快速傅立叶变化） DFT(DiscreteFourier Transform) 离散傅里叶变换 FFT（快速傅里叶变换）其本质就是DFT DFT(FFT)的作用:可以将信号从时域变换到频域，而且时域和频域都是离散的，通俗的说，可以求出一个信号由哪些正弦波叠加而成，求出的结果就是这些正弦波的幅度和相位，音乐播放器上面显示的就是音乐fft之后不同频率正弦波的幅度(所以你能看到不听的上下抖动). 那么为什么可以求出正弦波的幅度呢，我们也可以利用信号的相关性检测信号波中是否含有某个频率的信号波：把一个待检测信号波乘以另一个信号波，再把这个新的信号波所有的点进行相加，从相加的结果就可以判断出这两个信号的相似程度. 差不多了，理论我们就了解下。直接来应用。 DFT的公式：

android 音乐频谱APP实现： 第一种实现思路：我们利用AudioRecord去录音，然后读取，然后把读取出来的数组dft运算，得到我们最后需要个result结果，最后把result结果写一个自定义控件就可以。 第二种实现思路：我们利用AudioRecord+audioTrack+Visualizer的方式去实现整个从录音到dft运算到过程。AudioRecord负责获取外部声音，audioTrack负责将录制到声音播放，Visualizer负责进行dft运算。Visualizer是google提供到微型可视化音乐工具。你不需要去考虑如何实现dft算法。

当然具体使用哪种方法你需要自己选择。前者的可控性更强一些。作者俩种都帮你试过了，最后dft以后得到都数据展示都效果都是相似可以接受的。 audioTrack针对这个需要声明的是如果你的app需要实现语音通话则必须先考虑一下这个组件，这组件的功能都是为了边录边播放。