一、简介:
1.1、字典树trie:
字典树trie 搜索关键码的时间和关键码自身及其长度有关,最快是0(1),,即在第一层即可判断是否搜索到,最坏的情况是0(n), n为Trie树的层数。由于很多时候Trie树的大多数结点分支很少,因此Trie树结构空间浪费比较多。
关键码检索策略可以根据关键码是否可以动态变化,分为两类:
1、动态策略"dynamic method": 允许检索表动态变化,包括hashing,二进制树,B+树,扩展hashing,trie hashing;
2、静态策略"static method": 不允许检索表动态变化,包括完美hashing,稀疏表,压缩trie;
本文介绍的double array trie 在两种策略之间,称为"weak static method";
1.2、Digital-search Tree定义:
K 表示模式串(KEYS)集合.
S 是有限的节点集合.
s 是初始节点,即root节点.
I 表示有限的输入字符(INPUT)集合.
g() 转移函数,是一个节点在接受一个字符后转向另一个节点或者失败的函数.
A 表示有限的接受状态(ACCEPT)节点集合.
这里只用到DS tree 的定义,其具体实现不需要理解, 该定义同前面的有限自动机(FSM)定义类似,仅为了后面理解方便;同FSM 中把字符直接作为边的做法不同,这里需要把所有关键码(如字符)转换成对应数字,用作数组索引的一个偏移.
*这里为了区别带有相同前缀的模式串如"the"和"then",在每个模式串末尾加上特定符号'#'(可根据实际情况变换);
假设一个模式串集K, 节点s,节点m 满足 g(s,a) = m:
1.3、DAT(double-array trie)定义:
把trie压缩成两个一维数组 BASE,CHECK 的DS-Tree(digital search tree)算法,称为double-array trie(下面缩写成DAT);这个算法的本质就是将Trie树结构简化为两个线性数组.
1.4、DAT由triple-array 演化而来缘由:
triple-array 结构较之DAT多了个 NEXT 数组,因我们可以把输入字符用数字化表示,
有 BASE[s] + a = m 以及CHECK[m] = s;
可知下一个节点m可以通过当前节点加上当前输入字符的索引算得出,并且保证其上一个节点就是s,故triple-array结构可以压缩到两个数组;
1.5、reduced trie :
reduced trie 是在DAT基础上,引进TAIL[] 数组优化而来, 介绍reduced trie之前解释下几个名词:
1>、独立节点(separate node):
当字符'a'(或对应的边)能绝对把当前模式串区分于别的模式串,节点 m 称为独立节点(separate node).
2>、独立字符串(a single string for m):
从独立节点m 到模式串末尾的残留字符串称为单独节点m的独立字符串,标记为 STR[m].
3>、the tail of K:
模式串 K 的独立字符串会从模式串中剪切掉存储到 TAIL[],记为the tail of K.
4>、reduced trie的定义:
一棵树只由从 root 节点到 独立节点 的边构造,则称为reduced trie.
下面是一个reduced trie 例子:
对于关键码集 K={baby#, bachelor#, badge#, jar#}, reduced trie 最后reduced trie构造如下(图一):
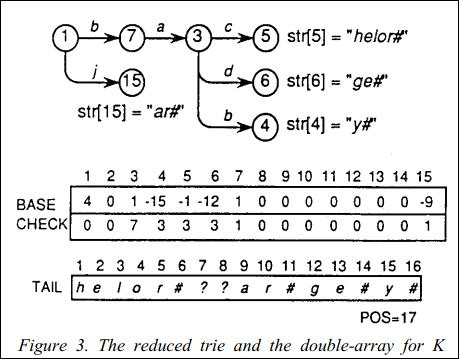
以上图为例,reduced trie 有如下两个关系:
关系1、如果在 reduced trie中有一条边满足 g(s,a)=m, 则有:
BASE[s] + a = m, and CHECK[m] = s.(本文假定对应边上的标签: '#'= 1,'a'=2,'b'=3,'d'=4...以此类推)
*在实际的编码需要考虑各字符对应的数值编码,我下面的代码为了模拟本文的结果,做了对应调整;
关系2、已知m是一个独立节点,以及其独立字符串 STR[m] = b1 b2...bh,则有:
a> BASE[m] < 0;
b> 假定 p = -BASE[m], 则有 TAIL[p]= b1, TAIL[p + 1]= b2, TAIL[p + h + 1]= bh.
*这两个关系对理解 reduced trie 比较重要,在后续原理讲解以及code中均有体现;
二、Reduced Trie 检索,构造,删除具体流程:
2.1、Reduced Trie 的检索:
以检索关键码 "bachelor#"为例:
step 1: 将root 节点存储在BASE[1]位置,从root节点开始,首字符'b'对应数值为3,根据上面关系1有:
BASE[s] + a = BASE[1]+ 'b' = BASE[l]+3 = 4+3 = 7
同时有 CHECK[7] = 1
step 2:注意到上面得出的 BASE 索引值7 为正数,同时根据下一个字符'a'对应数值为2,有:
BASE[7] + 'a'= BASE[7] + 2 = l + 2 = 3,
同时有 CHECK[3] = 7
step 3,4:重复以上步骤,根据字符'c'对应数字4:
BASE[3]+ 'c' = BASE[3] + 4 = 1 + 4 = 5,
同时有 CHECK[5] = 3
step 5: 已知 BASE[5] 的值为 –1. 负数表明剩余的 独立字符串 存储在起始位置为 -BASE[5] = 1 的TAIL数组 中,其他关键码的检索同以上过程,注意每次检索开始都是从root节点开始;
注意到上面检索过程只涉及到数组直接的查找,以及加法运算,可知检索算法非常的高效;
2.2、Reduced Trie 的插入(构造):
插入(构造)又分四种情况:
case 1:当双数组trie 为空时,插入关键码;
case 2:在没有冲突时插入关键码;
case 3:当插入关键码时有冲突,这时新增字符必须添加进 BASE,同时将对应 独立字符串 从TAIL 中移除、修改以便解决冲突; 但是不需要移动 BASE 数组中原有值;
case 4:同case3 当插入关键码时有冲突,不同的是这时需要移动 BASE 中原有值,以便能解决冲突;
发生冲突说明 两个不同的字符在BASE、CHECK 中有相同的索引值,四种情况分别以插入"bachelor#"(case 1),"jar#"case 2),"badge#"case 3),"baby#"case 4)为例,并配以图示;
下面是详细过程:
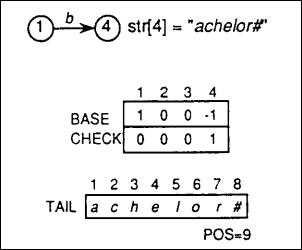
case 1:当双数组trie 为空时,插入关键码,以插入"bachelor#"为例:
Step 1:从root 节点 BASE[1] 开始, 'b'对应数字3:
BASE[1] + 'b' = BASE[l] + 3 = l + 3 = 4, and CHECK[4] = 0 ≠ 1
Step 2:上面求出的CHECK[4] = 0 表明该节点 BASE[4] 为独立节点,同时直接记录剩余的 独立字符串 "achelor#" 至TAIL[]中;
Step 3:设置:
BASE[4] = -tail_pos = -1;(tail_pos 初始为1, TAIL[0]不存储)
表明剩余的 独立字符串 存储在TAIL[] 起始位置为 tail_pos;同时设置:
CHECK[4] = 1;
表明节点4 的父节点是节点1;
Step 4:在把独立字符串"achelor#"拷贝进 TAIL[] 后, 更新 TAIL 空闲索引值:
tail_pos = 9;
表明 TAIL[] 数组下次允许插入位置;
同时下图是插入"bachelor#" 后 reduced trie 结构以及各数组数据的图示(图二):
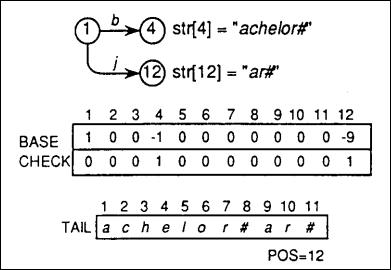
case 2:在没有冲突时插入关键码,以插入"jar#"为例:
Step 1:同样从root节点开始,即BASE[1],'j'对应数字11,有:
BASE[l] + 'j' = BASE[1]+11 = 1+11 = 12, and CHECK [12]= 0 ≠ 1
Step 2:CHECK[12] = 0 表明该节点BASE[12]为独立节点,不会和已有节点冲突,可以直接记录剩余的 独立字符串 "r#" 至 TAIL[] 尾部;
Step 3:设置
BASE[12] = -tail_pos = -9;
表明该节点后续的 独立字符串"r#"存储以 TAIL[9] 开始的后面数组中,同时设置:
CHECK[12] = 1;
表明节点12 的父节点是节点1;
Step 4:在把独立字符串"r#"拷贝进 TAIL[] 后, 更新 TAIL 空闲索引值:
tail_pos = 12;
表明 TAIL[] 数组下次允许插入位置;
通过观察得知,case 2 和 case 1没有本质区别;下图是插入"jar#" 后 reduced trie 结构以及各数组数据的图示(图三):
在讲解case3、4之前,先引入一个函数 X_CHECK(list),函数返回正数q,其中q满足
1、q > 0;
2、对于字符串list中所有字符'c'有,CHECK[q+c] = 0;
q 是从1开始确认,并每次递增1,该函数本质是在BASE[]数组中发生冲突时,找到最近一个基准位置,确保有足够空间能保存所有冲突(重叠)的节点;
case 3:当插入关键码时有冲突,这时新增字符必须添加进 BASE,同时将对应 独立字符串 从TAIL 中移除、修改以便解决冲突; 但是不需要移动 BASE 数组中原有值,这里以插入"badge#"为例:
Step 1:同样从root节点开始,即BASE[1],'j'对应数字11:
BASE[l] + 'b' = BASE [l]+3 = l+3= 4, 已有 CHECK[4] = 1
上面CHECK[4] = 1 非0,表明从 节点1 到节点4 的有向边已经存在;
Step 2:利用上面求出的数值4,知道 BASE[] 数组 对应位置数值:
BASE[4] = -1;
BASE[4] 位置的负数表明该节点是独立节点,以及剩余的独立字符串存储在TAIL 中,现在新的关键码有同样的节点,说明原来该节点不能作为新的独立节点,即原来独立字符串中有字符需要存储到BASE 中,同时需要修改TAIL 中存储的对应 独立字符串;
Step 3:从-BASE[4]位置开始检索读取存储在 TAIL[] 的独立字符串, 和新插入关键码后续字符比对,即比对“chelor#”和"dge#",两者不相等,说明不是同一个关键码,接下来存储两者的最大公共前缀,以及两者各自剩余的独立字符串;
Step 4:保存下原来独立字符串起始位置:
TEMP = -BASE[4] = 1;
Step 5:已知"adge#" and "achelor#" 两者最大公共前缀"a", 通过 X_CHECK({'a'})求出新基节点:
CHECK[ q+a ]= CHECK [ l+'a' ] = CHECK[ l+2 ]= CHECK[3] = 0
可知当 q=1 满足条件,同时是BASE[4]的新值,以及CHECK[3]=0 表明新基节点3为空;
Step 6:BASE[4] 赋新值:
BASE[4] = q = 1;
同时赋予上面节点3 对应 CHECK 值;
CHECK[ BASE[4]+'a'] = CHECK[l+2] = CHECK [3] = 4;
容易得知节点3 的父节点是节点 4;
注意:本例这里步骤5、6不需要重复执行,如果公共前缀不止一个字符,则需要重复多次,次数为公共前缀字符长度;
Step 7:接下来存储两个关键码剩余的字符串 "chelor#","dge#", 通过X_CHECK({'c','d'})计算,存储基于BASE[3]节点的两条外向边'c','d'对应节点 的基索引值,如下:
For 'c': CHECK[q + 'c'] = CHECK[l + 4] = CHECK[5] = 0;
For 'd': CHECK[q + 'd'] = CHECK[l + 5] = CHECK[6] = 0;
可以知道节点5、6均空闲,所以q = 1 满足条件,所以设置:
BASE[3] = 1;
Step 8:计算"chelor#" 的独立节点字符'c' 以及剩余独立字符串在BASE 以及CHECK[] 对应数值:
BASE[3] + 'c' = 1+4 = 5;
BASE[5] = -TEMP = –1;
CHECK[5] = 3;
BASE[] 中的值为正时解释当前节点所有子节点的基准值,为负时解释独立字符串在TAIL 中的位置;
CHECK[] 中的值表明节点5节点父节点是3,解释各节点的层次关系;
同时图示中各节点的数值为其 父节点基准值 和 至该节点外向边字符索引值 之和;
Step 9:把上面剩余的 独立字符串 "helor#" 存储到TAIL 中, 起始地址为-CHECK[5] = 1,根据以下图示,TAIL[7] TAIL[8] 处字符变成'?'表明无效数据;(我的代码里面没有做这个处理,读者可以自己实现下);
Step 10:接下来存储 另一个字符串"dge#':
BASE[3] +‘d’= l + 5 = 6;
BASE[6] = -tail_pos = –12;
CHECK[6] = 3;
同时把 独立字符串 "ge#' 存储到 TAIL[12] 位置;
Step 11:最后更新TAIL[] 空闲索引值为 插入"ge#" 后的位置:
tail_pos = 12 + length["ge#"] = 12 + 3 = 15;
总结:当新增关键码和已有关键码 因有相同前缀 导致冲突,需要已经存储进TAIL[] 的独立字符串 提取出来比对,把公共前缀字符 存储进BASE[] CHECK[] 中,依次根据上一个节点求下一个节点存储位置,并根据最后一个公共节点 BASE 值和独立字符索引,存储对应独立节点,同时独立节点BASE[] 值 关联对应独立字符串 在TAIL[]位置; 下图是case 3 插入结束后的数据图(图四):

case 4:同case3 当插入关键码时有冲突,不同的是这时需要移动 BASE 中原有值,以便能解决冲突,以插入"baby#"为例:
Step 1:同样从root节点开始,依据前面解释,可以遍历前三个字符:
BASE[l] + 'b' = BASE[l]+3 = l+3= 4, and CHECK[4] = 1;
BASE[4] + 'a' = BASE[4]+2 = l+2= 3, and CHECK[3] = 4;
BASE[3] + 'b' = BASE[3]+3 = l+3= 4, and CHECK[4] = l ≠ 3;
CHECK[4] 位置的不一致, 表明节点1 和 节点3 有冲突,需要修改以便允许后续字符插入;
Step 2:保存一个临时变量:
EMP_NODE1 = BASE[3] + 'b' = 1 + 3 = 4;
假如CHECK[4]是为0,则表明该节点空闲,可以直接插入TAIL[] 的tail_pos位置;但实际不是,需如下处理:
Step 3:将上面发生冲突节点的各外向变对应字符,存储在以冲突的节点数值号(3)为序号的 (char *)LIST[] 对应位置中,有:
LIST[3] = {'c','d'};
另一个list,以step 1 中 CHECK 算出的冲突节点号 1 为序号,并把所有该节点的外向变对应的字符,存储到(char *)LIST[] 对应位置中:
LIST[1] = {'b','j'};
Step 4:现在的目的是要把新字符串 关联到 节点3处,比较这两个 LIST 长度,其中LIST[3] 做加1处理,因考虑到在节点3处需新增关联字符.关系式如下:
compare( length(LlST[3]) + 1, length(LIST[l]) ) = compare(3, 2)
如果length(LIST[3])+1 < length(LIST[1]),则节点3需要修改;但现在正好相反,则需要修改节点1,具体如下;
Step 5:把上面需要修改的节点对应 BASE 值存储到一个临时变量中:
TEMP_BASE = BASE[l] = l;
计算出一个能保存LIST[1]所有字符,且距离最近的有效 BASE 基值,计算如下:
X_CHECK['b'] : CHECK[q+'b']
= CHECK[1+3] = CHECK[4] = l ≠ 0;
CHECK[2+3] = CHECK[5] = –l ≠ 0;
CHECK[3+3] = CHECK[6] =–12 ≠ 0;
CHECK[4+3] = CHECK[7] = 0 (available)
同时有:
X_CHECK['j']: CHECK[q+'j'] = CHECK[4+11] = CHECK[15] ≠ 0 (available)
可知当 q = 4 是可行的,设置新 BASE 值:
BASE[1] = 4;
Step 6:对于字符'b',将该节点各值存储至临时变量:
TEMP_NODE1 = TEMP_BASE + 'b' = 1 + 3 = 4;
TEMP_NODE2 = BASE[1] + 'b' = 4 + 3 = 7;
首先把原来节点的 BASE 值赋值到新节点:
BASE[TEMP_NODE2] = BASE[TEMP_NODE1]; 即: BASE[7] = BASE[4] = 1;
同时设置新节点的CHECK 值:
CHECK[TEMP_NODE2] = CHECK[7] = CHECK[4] = 1;
Step 7:因有:
BASE[TEMP_NODE1] = BASE[4] = 1 > 0;
可知,该节点作为基准值,而不是指向TAIL 存储位置,所以需要把所有以该节点为基准值的节点 关联到新节点,即遍历从该节点基准值后所有节点是否其父节点为原来节点:
CHECK[ BASE[TEMP_NODE1] + w ] = TEMP_NODE1;
即查找所有满足下式的 w 偏移值:
CHECK[ BASE[4]+ w ] = 4;
CHECK[1+ w ] = 4;
可知只有 w = 2 (字符'a')满足条件;
同时修改对应CHECK 值指向 新节点,有:
CHECK[ BASE[4] + w ] = CHECK[ l+2 ] = CHECK[3] = TEMP_NODE2 = 7;
Step 8:初始化字符'b'对应节点(图四中的节点4)的BASE 值 以及CHECK 值:
BASE [ TEMP_NODE1 ] = BASE [4] = 0;
CHECK [ TEMP_NODE1 ] = CHECK [4] = 0;
Step 9:前面移动了字符'b'对应的节点4,接下来移动字符'j'对应节点12,类似的,将该节点各值存储至临时变量:
TEMP_NODE1 = TEMP_BASE + 'j' = 1+11 = 12;
TEMP_NODE2 = BASE[1] + 'j' = 4+11 = 15;
首先把原来节点的 BASE 值赋值到新节点:
BASE[ TEMP_NODE2] = BASE[ TEMP_NODE1 ]; 即 BASE[15] = BASE[12]= -9;
同时修改对应CHECK 值指向 新节点,有:
CHECK[ TEMP_NODE2 ] = CHECK[15] = CHECK[12] = 1;
Step 10:和前面节点4 BASE 值为正不同:
BASE[ TEMP_NODE1 ] = BASE[12] = –9 < 0;
表明该节点为独立节点,及其后面后缀存储在TAIL 数组中;只需要初始化原来节点12 BASE 及 CHECK 值:
BASE [ TEMP_NODE1 ] = BASE [12] = 0;
CHECK [ TEMP_NODE1 ] = CHECK [12 ] = 0;
至此,baby 中'b'插入导致的冲突已经解决了,下面只需存储剩余字符串"by#"就行了;
Step 11:下面考虑下原来 没修改的节点3(图四),在其后面插入新节点ba'b'y中第二个'b':
TEMP_NODE = BASE[3] + 'b' = 1+3 = 4;
Step 12:并将新节点BASE 值 指向独立字符串存储 位置:
BASE [ TEMP_NODE ] =BASE [4] = –tail_pos =–15;
同时设置该独立节点CHECK值:
CHECK[ TEMP_NODE ] = CHECK[4] = 3;
Step 13:插入对应独立字符串至 TAIL[] tail_pos位置:
TAlL[ tail_pos ] = TAlL[15] + "y#";
Step 14:更新TAIL[] 数组最新位置值:
tail_pos = tail_pos + length["y#"] = 15+2 = 17;
总结:当插入发送冲突时,如果BASE 数组值必须修改以便能够正常存储新插入字符时;需要比较发送冲突的节点 和 原来节点 各自分支数,移动分支较少的"轴点" 至新位置以便插入新节点;如case 4中 需要比较
节点1 分支"b,j" 和 节点3 分支"c, d ,b" ,故需移动节点1 的两个子节点;
2.3、Reduced Trie 的删除:
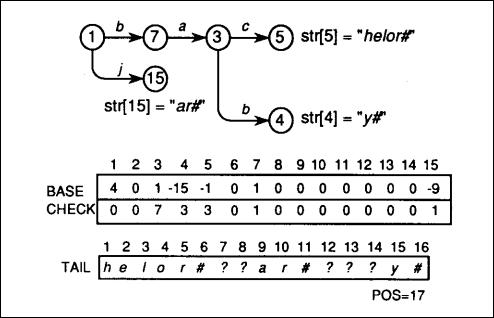
从双数组tire 中删除节点也是直接了当的,删除操作 和插入 case 2 中遍历处理过程类似.实际上,唯一的区别是需要重置指向 删除了的 关键字 存储在TAIL[]中的指针;这里以删除"badge#"为例:
step 1:同样从root节点开始,即BASE[1],对于关键字"badge"各字符BASE[] CHECK[] 值如下:
BASE[1] + 'b' = BASE[1]+3 = 4+3=7, and CHECK[7] = 1;
BASE[7] + 'a' = BASE[7]+2 = l+2=3, and CHECK[3] = 7;
BASE[3] + 'd' = BASE[3]+5 = l+5=6, and CHECK[6] = 3;
BASE[6] = –12 < 0; 表明为 separate node.
step 2:比较剩余字符串"ge#" 和 存储在TAIL -BASE[6] 即12位置的字符串:
compare("ge#", "ge#");
step 3:对应字符串相等,所以重置对应指向TAIL[] 的指针,即:
BASE [6] = 0;
CHECK [6] = 0;
下图(图五)为删除"badge"后结果图:
完整 code 我放在GitHub,ReadMe.txt里面有具体测试输入介绍;
https://github.com/oncelife/double-array-trie/
三、后记:
本文大部分从PDF 翻译过来,但是很多地方加上了我个人理解,也是我开始觉得不好理解,难理解的地方;
后续可以优化的有:
1、算法结构优化;
2、增加对中文支持等;
最近时间较忙,致使断断续续几经拖延才完成,本文如有任何问题,还请不吝赐教;
reference:
http://zh.wikipedia.org/zh-cn/Trie
An Implementation of Double-Array Trie.pdf
http://linux.thai.net/~thep/datrie/datrie.html
An Efficient Digital Search Algorithm by Using a Double-Array Structure.pdf















