问：Error和Exception的区别？

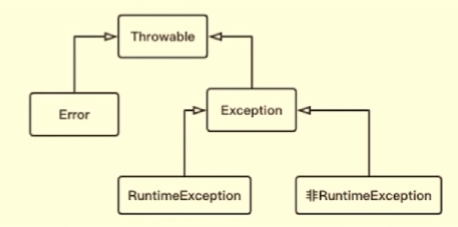
ps：Throwable上层是Object

• Error：程序无法处理的系统错误，编译器不做检查
• Exception：程序可以处理的异常，捕获后可能恢复

RuntimeException：不可预知的，程序应当自行避免（比如加入if(name!=null)）

非RuntimeException：可预知的，从编译器校验的异常

从责任角度看：

1. Error属于JVM需要负担的责任
2. RuntimeException是程序应该负担的责任
3. CheckedException可检查异常是java编译器应该负担的责任

RuntimeException常见的异常:

1. NullPointerException - 空指针引用异常
2. ClassCastException - 类型强制转换异常
3. IllegalArgumentException - 传递非法参数异常
4. IndexOutOfBoundsException - 下标越界异常
5. NumberFormatException - 数字格式异常
6. ArithmeticException - 算术运算异常
7. ArrayStoreException - 向数组中存放与声明类型不兼容对象异常
8. NegativeArraySizeException - 创建一个大小为负数的数组错误异常
9. SecurityException - 安全异常
10. UnsupportedOperationException - 不支持的操作异常

 

非RuntimeException常见异常：

1. ClassNotFoundException 找不到指定class的异常
2. IOexception IO操作异常
3. FileNotFoundException 找不到指定文件的异常

Error常见的异常：

1. NoClassDefFoundError 找不到class定义的异常（class或jar不存在、类文件存在但是在不同的域中、大小写问题，javac无视大小写）
2. StackOverflowError 深递归导致栈被消耗尽而抛出的异常
3. OutOfMemoryError 内存溢出异常

数据结构考点：

1. 数组和链表的区别
2. 链表的操作，如反转、链表环路检测、双向链表、循环链表相关操作
3. 队列、栈的应用
4. 二叉树的遍历方式（前序中序后序）以及递归和非递归的实现
5. 红黑树旋转

算法考点：

1. 内部排序：如递归排序、交换排序（冒泡、快排）、选择排序、插入排序
2. 外部排序：应掌握如何利用有限的内存配合海量的歪脖存储来处理超大的数据集，写不出来也要有相关思路（归并排序）

算法常问的问题：

1. 哪些排序是不稳定的，稳定意味着什么？（快排、堆排）
2. 不同数据量级，各种排序最好或者最差的情况（算法的时间、空间复杂度）
3. 如何优化算法（空间换时间）

java集合框架 主要集中在java.util包中 其中最关键的是juc包

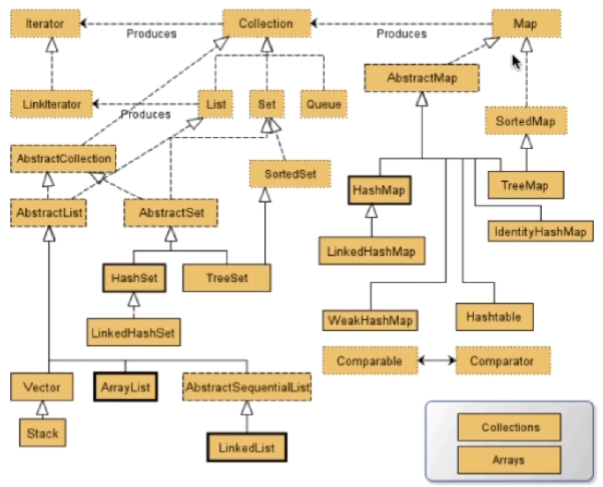
集合中set和list：

总结就是：

1. list：有序可重复（可通过索引直接查找元素）
   1. 底层是数组ArrayList和Vector。查找第n个数据时间复杂度是O(1)，插入或者删除时间复杂度是O(N)，在数组的任意位置插入或者删除，后面的数据都要移动（最好的情况是O(1)最坏O(N)），所以总体的时间复杂度仍然是O(N)
   2. 底层是链表 LinkedList。在链表中查找第n个数据的时间复杂度是 O(N)，但是插入和删除数据的时间复杂度是O(1) ，因为只要改指针就行了
2. list：无序不重复（查找只能通过遍历整个集合）
   1. 底层是hashMap的hashSet 时间复杂度为O(1)  
   2. 底层是二叉树 TreeSet 时间复杂度为O(log(n))

常用数据结构的时间复杂度:

Data Structure

Add

Find

Delete

GetByIndex

Array (T[])

O(n)

O(n)

O(n)

O(1)

Linked list (LinkedList)

O(1)

O(n)

O(n)

O(n)

Resizable array list (List)

O(1)

O(n)

O(n)

O(1)

Stack (Stack)

O(1)

-

O(1)

-

Queue (Queue)

O(1)

-

O(1)

-

Hash table (Dictionary<K,T>)

O(1)

O(1)

O(1)

-

Tree-based dictionary(SortedDictionary<K,T>)

O(log n)

O(log n)

O(log n)

-

Hash table based set (HashSet)

O(1)

O(1)

O(1)

-

Tree based set (SortedSet)

O(log n)

O(log n)

O(log n)

-