学更好的别人,
做更好的自己。
——《微卡智享》
本文长度为4379字,预计阅读11分钟
前言
前一篇《 C++ OpenCV透视变换综合练习》中针对透视变换做了一个小练习,上篇中我们用多边形拟合的点集来计算离最小旋转矩形最近的点来定义为透视变换的点,效果是有,无意间又想了一个新的思路,在原来的点的基础上效果会更好一点,其中就用到了直线拟合的方法,今天这篇就说一下优化的思路及直线拟合的函数。

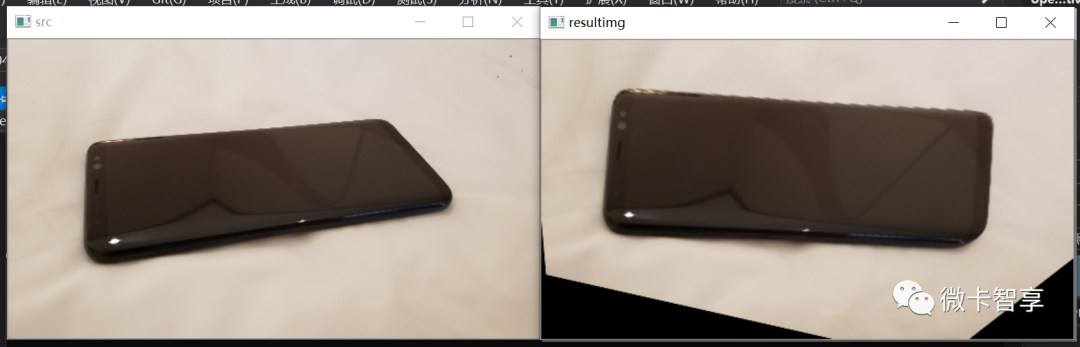
实现效果

放大图
直线拟合函数
微卡智享
void cv::fitLine(
参数说明:
points: 用于拟合直线的输入点集,可以是二维点的cv::Mat数组,也可以是二维点的STL vector。
line: 输出的直线,对于二维直线而言类型为cv::Vec4f,对于三维直线类型则是cv::Vec6f,输出参数的前半部分给出的是直线的方向,而后半部分给出的是直线上的一点(即通常所说的点斜式直线)。
distType: 距离类型,拟合直线时,要使输入点到拟合直线的距离和最小化(即下面公式中的cost最小化),可供选的距离类型如下表所示,ri表示的是输入的点到直线的距离。
CV_DIST_USER =-1, /* User defined distance */
param:距离参数,跟所选的距离类型有关,值可以设置为0,cv::fitLine()函数本身会自动选择最优化的值。
reps:拟合直线所需要的径向精度,一般设置为0.01或1e-2。
**aeps:**拟合直线所需要的角度精度,一般设置为0.01或1e-2。
实现思路

微卡智享
步骤
1
旋转矩形的点和上一步获取的最近点设置一个阈值距离,在距离内的都列入当前区域的直线拟合点,超过阈值的用最近点加上阈值重新算为计算点来进行拟合
2
根据不同区域计算直线拟合
3
求到的直线拟合点实现每两条求交点
4
得到的4个交点做为透视变换的坐标点
01
阈值范围内的直线拟合

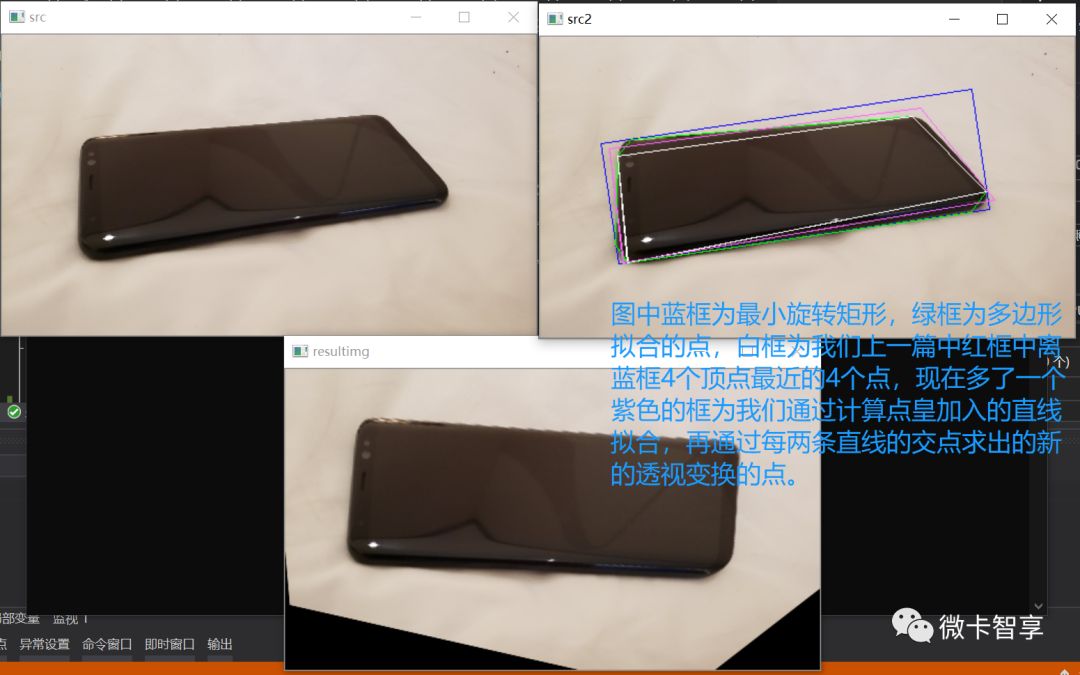
先以左边区域为例,首先我们设定了一个距离为15的阈值,白色的是我们上一篇中求到的最近的点(点1和2),蓝色为最小旋转矩形的角点(点3和4),我们通过计算点1到点3的距离,还有点2到点4的距离都小于15,那我们把这4个点都列入到左边区域,用来计算直接拟合。
 紫色线即为上面4个点采用直线拟合后的结果
紫色线即为上面4个点采用直线拟合后的结果
左边的区域拟合直线,因为都在阈值内,所以拟合出的直线比原来只求最近点连起来的效果要更好一点。接下来我们看看超过阈值的处理。
02
超出阈值的直线拟合

上图中可以看到,右下的区域点在阈值范围内是无问题了,右上的旋转矩形角点(点4)与最近点(点2)距离挺远,肯定超出阈值了,如果还把点4也加入到拟合点计算的话,直线会多出来不少,所以我们就在根据(点2)的坐标,在X轴和Y轴都加上阈值的范围,计算出新的拟合点,即上图红圈标识的,用点1,点2,点3和红色拟合点来进行直线拟合,得到的效果如下:

03
每两条直线拟合求交点

直线拟合的函数,输出的参数line里面有说到了是Vec4f的类型,输出参数的前半部分给出的是直线的方向,而后半部分给出的是直线上的一点(即通常所说的点斜式直线)。
方程式:y-y1=k(x-x1)
其中(x1,y1)为坐标系上过直线的一点的坐标,k为该直线的斜率。
推导:若直线L1经过点P1(x1,y1),且斜率为k,求L1方程。
设点P(x,y)是直线上不同于点P1的任意一点,直线PP1的斜率应等于直线L1的斜率,根据经过两点的直线的斜率公式得k=(y-y1)/(x-x1) (且:x≠x1)
所以,直线L1:y-y1=k(x-x1)
说明:
(1)这个方程是由直线上一点和斜率确定的,这一点必须在直线上,否则点斜式方程不成立;
(2)当直线l的倾斜角为0°时,直线方程为y=y1;
(3)当直线倾斜角为90°时,直线没有斜率,它的方程不能用点斜式表示,这时直线方程为x=x1。
我们直线拟合的得到的4个Vec4f就需要每两个求交点最后得到上图中红圈的1,2,3,4的4个交点。根据斜率和点的计算
kk1*x+b1=kk2*x+b2
可以得到:x=(b2-b1)/(kk1-kk2)
进而得到:y=(kk1*(b2-b1)/(kk1-kk2))+b1
核心代码

微卡智享
重新计算区域及直线拟合的函数
定义的默认阈值是15。
//采用重新定义点做直线拟合后找到的对应点
根据两点及斜率求交点
//求两条直线的交叉点
透视变换的新坐标代码
上一篇中透视变换的新坐标我们直接是用的最小外接矩形的4个点,不过个别图中会矩形特别大,整个透视变换后的拉伸有点太夸张了,所以这里我们改了方法,先求出最小旋转矩形中最左和最上的坐标,然后计算出最小旋转矩形的长和高,来定义一个新的矩形进行透视变换。
//根据最小矩形和多边形拟合的最大四个点计算透视变换矩阵
完

扫描二维码
获取更多精彩
微卡智享

「 往期文章 」
.Net5 Windows Form App中Linq的分组查询使用
本文分享自微信公众号 - 微卡智享(VaccaeShare)。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。