一、内积

1.1、定义

内积（inner product）又称数量积（ scalar product）、点积（dot product），是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。

两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为：
a·b=a1_b1+a2_b2+……+an*bn。

使用矩阵乘法并把（纵列）向量当作n×1 矩阵，点积还可以写为：

以上定义方法为代数定义，表示向量a和b的点积等于a的转置矩阵和矩阵b的乘积。向量是将几何问题转化为代数问题的桥梁，向量点积的计算其实也可以使用几何方式计算。

设二维空间内有两个向量a 和b ，它们的夹角为 θ（区间为[0,π]），则内积定义为以下实数：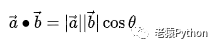

特别地，如果向量a和自己自乘，此时θ为0，cosθ=1，右边就变成了向量a的模的平方，左边变成了向量a的转置矩阵和a自身的乘积，所以才有上节的单位向量等式：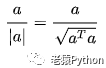

相关符号表示请参考《https://blog.csdn.net/LaoYuanPython/article/details/112410587 人工智能数学基础-线性代数1：向量的定义及向量加减法》的介绍。

注意：该定义只对二维和三维空间有效。

1.2、运算律

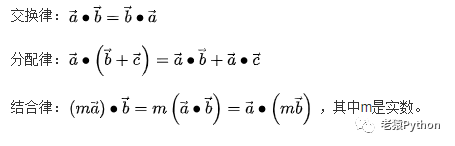
更多内容请参考百度文库关于点积的介绍

二、外积

2.1、外积定义

外积(outer product)又称为矢量积、叉积、矢积、叉乘、向量积，向量a和向量b的外积形成一个垂直于原来的向量a、b的向量c，c的长度等于a、b构成的平行四边形的面积。两个向量a、b的外积表示为：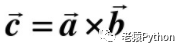

向量a、b外积的模与向量a的模和向量b的模的关系如下：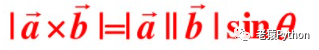

其中θ为向量a和向量b的夹角。

2.2、右手定则及外积方向

在三维坐标系中x、y、z为三个坐标轴，右手定则为伸开右手手掌，四个手指从x轴正方向方向转到y轴正方面，则大拇指方向即为z正轴方向。

向量a、b的外积向量c垂直于向量a和向量b，方向符合右手定则。

2.3、外积的代数表示

假设三维坐标系中，向量a（x1,y1,z1）、向量b(x2,y2,z2)的外积坐标可以通过如下方式计算得出：

`a × b = (x1,y1,z1)×(x2,y2,z2)=(y1*z2-y2*z1,z1*x2-z2*x1,x1*y2-x2*y1)  
`

*   1

2.4、外积相关公式

由于输入的问题，下面公式中的英文字母如非特别说明表示向量：

• 反对称性：a × b= - b× a

• 分配律：a × (b+c) = a ×b +a ×c

• 二重（双重）外积公式：a × (b×c )= b(a · c) − c(a ·b) 或 a×(b×c)=-(b×c)×a=(a·c)b-(a·b)c

• a × a= 0

• （ka）× b = a × (kb) = k(a × b )，其中k为实数，a、b为向量

更多外积参考资料请参考百度百科关于外积的解释。

三、小结

本文介绍了向量的內积和外积的概念，以及相关的运算公式。

写博不易，敬请支持：

如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！

更多人工智能数学基础的介绍请参考专栏《人工智能数学基础 》

本文转转自微信公众号老猿Python原创https://mp.weixin.qq.com/s/vt0fyAfQBVgPmjwyurjH8g，如有侵权，请联系删除。