应用场景：

应用于语音识别
语音翻译
机器翻译

RNN

RNN（Recurrent Neural Networks,循环神经网络）不仅会学习当前时刻的信息，也会依赖之前的序列信息。
由于其特殊的网络模型结构解决了信息保存的问题。所以RNN对处理时间序列和语言文本序列问题有独特的优势。递归神经网络都具有一连串重复神经网络模块的形式。在标准的RNNs中，这种重复模块有一种非常简单的结构。

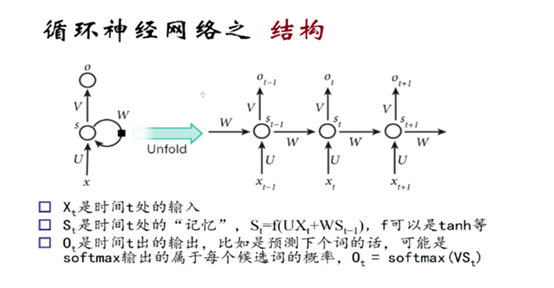
tensorflow 之循环神经网络

那么S(t+1) = tanh( U_X(t+1) + W_S(t))。tanh激活函数图像如下：

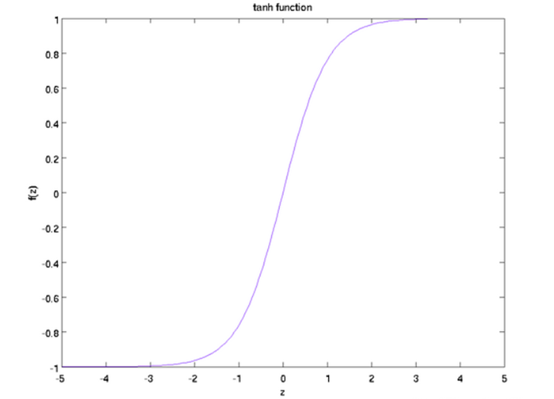
tensorflow 之循环神经网络

激活函数tanh把状态S值映射到-1和1之间.

RNN通过BPTT算法反向传播误差，它与BP相似，只不过与时间有关。RNN同样通过随机梯度下降(Stochastic gradient descent)算法使得代价函数(损失函数)值达到最小。

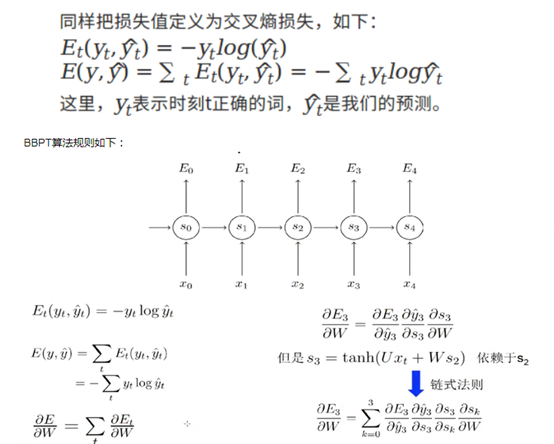
tensorflow 之循环神经网络

但是随着时间间隔不断增大时，RNN会丧失学习到连接很远的信息能力(梯度消失)。原因如下：

RNN的激活函数tanh可以将所有值映射到-1至1之间，以及在利用梯度下降算法调优时利用链式法则，那么会造成很多个小于1的项连乘就很快的逼近零。

依赖于我们的激活函数和网络参数，也可能会产生梯度爆炸（如激活函数是Relu，而LSTM采用的激活函数是sigmoid和tanh，从而避免了梯度爆炸的情况）。
一般靠裁剪后的优化算法即可解决，比如gradient clipping（如果梯度的范数大于某个给定值，将梯度同比收缩）。

合适的初始化矩阵W可以减小梯度消失效应，正则化也能起作用。更好的方法是选择ReLU而不是sigmoid和tanh作为激活函数。ReLU的导数是常数值0或1，所以不可能会引起梯度消失。更通用的方案时采用长短时记忆（LSTM）或门限递归单元（GRU）结构。

LSTM

LSTM (Long Short Term Memory networks)的“门”结构可以截取“不该截取的信息”，结构如下：

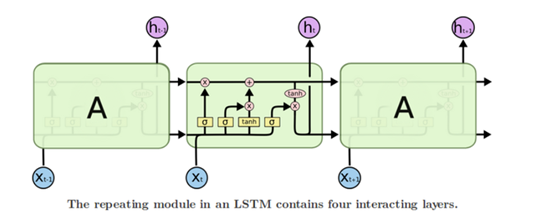
tensorflow 之循环神经网络

在上面的图中，每条线表示一个完整向量，从一个节点的输出到其他节点的输入。粉红色圆圈代表逐点操作，比如向量加法，而黄色框框表示的是已学习的神经网络层。线条合并表示串联，线条分叉表示内容复制并输入到不同地方。

LSTMs核心理念：

LSTMs的关键点是细胞状态，就是穿过图中的水平线。

单元状态有点像是个传送带。它贯穿整个链条，只有一些线性相互作用。这很容易让信息以不变的方式向下流动。

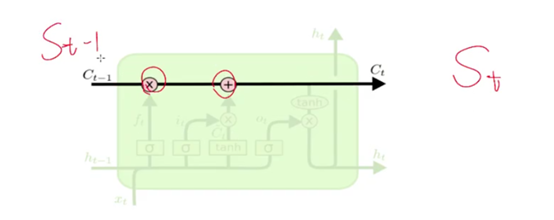
tensorflow 之循环神经网络

其中，C(t-1)相当于上面我们讲的RNN中的S（t-1）, C(t)相当于S(t).

LSTM有能力向单元状态中移除或添加信息，通过门结构来管理，包括“遗忘门”，“输出门”，“输入门”。通过门让信息选择性通过，来去除或增加信息到细胞状态. 模块中sigmoid层输出0到1之间的数字，描述了每个成分应该通过门限的程度。0表示“不让任何成分通过”，而1表示“让所有成分通过！”

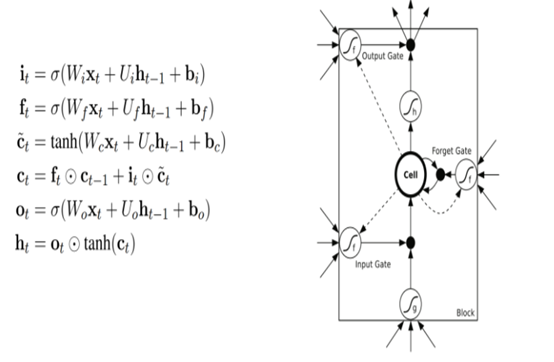
tensorflow 之循环神经网络

LSTM循环神经网络分步说明:

第一步: 确定过去什么信息可以通过 cell state

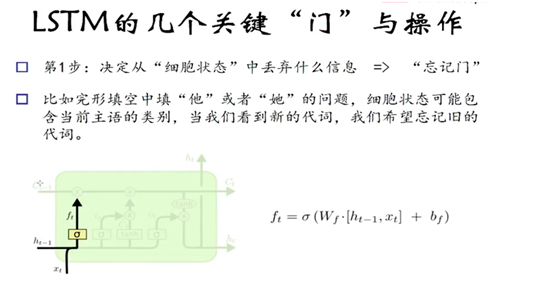
tensorflow 之循环神经网络

这个决定由忘记门通过sigmoid 来控制，他会根据上一时刻的输出h（t-1）和当前输入x(t)来产生一个[0,1]区间的f(t)值，来决定是否让上一时刻的信息c(t-1)通过或部分通过。

第二步：产生新信息

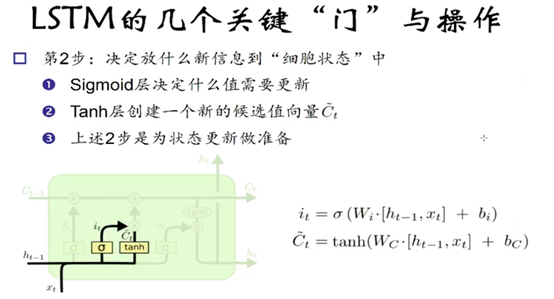
tensorflow 之循环神经网络

上图是输入门结构，i(t)等式表达的是我们以多大概率来更新信息，

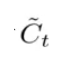
tensorflow 之循环神经网络

表示现在的全部信息。

这一部分包含两个部分，第一个是输入门(input gate)通过sigmoid来决定哪些值用来更新，第二个是一个tanh层，用来生成新的候选值c(t),他作为当期层产生的候选值可能会添加到 cell state中。我们会把这两部分产生的值结合来进行更新。

第三步：更新老的cell state

tensorflow 之循环神经网络

首先把旧状态 Ct-1与f(t)相乘，来忘掉我们不需要的信息，然后将

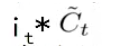
tensorflow 之循环神经网络

相加以确定要更新的信息，通过相加操作得到新的细胞状态Ct.。即丢掉不需要的信息，添加新信息的过程。

第四步：决定模型的输出

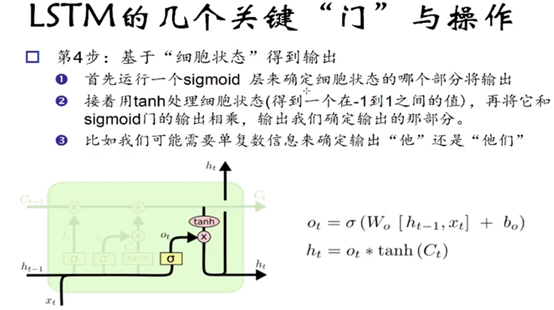
tensorflow 之循环神经网络

首先通过运行一个 sigmoid层决定cell状态输出哪一部分。随后我们cell状态通过tanh函数，将Ct输出值保持在 -1到1之间。之后我们再乘以sigmoid门输出值，即得结果。

至此，我们在这里再次强调一下LSTM是如何解决长时依赖问题的: 在RNN中，当前状态值S（t）= tanh(x(t) * U + W * S(t-1))，正如上面所述在利用梯度下降算法链式求导时是连乘的形式，若其中只要有一个是接近零的，那么总体值就容易为0，导致梯度消失，不能解决长时依赖问题。而LSTM更新状态值：

是相加的形式，所以不容易出现状态值逐渐接近0的情况。

Sigmoid函数的输出是不考虑先前时刻学到的信息的输出，tanh函数是对先前学到的信息的压缩处理，起到稳定数值的作用，两者的结合就是循环神经网络的学习思想。

代码演示

"""
demo 使用单层 LSTM网络 对 MNIST数据集分类

循环神经网络-具有记忆功能的网络
前面的内容可以理解为 静态数据的处理，即样本是单次的，彼此之间没有关系。
而人工智能对计算机的要求不仅仅是单次的运算，还需要让计算年纪像人一样具有记忆功能。
循环神经网络RNN，是一个具有记忆功能的网络，最适合解决连续序列问题。

RNN网络应用领域：
对于序列化的特征任务，都适合采用RNN网络来解决。情感分析，关键词提取，语音识别，机器翻译，股票分析。
lstm 长短期记忆网络
gru 闸门重复单元
"""

import tensorflow as tf
import numpy as np
# 导入 MINST 数据集
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True) # 在线下载 MNIST_data 数据集

n_input = 28 # MNIST data 输入 (img shape: 28*28)
n_steps = 28 # 序列个数
n_hidden = 128 # hidden layer num of features
n_classes = 10  # MNIST 列别 (0-9 ，一共10类)

tf.reset_default_graph()

# tf Graph input
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes])


x1 = tf.unstack(x, n_steps, 1)


#1 BasicLSTMCell  0.9453125
lstm_cell = tf.contrib.rnn.BasicLSTMCell(n_hidden, forget_bias=1.0)
outputs, states = tf.contrib.rnn.static_rnn(lstm_cell, x1, dtype=tf.float32)

#2 LSTMCell  0.9609375
# lstm_cell = tf.contrib.rnn.LSTMCell(n_hidden, forget_bias=1.0)
# outputs, states = tf.contrib.rnn.static_rnn(lstm_cell, x1, dtype=tf.float32)

#3 gru 0.9921875
# gru = tf.contrib.rnn.GRUCell(n_hidden)
# outputs = tf.contrib.rnn.static_rnn(gru, x1, dtype=tf.float32)

#4 创建动态RNN 0.9921875
# outputs,_  = tf.nn.dynamic_rnn(gru,x,dtype=tf.float32)
# outputs = tf.transpose(outputs, [1, 0, 2])

pred = tf.contrib.layers.fully_connected(outputs[-1],n_classes,activation_fn = None)



learning_rate = 0.001
training_iters = 100000
batch_size = 128
display_step = 10

# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)

# Evaluate model
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

# 启动session
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    step = 1
    # Keep training until reach max iterations
    while step * batch_size < training_iters:
        batch_x, batch_y = mnist.train.next_batch(batch_size)
        # Reshape data to get 28 seq of 28 elements
        batch_x = batch_x.reshape((batch_size, n_steps, n_input))
        # Run optimization op (backprop)
        sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
        if step % display_step == 0:
            # 计算批次数据的准确率
            acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
            # Calculate batch loss
            loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y})
            print ("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
                   "{:.6f}".format(loss) + ", Training Accuracy= " + \
                   "{:.5f}".format(acc))
        step += 1
    print (" Finished!")

    # 计算准确率 for 128 mnist test images
    test_len = 128
    test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_input))
    test_label = mnist.test.labels[:test_len]
    print ("Testing Accuracy:", \
           sess.run(accuracy, feed_dict={x: test_data, y: test_label}))

运行结果：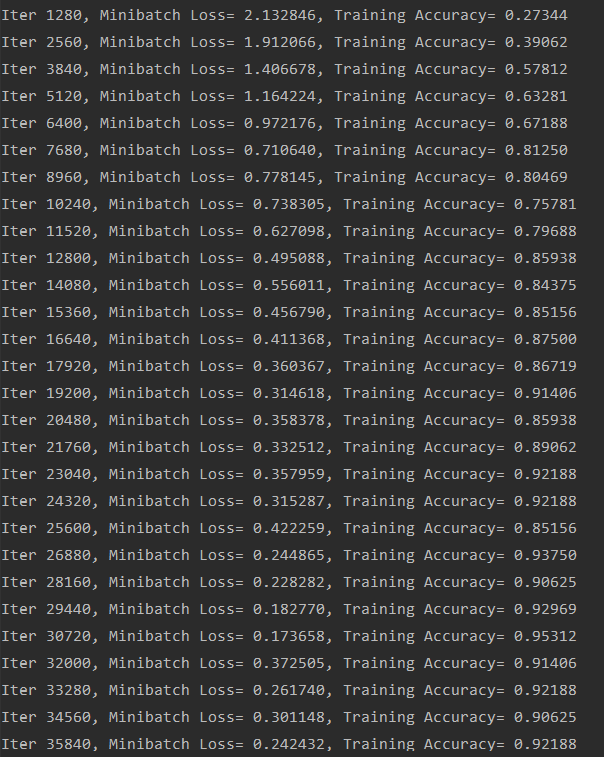
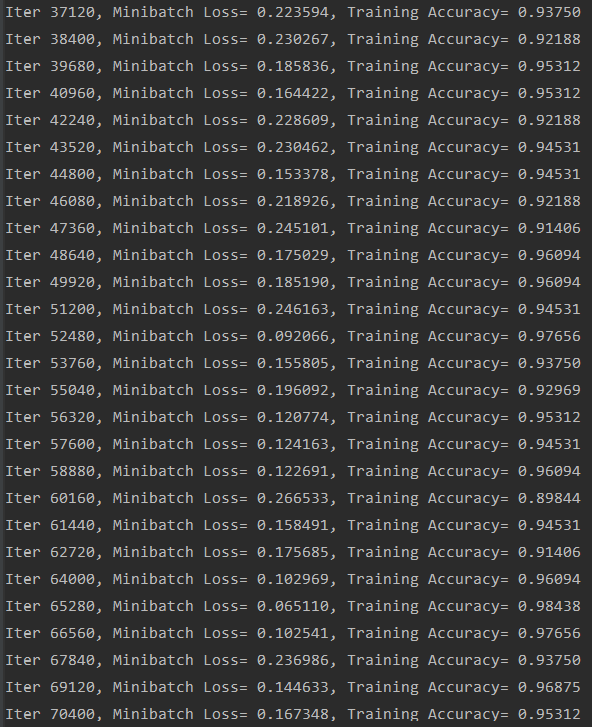
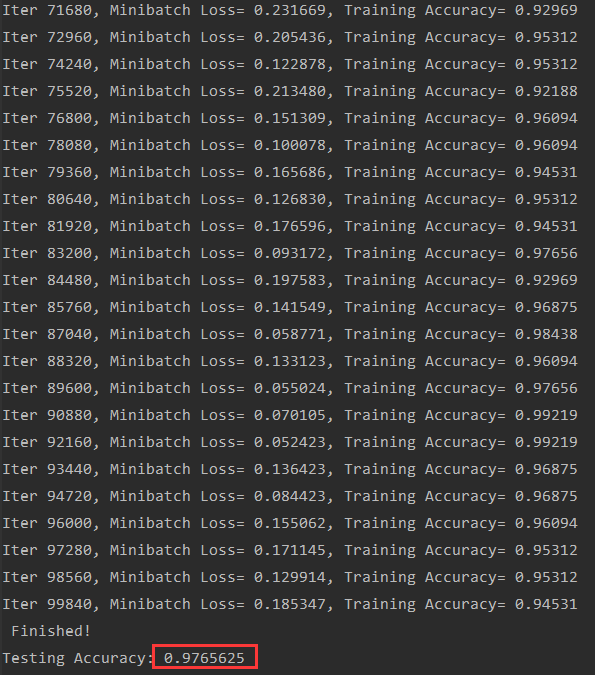
tensorflow 之循环神经网络