1、典型问题

问题一：条件判断超预期

System.out.println(1f == 0.9999999f)    // false
System.out.println(1f == 0.99999999f)   // true

问题二：数据转换超预期

float f = 1.1f;
double d = (double)f;
System.out.println(f);  // 1.1
System.out.println(d);  // 1.100000023841858

问题三：基本运算超预期

System.out.println( 0.2 + 0.7 ); // 0.8999999999999999 

问题四：数据自增超预期

float f1 = 8455263f;  // 7位数
for (int i = 0; i < 10; i++) {
    System.out.println(f1);
    f1++;
}
// 打印：8455263.0
// 打印：8455264.0
// 打印：8455265.0
// 打印：8455266.0
// 打印：8455267.0
// 打印：8455268.0
// 打印：8455269.0
// 打印：8455270.0
// 打印：8455271.0
// 打印：8455272.0

float f2 = 84552631f;  // 8位数
for (int i = 0; i < 10; i++) {
    System.out.println(f2);
    f2++;
}
//    打印：8.4552632E7
//    打印：8.4552632E7
//    打印：8.4552632E7  
//    打印：8.4552632E7 
//    打印：8.4552632E7
//    打印：8.4552632E7
//    打印：8.4552632E7
//    打印：8.4552632E7
//    打印：8.4552632E7
//    打印：8.4552632E7

2、浮点数的精度问题

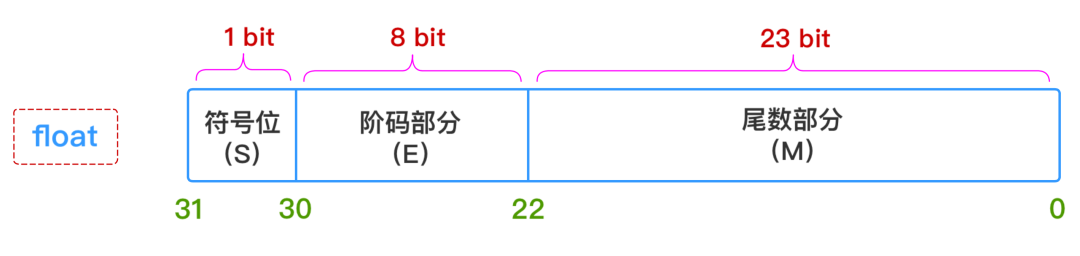
浮点数在计算机中的存储方式遵循IEEE 754 浮点数计数标准，可以用科学计数法表示为： 对于float和double两种浮点数在内存中的存储结构如下图所示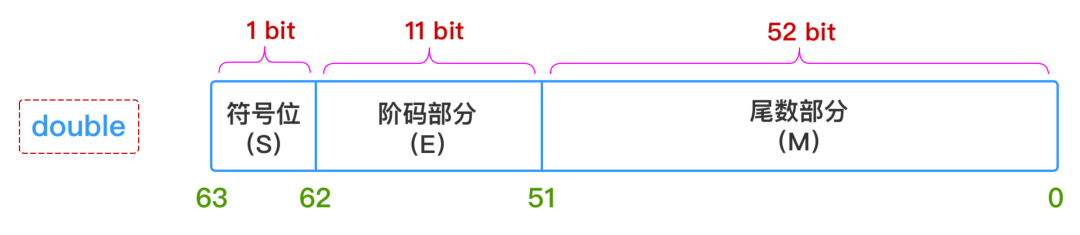： 1、符号部分（S）

• 0-正
• 1-负

2、阶码部分（E）(指数部分)

• 对于float型浮点数，指数部分8位，考虑可正可负，因此可以表示的指数范围为-127 ~ 128
• 对于double型浮点数，指数部分11位，考虑可正可负，因此可以表示的指数范围为-1023 ~ 1024

3、尾数部分（M） 浮点数的精度是由尾数的位数来决定的：

• 对于float型浮点数，尾数部分23位，换算成十进制就是 2^23=8388608，所以十进制精度只有6 ~ 7位；
• 对于double型浮点数，尾数部分52位，换算成十进制就是 2^52 = 4503599627370496，所以十进制精度只有15 ~ 16位

所以，上述0.99999999f超出float型浮点数据的精度范围。

3、如何解决精度问题

• 用字符串或者数组解决多位数问题
• Java的大数类：BigDecimal、BigInteger

  BigDecimal num3 = new BigDecimal( Double.toString( 1.0f ) );
  BigDecimal num4 = new BigDecimal( Double.toString( 0.99999999f ) );
  System.out.println( num3 == num4 );  // 打印 false
  

BigDecimal num1 = new BigDecimal( Double.toString( 0.2 ) ); BigDecimal num2 = new BigDecimal( Double.toString( 0.7 ) );

// 加 System.out.println( num1.add( num2 ) ); // 打印：0.9

// 减 System.out.println( num2.subtract( num1 ) ); // 打印：0.5

// 乘 System.out.println( num1.multiply( num2 ) ); // 打印：0.14

// 除 System.out.println( num2.divide( num1 ) ); // 打印：3.5

局限性：大数类的运算效率肯定是不如原生类型效率高，代价还是比较昂贵的，是否选用需要根据实际场景来评估。