人工智能数学基础-线性代数3：线性空间、线性相关及基

一、向量空间（线性空间）及基域

线性空间是在考察了大量的数学对象(如几何学与物理学中的向量，代数学中的n元向量、矩阵、多项式，分析学中的函数等)的本质属性后抽象出来的数学概念。

1.1、详细定义

向量空间也称线性空间，设V是一个非空集合，P是一个数域。若：

在V中定义了一种运算，称为加法，即对V中任意两个元素α与β都按某一法则对应于V内惟一确定的一个元素α+β，称为α与β的和;
在P与V的元素间定义了一种运算，称为纯量乘法(亦称数量乘法)，即对V中任意元素α和P中任意元素k，都按某一法则对应V内惟一确定的一个元素kα，称为k与α的积;
加法与纯量乘法满足以下条件：
1)、α+β=β+α，对任意α，β∈V.
2)、α+(β+γ)=(α+β)+γ，对任意α，β，γ∈V.
3)、存在一个元素0∈V，对一切α∈V有α+0=α，元素0称为V的零元.
4)、对任一α∈V，都存在β∈V使α+β=0，β称为α的负元素，记为-α.
5)、对P中单位元1，有1α=α(α∈V).
6)、对任意k，l∈P，α∈V有(kl)α=k(lα)
7)、对任意k，l∈P，α∈V有(k+l)α=kα+lα.
8)、对任意k∈P，α，β∈V有k(α+β)=kα+kβ
则称V为域P上的一个线性空间，或向量空间。V中元素称为向量，V的零元称为零向量，P称为线性空间的基域。当P是实数域时，V称为实线性空间；当P是复数域时，V称为复线性空间。

1.2、公理化定义

设F是一个域。一个F上的向量空间是一个集合V的两个运算：

向量加法: V + V → V, 记作 v + w，v、w∈V
标量乘法: F × V → V, 记作 a·v， a∈F, v∈V
符合下列公理 (∀ a, b ∈ F 及 u, v, w ∈ V)：

向量加法结合律：u + (v + w) = (u + v) + w；
向量加法交换律：v + w = w + v；
向量加法的单位元：V里有一个叫做零向量的 0，∀ v ∈ V , v + 0 = v；
向量加法的逆元素：∀v∈V, ∃w∈V，使得 v + w = 0；
标量乘法分配于向量加法上：a(v + w) = a v + a w；
标量乘法分配于域加法上: (a + b)v = a v + bv；
标量乘法一致于标量的域乘法: a(b v) = (ab)v；
标量乘法有单位元: 1 v = v, 这里 1 是指域 F的乘法单位元。
V 闭合在向量加法下：v + w ∈ V
V 闭合在标量乘法下：a v ∈ V

有些教科书还强调以下两个公理：
V 闭合在向量加法下：v + w ∈ V
V 闭合在标量乘法下：a v ∈ V

V的成员叫作向量，而F的成员叫作标量。若F是实数域R，V称为实向量空间；若F是复数域C，V称为复向量空间；若F是有限域，V称为有限域向量空间；对一般域F，V称为F-向量空间。

向量空间举例

若V为数域P上全体m×n矩阵组成的集合Mmn§，V的加法与纯量乘法分别为矩阵的加法和数与矩阵的乘法，则Mmn§是数域P上的线性空间，V中向量就是m×n矩阵；
域P上所有n元向量(a1，a2，…，an)构成的集合P对于加法：(a1，a2，…，an)+(b1，b2，…，bn)=(a1+b1，a2+b2，…，an+bn)与纯量乘法：λ(a1，a2，…，an)=(λa1，λa2，…，λan)构成域P上的线性空间，称为域P上n元向量空间。

二、线性相关和线性无关

2.1、线性表示

假定a1、a2、…、as是s个n维向量，k1,…，ks是s个数，那么：
k1a1+k2a2+…+ksas
称其为a1、a2、…、as的线性组合，如果：
a = k1a1+k2a2+…+ksas
那么a也是a1、a2、…、as的线性组合，或者叫a1、a2、…、as的线性表示。

2.2、线性相关、线性无关

在一个线性空间中，如果一组向量a1、a2、…、as（其中s>=1）从：
k1*a1+k2*a2+......+ks*as = 0
可以推出k1=k2=…=ks=0，则称这组向量线性无关。

反之，如果在一个线性空间中，如果存在一组不全为0的k1、k2、…、ks（s>=1），一组向量a1、a2、…、as有如下等式成立：
k1*a1+k2*a2+......+ks*as = 0
则称这组向量线性相关。

https://www.zhihu.com/question/21605094

2.3、线性子空间

设W为向量空间 V 的一个非空子集，若W在 V 的加法及标量乘法下是封闭的，且零向量0 ∈ W，就称W为 V 的线性子空间
给出一个向量集合 B，那么包含它的最小子空间就称为它的扩张，记作 span(B)。另外可以规定空集的扩张为{0}
给出一个向量集合 B，若它的扩张就是向量空间 V，则称 B 为 V 的生成集合
给出一个向量集合 B，若B是线性无关的，且B能够生成V，就称B为V的一个基。若 V={0}，唯一的基是空集。对非零向量空间 V，基是 V 最小的生成集

三、极大线性无关组

3.1、简介

极大线性无关组（maximal linearly independent system）是在线性空间中拥有向量个数最多的线性无关向量组。

设V是域P上的线性空间，S是V的子集。若S的一部分向量线性无关，但在这部分向量中，加上S的任一向量后都线性相关，则称这部分向量是S的一个极大线性无关组。

V中子集的极大线性无关组不是唯一的，例如，V的基都是V的极大线性无关组。它们所含的向量个数（基数）相同。V的子集S的极大线性无关组所含向量的个数（基数），称为S的秩。只含零向量的子集的秩是零。

V的任一子集都与它的极大线性无关组等价。特别地，当S等于V且V是有限维线性空间时，S的秩就是V的维数。

3.2、定义

设有向量组 A：a1、a2、…、as ，若 A中能选出r个向量，满足:
(1)向量组 A0：a1、a2、…、ar 线性无关；
(2) 向量组A 中任意r+1个向量（若有的话）都线性相关，则称向量组A0是向量组A的一个极大线性无关组（简称为极大无关组）。

线性方程组系数矩阵的极大线性无关组称为该线性方程组的基础解系。

四、线性空间的基

前面2.2部分简单介绍了基的概念，由于基的重要性，本部分对基进行一个详细的介绍。

4.1、简介

在线性代数中，基(basis)（也称为基底），线性空间的基（basis of a linear space）是描述、刻画向量空间的基本工具。

向量空间的基是它的一个特殊的子集，基的元素称为基向量。向量空间中任意一个元素，都可以唯一地表示成基向量的线性组合。如果基中元素个数有限，就称向量空间为有限维向量空间，将基中元素的个数称作向量空间的维数。

不是所有空间都拥有由有限个元素构成的基底。这样的空间称为无限维空间。某些无限维空间上可以定义由无限个元素构成的基。

任何向量空间都拥有一组基。一个向量空间的基不止一组，但同一个空间的两组不同的基，它们的元素个数或势（当元素个数是无限的时候）是相等的。

一组基里面的任意一部分向量都是线性无关的；反之，如果向量空间拥有一组基，那么在向量空间中取一组线性无关的向量，一定能将它扩充为一组基。

4.2、定义

给定一个向量空间V ，V的一组基B是指V里面的可线性生成V的一个线性无关子集。B的元素称为基向量。

更详细来说，设B={e1,e2,…,en}是在系数域F（比如实数域R或复数域C）上的向量空间V的有限子集。如果满足下列条件：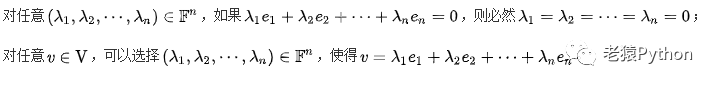
人工智能数学基础-线性代数3：线性空间、线性相关及基
就说B 是向量空间V 的一组基。第二个条件中，将一个向量v∈V表示成λ1*e1+λ2*e2+...+λn*en的形式，称为向量 v在基底下的分解。(λ1,λ2,…,λn)称为向量v在基底B下的分量表示。

只存在有限基的向量空间叫做有限维的空间。要处理无限维的空间，必须把上述基的定义推广为包括无限的基集合。如果向量空间V的一个子集 (有限或无限)B满足：
它的所有有限子集B’⊂B，满足上面的第一个条件（即线性无关）；
对任意v∈V，可以选择(λ1,λ2,…,λn)∈Fn，以及e1、e2、…、en∈B，使得:
v = λ1*e1+λ2*e2+...+λn*en。就称B是无限维空间V的一组基。

4.3、解释

设B是向量空间V的子集，则B是基，当且仅当满足了下列任一条件：

V是B的极小生成集，就是说只有B能生成V ，而它的任何真子集都不能生成全部的向量空间
B是V中线性无关向量的极大集合，就是说B在V中是线性无关集合，而且V中没有其他线性无关集合包含它作为真子集
V中所有的向量都可以按唯一的方式表达为B中向量的线性组合。如果基是有序的，则在这个线性组合中的系数提供了这个向量关于这个基的坐标

另外关于基和向量空间有如下规则：

一个向量空间的所有基都拥有同样的势（元素个数），叫做这个向量空间的维度，这个结果叫做维度定理
任何的向量空间都拥有一组基，任何一组基都对应一个向量空间
如果向量空间拥有一组基，那么每个线性无关的子集都可以扩张成一组基（也称为基的扩充定理），每个能够生成整个空间的子集也必然包含一组基。特别地，在任何线性无关集合和任何生成集合之间有一组基。以数学语言来说：如果L是在向量空间中的一个线性无关集合而集合G是一个包含L而且能够生成V的集合，则存在V 的一组基B，它包含了L而且是G的子集：L⊆B⊆G
n维线性空间中，任意n个线性无关的向量构成的向量组，都是空间的基。
相关证明需要使用更多的知识，老猿没有进一步研究，大家记得即可。

4.4、例子

考虑所有坐标 (a,b)的向量空间R，这里的a和b都是实数。则非常自然和简单的基就是向量e1= (1,0)和e2= (0,1):假设v= (a,b)是R中的向量，则v=a(1,0) +b(0,1)。而任何两个线性无关向量如 (1,1)和(−1,2)，也形成R的一个基。
给定自然数n和n个线性无关的向量e1,e2, …,en，e1,e2, …,en可以在实数域上生成R。因此，它们也是一个基而R的维度是n，这个基叫做R的标准基

4.5、有序基和坐标

基是作为向量空间的子集定义的，其中的元素并不按照顺序排列。为了更方便相关的讨论，通常会将基向量进行排列。例如将：B={e1,e2,…,en} 写成有序向量组：（e1,e2,…,en）。这样的有序向量组称为有序基。在有限维向量空间和可数维数的向量空间中，都可以自然地将基底表示成有序基。在有序基下，任意的向量都可以用确定的数组表示，该数组称为向量的坐标。例如，在使用向量的坐标表示的时候习惯谈论“第一个”或“第二个”坐标，这只在指定了基的次序前提下有意义。在这个意义下，有序基可以看作是向量空间的坐标架。

定义：在线性空间Vn(F)中，设{α1，α2，…，αn}是一组基，β为V中的一个元素，{α1，α2，…，αn，β}线性相关，故β可由α1，α2，…，αn唯一线性表示，因此有：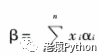
人工智能数学基础-线性代数3：线性空间、线性相关及基
则称数x1,x2,…,xn是β在基{α1，α2，…，αn}下的坐标。