GitHub仓库地址:https://github.com/djybbb/Intelligent-Scissors
边缘特征
我们观察到,磁力套索会自动地去贴合图像中物体的边缘,而图像的边缘特征可以由图像像素的一阶导数和二阶导数描述,故图像中梯度幅值和拉普拉斯算子响应值较高的更可能是图像中的边缘。
算法思路
设置初始点
整个程序的操作流程是这样的,用户首先在想要的轮廓附近设置一个初始点(称之为seed point),然后移动鼠标,在这个过程中曲线会自动地去贴合图像物体的轮廓。
最小代价路径
而该过程可以建模成Dijkstra算法,即设置seed point后,程序计算出图像中所有的像素点到seed point的最小代价路径。
回想到前面所说的边缘特征,此处的代价与边缘特征有关,即边缘特征越明显的像素点,其代价越低,这样便使得最小代价路径总是会去“贴合”图像的边缘。
像素节点类
从前面可以看到,每个像素会被标记,记录其要到seed point的话,下一步该走到哪一个像素,故其类应该要包含指向另一个像素节点的指针。
同时,每个节点都要知道自己到seed point的总代价(该值的存在是为了不断地做对比来得到最短路径)。
故像素节点类最基本的元素如下:
class GraphNode {
public:
int x;
int y;
double global_cost;//到seed point的总代价
GraphNode * back_pointer;//最小代价路径的方向
...//
};
Active List类
回忆Dijkstra算法,我们需要不停地知道当前最小代价的路径是哪一处,以决定我们下一次循环将要处理哪个节点类。于是我们使用Active List类来存储当前待遍历的像素点,并且Active List能够直接访问到当前代价最低的像素点。
论文中用了较为复杂的桶排序,其效率很高。我的实现中使用了一个一直维持有序的List,可以参考代码中的ActiveList.cpp。这里就不介绍了。。。(效率不高的实现,但是省事)
代价Local Costs描述
我们称之前提到的代价为local costs,论文一中,Local Costs由三个图像特征组成
local costs通过这三个Image Feature的权重合得到: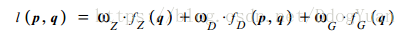
其中最为重要的是fG,即图像的梯度幅值。
fG的实现
设图像像素坐标为(x,y)处的梯度幅值为M(x,y),有: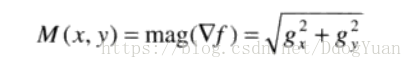
使用sobleFilter,其最小的3X3模版使用以z5为中心的一个3X3领域对gx和gy的近似如下式所示: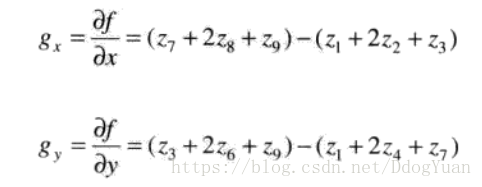
梯度幅值越大,意味着具有更多的边缘特征,在前面的建模中提到边缘特征意味着路径代价低,故f(G)应该这样设置: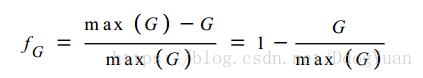
实现了fG之后就可以看到明显的效果,建议先实现f(G)再慢慢补充fZ和fD。fZ和fD的具体实现可以参考论文,其作用分别是使得曲线更加贴合边缘和更加平滑。
fZ的实现
意义
fZ是拉普拉斯零交(Laplacian Zero-Crossing)带来的代价,拉普拉斯算子的卷积就是原图像素二维导数,表示的图像一维导数变化的速率。拉普拉斯算子卷积为0的地方意味着该点是一维导数变化的极值点,其变化速率最快,我们认为这是边缘的特征,故其代价应该较低。我们将拉普拉斯算子卷积为0的地方的代价设为0,不为0的地方设为1。
特殊处理
由于拉普拉斯算子卷积刚好为0的地方极少,所以我们需要特殊处理以增多代价为0的点。
我们认为,当两个临近像素出现异号时,其中间肯定有卷积为0的位置,但是由于像素是离散的,我们设卷积值离0近的像素的代价为0,这样就增多了代价为0的点,使得拉普拉斯零交特征的影响增大。
fD的实现
意义
fD是为了使得边缘平滑,实现平滑的方式是通过为剧烈变化的边界方向设置较高的代价。
实现方法
设D(p)为某个像素点的梯度方向(Ix,Iy),其中Ix和Iy分别为图像在x方向和y方向上的梯度,D’(p)为(Iy,-Ix),与D(p)正交。设L(p,q)为p到q的单位向量。fD的详尽计算公式参考论文。
示例如下

算法流程描述
下图(a)描述了各个像素点的local costs,(a)中画圈的local cost为2的像素点代表着seed point,设其为S
设置seed point后,计算图像所有像素到该点的代价,其过程如(b) (c) (d)所示: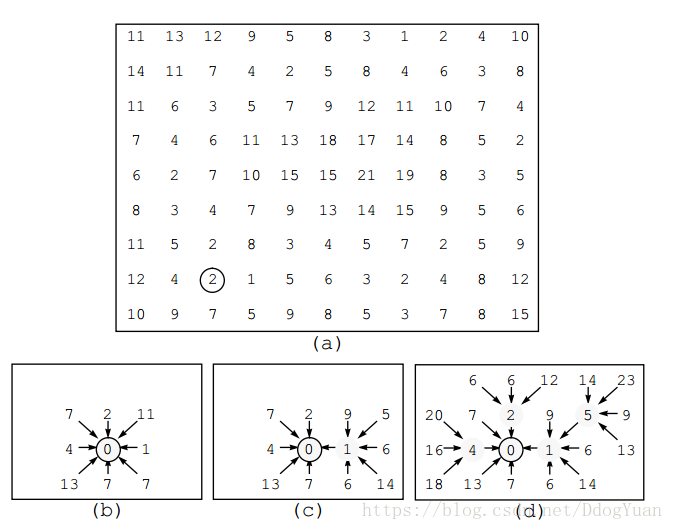
(b)
第一步,计算S的邻域(8个像素点)到S的代价,注意对照(a),S本身的local cost为2没有任何作用,因为S到自身的代价为0(这不是废话嘛。。。),邻域到S的代价不是local costs相减(例如S的左边像素自身的local costs为4,它到S的代价不是4-2,而是4),还有就是对角线上的像素到S的代价是其自身的local cost乘上了根号2,这是因为对角线的长度比直线长度长。
(c)
第二步,选取当前代价最低的路径(回忆Dijkstra算法)(a)中此时的路径只有其邻域到S的路径,其右方邻域像素N1到S的代价最低,标记N1:它要到达seed point,就走它的左邻域,这样可以使得总代价最小。
其中,N1的代价指的是便是N1到seed point的代价和。
然后计算N1的邻域到N1的代价,N1的邻域的代价不仅仅是其local cost的值,还要加上N1自身的代价(这样才是总代价)。观察下(b)图中S的右上方邻域像素(其 local cost为11)N2,对照©,发现其箭头指向了N1,并且其代价值更新为了9,这是因为在第二步中,计算得到N2的代价为8+1 = 9,它比原来8*根号2 = 11要小,故需要进行更新。
更新意味着,N2此时知道自己要去到seed point的最小代价路径是走下方而不是左下方直接去seed point,这里也需要一个标记动作。(类似前面标记N1)
一次expand
以上两步可以称为一次expand
下一次expand也是类似,选取当前代价最低的路径,例如下一次expand应该选取的是S的上方像素(可以看到,是从全局来选取)。
伪代码参考
论文中把得到最小路径的算法称为:Live-Wire 2-D DP graph search
该伪代码的实现可参考项目代码中GraphSearch.cpp中的void calPath(CvPoint start_point)函数。
系列博客与总结
Intelligent Scissors 介绍 :https://blog.csdn.net/DdogYuan/article/details/80371070
Intelligent Scissors 绘图功能的构建:https://blog.csdn.net/DdogYuan/article/details/80371116
Intelligent Scissors 原理与实现:https://blog.csdn.net/DdogYuan/article/details/80554873
本文分享 CSDN - 阿元呐。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。










