一、数学符号
下列数学符号都是希腊字母,含义如下:
∀:“任意”
∃:“存在”
∈:“属于”
∉:“不属于”
א:阿列夫,用于表示集合的势(元素的个数)
δ、Δ:德尔塔,表示变化值
E、ε:伊普西龙,对数之基数,在概率统计中E用于表示级数和
ζ:截塔,方位角
η:艾塔 ,用作一般变量
Θ θ :西塔,一般表示角
∧ λ :兰布达,一般表示体积或变量
ξ:克西
Ω ω:欧米伽,一般表示角或变量
Ψ ψ:普西,一般表示角或变量
Φ φ:佛爱,一般表示角或变量
∑ σ:西格马,表示和,在概率统计中σ用于表示标准差
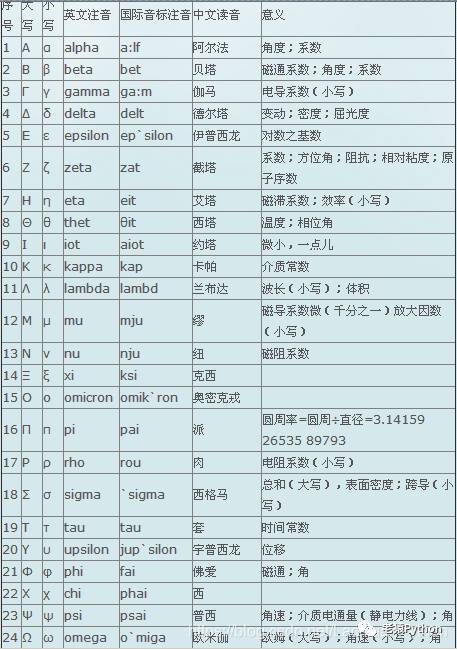
二、常用希腊字母及在数学和物理方面的含义
三、势
实数是稠密的和有序的,自然数、整数是离散的有序的,这些不同的数对应的集合的元素个数都是无穷的,但其元素个数可能相同也可能不同,集合元素的个数称为势。
势:集合元素的个数称为势;
等势:A和B两个集合的元素一个个能对应起来就是等势,例如自然数和整数是等势的,因为每个整数i(含负数)都能用一个自然数如2_abs(i)或2_abs(i)-1对应(abs表示绝对值),如:0对应0,-1对应1,1对应2,…。
自然数、整数、有理数等势,实数、实数的平方、复数等势,但后者的势大于前者的势,前者的势为ℵ₀(阿列夫0),后者为ℵ₁(阿列夫1);
注:阿列夫数,又称艾礼富数,在集合论这一数学分支里,阿列夫数是一连串超穷基数。其标记符号为 ℵ (由希伯来字母 א 演变而来)加角标表示可数集(包括自然数)的势标记为ℵ₀ ,下一个较大的势为ℵ₁ ,再下一个是ℵ2(如单元连续函数的个数),以此类推。一直继续下来,便可以对任一序数 α 定义一个基数。ℵ₀<ℵ₁<ℵ2…,对于学习AI来说,暂时知道ℵ₀、ℵ₁、ℵ2三个数就够了
本文转转自微信公众号老猿Python原创https://mp.weixin.qq.com/s/NGMg84AUJkUIlsd0mJOVdA,如有侵权,请联系删除。













