Python 图像处理（一）PIL - HelloWorld开发者社区

以前做图像处理时用的是matlab，但是matlab有一些不方便支出：

不开源，当时使用的版本是破解版的，至于版权问题，此处就不讨论了；
其一般只能用于实现，如果实现产业化则有很多不便；
程序运行比较慢；
与其他语言结合有点小问题。当进入工作岗位之后，做的是大数据方向，接触了java与python后感觉python对于做图像处理会更加好，所以此处简单的对python操作图像做一些简单的介绍。

首先安装pytyhon，linux系统中已经自己带了python，至于在window系统只安装则更加简单，下载一个Anaconda直接就可以安装了，后续的模块安装则直接使用pip安装会更加方便。在此处就不一一讲述了。

图像打开与显示

from PIL import Image
import numpy as np
import scipy
import matplotlib.pyplot as plt
lena = Image.open('lena.jpg')           //打开图像  
print(lena.mode)                       //打印图像类型
print(lena.getpixel((0,0)))           //打印图像(0,0)处像素值
lena.show()                            //图像显示

图像类型转化convert函数

python图像处理库PIL对于PNG、BMP和JPG彩色图像格式之间的互相转换都可以通过Image模块的open()和save()函数来完成。具体说就是，在打开这些图像时，PIL会将它们解码为三通道的“RGB”图像。用户可以基于这个“RGB”图像，对其进行处理。处理完毕，使用函数save()，可以将处理结果保存成PNG、BMP和JPG中任何格式。这样也就完成了几种格式之间的转换。同理，其他格式的彩色图像也可以通过这种方式完成转换。当然，对于不同格式的灰度图像，也可通过类似途径完成，只是PIL解码后是模式为“L”的图像。我们以图像 Python 图像处理（一）PIL 为例，分辨率为512x512。

模式“RGB”转换为其他不同模式

a. 模式“1” 模式“1”为二值图像，非黑即白。但是它每个像素用8个bit表示，0表示黑，255表示白。下面我们将lena图像转换为“1”图像。

lena_1 = lena.convert("1")
print(lena_1.mode)
lena_1.show()

b. 模式“L”
模式“L”为灰色图像，它的每个像素用8个bit表示，0表示黑，255表示白，其他数字表示不同的灰度。在PIL中，从模式“RGB”转换为“L”模式是按照下面的公式转换的： L = R * 299/1000 + G * 587/1000+ B * 114/1000 下面我们将lena图像转换为“L”图像。

lena_1 = lena.convert("L")
print(lena_1.mode)
lena_1.show()

c模式“P”
模式“P”为8位彩色图像，它的每个像素用8个bit表示，其对应的彩色值是按照调色板查询出来的。下面我们使用默认的调色板将lena图像转换为“P”图像。

lena_1 = lena.convert("P")
print(lena_1.mode)
lena_1.show()

d 模式“RGBA” 模式“RGBA”为32位彩色图像，它的每个像素用32个bit表示，其中24bit表示红色、绿色和蓝色三个通道，另外8bit表示alpha通道，即透明通道。

lena_1 = lena.convert("RGBA")
print(lena_1.mode)
lena_1.show()

e 模式“CMYK” 模式“CMYK”为32位彩色图像，它的每个像素用32个bit表示。模式“CMYK”就是印刷四分色模式，它是彩色印刷时采用的一种套色模式，利用色料的三原色混色原理，加上黑色油墨，共计四种颜色混合叠加，形成所谓“全彩印刷”。四种标准颜色是：C：Cyan = 青色，又称为‘天蓝色’或是‘湛蓝’M：Magenta = 品红色，又称为‘洋红色’；Y：Yellow = 黄色；K：Key Plate(blacK) = 定位套版色（黑色）。

从实例中可以得知PIL中“RGB”转换为“CMYK”的公式如下： C = 255 - R M = 255 - G Y = 255 - B K = 0 由于该转换公式比较简单，转换后的图像颜色有些失真。

f 模式“YCbCr” 模式“YCbCr”为24位彩色图像，它的每个像素用24个bit表示。YCbCr其中Y是指亮度分量，Cb指蓝色色度分量，而Cr指红色色度分量。人的肉眼对视频的Y分量更敏感，因此在通过对色度分量进行子采样来减少色度分量后，肉眼将察觉不到的图像质量的变化。模式“RGB”转换为“YCbCr”的公式如下： Y= 0.257_R+0.504_G+0.098_B+16 Cb = -0.148_R-0.291_G+0.439_B+128 Cr = 0.439_R-0.368_G-0.071*B+128

按照公式，Y = 0.257_197+0.564_111+0.098_78+16= 136.877 Cb= -0.148_197-0.291_111+0.439_78+128= 100.785 Cr = 0.439_197-0.368_111-0.071*78+128 = 168.097 由此可见，PIL中并非按照这个公式进行“RGB”到“YCbCr”的转换。

g 模式“I” 模式“I”为32位整型灰色图像，它的每个像素用32个bit表示，0表示黑，255表示白，(0,255)之间的数字表示不同的灰度。在PIL中，从模式“RGB”转换为“I”模式是按照下面的公式转换的： I = R * 299/1000 + G * 587/1000 + B * 114/1000

h 模式“F” 模式“F”为32位浮点灰色图像，它的每个像素用32个bit表示，0表示黑，255表示白，(0,255)之间的数字表示不同的灰度。在PIL中，从模式“RGB”转换为“F”模式是按照下面的公式转换的： F = R * 299/1000+ G * 587/1000 + B * 114/1000

图像保存

img.save('d:/lena.jpg')

注:后面的转化代码处理模式不一样，其余都是一样的，所以没有写代码

图像通道分离与合并

还是以lena.jpg图像为例，实现图像通道分离合并的操作

from PIL import Image
import numpy as np
import scipy
import matplotlib.pyplot as plt

img = Image.open('len.jpg')
print(img.mode)
print(img.getpixel((0, 0)))
gray = img.convert("L")
r, g, b = img.split()  # 分离三通道
pic = Image.merge('RGB', (r, g, b))  # 合并三通道
plt.figure("beauty")
plt.subplot(2, 3, 1), plt.title('origin')
plt.imshow(img), plt.axis('off')
plt.subplot(2, 3, 2), plt.title('gray')
plt.imshow(gray, cmap='gray'), plt.axis('off')
plt.subplot(2, 3, 3), plt.title('merge')
plt.imshow(pic), plt.axis('off')
plt.subplot(2, 3, 4), plt.title('r')
plt.imshow(r, cmap='gray'), plt.axis('off')
plt.subplot(2, 3, 5), plt.title('g')
plt.imshow(g, cmap='gray'), plt.axis('off')
plt.subplot(2, 3, 6), plt.title('b')
plt.imshow(b, cmap='gray'), plt.axis('off')
plt.show()

结果如图所示 ![ Python 图像处理（一）PIL ]

几何变换

Image类有resize()、rotate()和transpose()方法进行几何变换

1、图像的缩放和旋转

dst = img.resize((128, 128)) dst = img.rotate(45) # 顺时针角度表示
2、转换图像

dst = im.transpose(Image.FLIP_LEFT_RIGHT) #左右互换 dst = im.transpose(Image.FLIP_TOP_BOTTOM) #上下互换 dst = im.transpose(Image.ROTATE_90) #顺时针旋转 dst = im.transpose(Image.ROTATE_180) dst = im.transpose(Image.ROTATE_270)

图像矩阵变换

在文章上半部分中主要利用Image.open（）来打开一幅图像，然后直接对这个PIL对象进行操作。这种操作对于那些简单的图像操作还可以，但是如果需要对图像进行研究等复杂的操作则局限性很大。因此，通常我们加载完图片后，都是把图片转换成矩阵来进行更加复杂的操作。

打开图像并转换为矩阵

from PIL import Image import numpy as np import matplotlib.pyplot as plt img=np.array(Image.open('d:/lena.jpg')) #打开图像并转化为数组对象 print(img) #打印数组 print(img.shape) #大小 (512, 512, 3) print(img.dtype) # 类型 uint8 print(img.size) #图像大小 786432 plt.figure("lena") plt.imshow(img) plt.axis('off') plt.show()

如果是RGB图片，那么转换为array之后，就变成了一个rows_cols_channels的三维矩阵,因此，我们可以使用img[i,j,k]来访问像素值

例1：打开图片，并随机添加一些椒盐噪声

from PIL import Image import numpy as np import matplotlib.pyplot as plt

img = np.array(Image.open('len.jpg'))

随机生成5000个椒盐

rows, cols, dims = img.shape for i in range(5000): x = np.random.randint(0, rows) y = np.random.randint(0, cols) img[x, y, :] = 255 plt.figure("beauty") plt.imshow(img) plt.axis('off') plt.show()

结果如图： Python 图像处理（一）PIL

例2：将lena图像二值化，像素值大于128的变为1，否则变为0

from PIL import Image import numpy as np import matplotlib.pyplot as plt

img = np.array(Image.open('len.jpg').convert('L'))

rows, cols = img.shape for i in range(rows): for j in range(cols): if (img[i, j] <= 128): img[i, j] = 0 else: img[i, j] = 1 plt.figure("lena") plt.imshow(img, cmap='gray') plt.axis('off') plt.show()

结果如下图所示： Python 图像处理（一）PIL

如果要对多个像素点进行操作，可以使用数组切片方式访问。切片方式返回的是以指定间隔下标访问该数组的像素值。下面是有关灰度图像的一些例子：

img[i,:] = im[j,:] # 将第 j 行的数值赋值给第 i 行

img[:,i] = 100 # 将第 i 列的所有数值设为 100

img[:100,:50].sum() # 计算前 100 行、前 50 列所有数值的和

img[50:100,50:100] # 50~100 行，50~100 列（不包括第 100 行和第 100 列）

img[i].mean() # 第 i 行所有数值的平均值

img[:,-1] # 最后一列

img[-2,:] (or im[-2]) # 倒数第二行

直方图

一、画灰度图直方图

绘图都可以调用matplotlib.pyplot库来进行，其中的hist函数可以直接绘制直方图。

调用方式：
n, bins, patches = plt.hist(arr, bins=50, normed=1, facecolor='green', alpha=0.75)
hist的参数非常多，但常用的就这五个，只有第一个是必须的，后面四个可选

arr: 需要计算直方图的一维数组

bins: 直方图的柱数，可选项，默认为10

normed: 是否将得到的直方图向量归一化。默认为0

facecolor: 直方图颜色

alpha: 透明度

返回值 ：

n: 直方图向量，是否归一化由参数设定

bins: 返回各个bin的区间范围

patches: 返回每个bin里面包含的数据，是一个list


from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
img=np.array(Image.open('len.jpg').convert('L'))

plt.figure("lena")
arr=img.flatten()
n, bins, patches = plt.hist(arr, bins=256, normed=1, facecolor='green', alpha=0.75)
print(n)
print(bins)
print(patches)
plt.show()

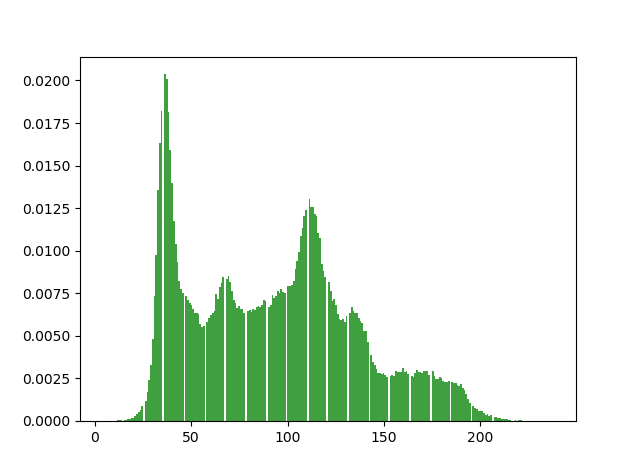
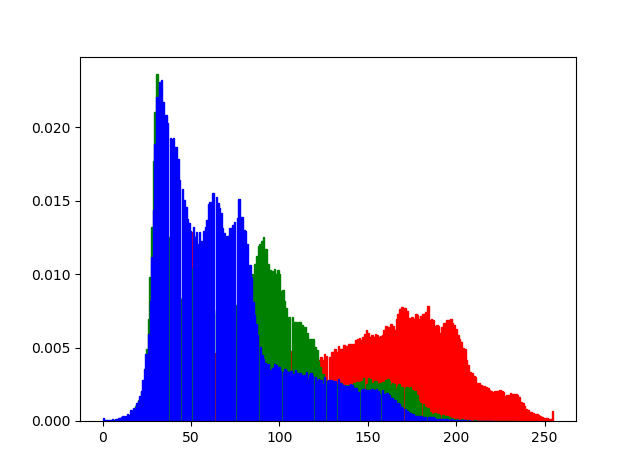
得到如下图所示： Python 图像处理（一）PIL

二、彩色图片直方图

实际上是和灰度直方图一样的，只是分别画出三通道的直方图，然后叠加在一起。

from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
src=Image.open('len.jpg')
r,g,b=src.split()

plt.figure("lena")
ar=np.array(r).flatten()
plt.hist(ar, bins=256, normed=1,facecolor='r',edgecolor='r',hold=1)
ag=np.array(g).flatten()
plt.hist(ag, bins=256, normed=1, facecolor='g',edgecolor='g',hold=1)
ab=np.array(b).flatten()
plt.hist(ab, bins=256, normed=1, facecolor='b',edgecolor='b')
plt.show()

如图： Python 图像处理（一）PIL